Uncovering Nature’s Equations with AI

by

Author: Denis Avetisyan

A new framework combines the reasoning power of large language models with physics principles to automatically derive interpretable equations from data.

The KeplerAgent leverages physics-based tools to autonomously discover equations from data, demonstrating an ability to distill underlying mathematical relationships from observed phenomena [latex] \implies [/latex] a capacity for generalized analytical reasoning.
The KeplerAgent leverages physics-based tools to autonomously discover equations from data, demonstrating an ability to distill underlying mathematical relationships from observed phenomena [latex] \implies [/latex] a capacity for generalized analytical reasoning.

KeplerAgent leverages symbolic regression and physics-informed machine learning to advance scientific equation discovery.

Discovering interpretable equations from data remains a central challenge in scientific modeling, yet current approaches often bypass the nuanced, multi-step reasoning process employed by physicists. In the work ‘Think like a Scientist: Physics-guided LLM Agent for Equation Discovery’, we introduce KeplerAgent, an agentic framework that explicitly mimics scientific reasoning by leveraging physics-based tools to extract structural information and guide symbolic regression. This approach substantially improves both the accuracy and robustness of equation discovery compared to traditional methods and existing large language model (LLM) baselines. Could this physics-guided approach unlock a new paradigm for scientific machine learning, enabling LLMs to not just find equations, but truly understand the underlying physical principles?

The Enduring Challenge of Equation Discovery

Historically, the process of uncovering the underlying mathematical relationships within data has been profoundly dependent on human expertise. Scientists would meticulously analyze data, leveraging their domain knowledge to select relevant variables – a process known as feature engineering – and then construct potential equations by hand. This approach, while yielding valuable insights, is inherently slow and susceptible to inaccuracies introduced by subjective choices or overlooked interactions. The reliance on manual feature engineering creates a bottleneck, particularly when dealing with high-dimensional datasets where the number of possible combinations of variables explodes, and subtle but crucial relationships might remain hidden. This traditional method struggles to scale with the ever-increasing volume and complexity of modern scientific data, limiting the speed of discovery and potentially biasing results towards pre-conceived notions.

The relentless growth of scientific datasets, generated by fields from genomics to astrophysics, presents a significant challenge to traditional methods of equation discovery. While symbolic regression – the automated search for mathematical expressions describing data – offers a potential solution, current techniques falter when faced with the complexity inherent in real-world systems. These algorithms often struggle with the ‘curse of dimensionality’, requiring exponentially more computational power as the number of potential terms and operators increases. Consequently, they become impractical for datasets with numerous variables or intricate relationships, frequently getting trapped in local optima or failing to converge on meaningful [latex] \text{equations} [/latex]. This limitation hinders progress in areas where rapid modeling and understanding of complex phenomena are crucial, necessitating the development of more scalable and robust symbolic regression approaches.

The inability to efficiently derive governing equations from data presents a significant bottleneck across numerous scientific fields. From climate modeling and materials science to drug discovery and astrophysics, complex systems are characterized by intricate relationships that demand precise mathematical representation. Current limitations in automated equation discovery slow the pace of innovation, hindering the ability to quickly test hypotheses, predict system behavior, and ultimately, gain deeper insights. This delay impacts not only fundamental research, but also practical applications reliant on accurate modeling – areas like optimizing energy grids, designing novel materials with specific properties, or forecasting disease outbreaks. The challenge, therefore, extends beyond a purely mathematical problem; it represents a critical impediment to accelerating scientific progress and addressing pressing global challenges.

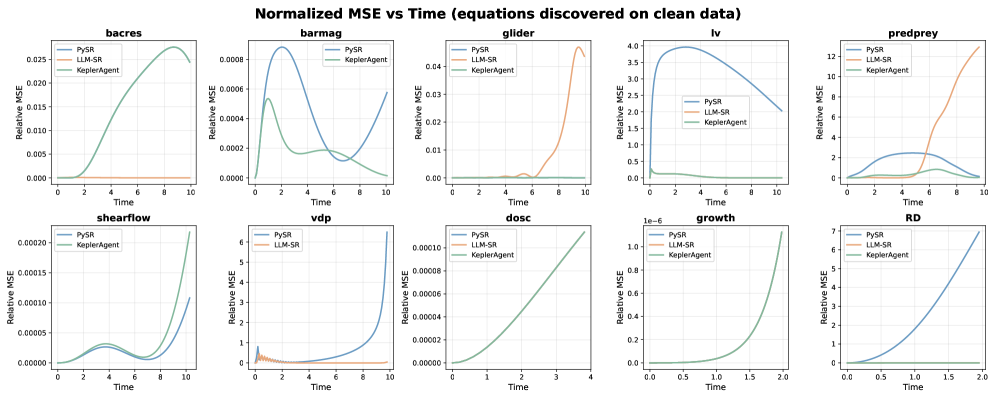
KeplerAgent successfully discovered governing equations-as measured by normalized mean squared error over time-for a wider range of scenarios than PySR or LLM-SR, which often failed to produce numerically stable simulations.
KeplerAgent successfully discovered governing equations-as measured by normalized mean squared error over time-for a wider range of scenarios than PySR or LLM-SR, which often failed to produce numerically stable simulations.

A Framework Guided by Logical Necessity

KeplerAgent implements a framework integrating physics-based tools, symbolic regression, and a Large Language Model (LLM) for automated equation discovery. The LLM functions as a central orchestrator, interpreting problem descriptions and directing the selection and configuration of appropriate tools such as numerical solvers and simulation engines. Symbolic regression algorithms are then employed to derive candidate equations from data generated by these tools. This integration allows KeplerAgent to move beyond traditional symbolic regression by leveraging the strengths of both simulation and analytical methods, enabling it to tackle more complex problems and discover equations that accurately reflect underlying physical principles.

KeplerAgent employs an LLM to automate tool selection and configuration within the equation discovery pipeline. The LLM analyzes the given data and problem description to determine the optimal sequence of physics-informed tools – including those for data preprocessing, feature engineering, and symbolic regression – and configures their parameters accordingly. This automated orchestration minimizes the requirement for human-specified tool chains and parameter tuning, significantly reducing manual effort and the potential for subjective bias in the equation discovery process. The LLM dynamically adjusts the tool configuration based on intermediate results, enabling an iterative refinement of the equation search and improving overall efficiency.

KeplerAgent leverages prior physical knowledge to significantly reduce the complexity of equation discovery. Instead of exhaustively searching the entire space of possible equations, the framework incorporates known physical constraints and relationships – such as dimensional analysis and expected functional forms – to limit the search to plausible candidates. This constraint effectively narrows the hypothesis space, improving the efficiency of symbolic regression and other equation discovery tools. Consequently, the incorporation of prior knowledge not only accelerates the process but also enhances the accuracy of discovered equations by reducing the likelihood of identifying spurious correlations or physically unrealistic models. The system’s ability to prioritize physically meaningful solutions is a key differentiator in scenarios with limited or noisy data.

Our KeplerAgent framework iteratively reasons about dataset information, tool specifications, and prior steps to discover equations, guided by a system prompt and maintained within a workspace and experience log.
Our KeplerAgent framework iteratively reasons about dataset information, tool specifications, and prior steps to discover equations, guided by a system prompt and maintained within a workspace and experience log.

Symmetry: A Principle of Parsimony

The Symmetry Discovery module within the framework functions by analyzing the input data to identify inherent symmetries, such as invariance under transformations like time reversal or spatial reflection. These symmetries are then expressed as constraints on the form of potential equations. For example, if a system exhibits symmetry with respect to a variable [latex]x[/latex], any discovered equation must remain valid when [latex]x[/latex] is replaced with its negative. By incorporating these constraints, the number of candidate equations requiring evaluation during the search process is substantially reduced, as equations violating the identified symmetries are automatically excluded. This approach is particularly effective in systems governed by physical laws, where symmetries are common and can dramatically accelerate equation discovery.

Symmetry constraints operate by reducing the dimensionality of the search space during equation discovery. This pruning is achieved by identifying and eliminating redundant equation forms that, due to the identified symmetries, will yield identical predictions. For example, if a system exhibits symmetry with respect to a variable [latex]x[/latex], an equation involving [latex]x^2[/latex] is structurally equivalent to one involving [latex](-x)^2[/latex], effectively halving the number of equations needing evaluation. This reduction in complexity directly translates to decreased computational cost and faster convergence towards accurate governing equations, particularly in high-dimensional systems where the number of potential equations grows exponentially with the number of independent variables.

The framework leverages the capabilities of PySINDy and PySR to perform efficient equation discovery within the reduced search space created by symmetry analysis. PySINDy utilizes Sparse Regression techniques, employing algorithms like Sequential Threshold Least Squares to identify the fewest terms necessary to accurately model the system dynamics, prioritizing parsimony and interpretability. PySR, conversely, implements Genetic Programming, evolving candidate equations through selection and mutation to optimize their fit to the data. Both tools benefit from the dimensionality reduction achieved through symmetry constraints, significantly decreasing computational cost and enabling the exploration of more complex equation forms that would otherwise be intractable. The integration allows for a complementary approach, combining the strengths of both sparse regression and symbolic regression for robust and efficient equation discovery.

KeplerAgent achieves the lowest normalized mean squared error [latex]MSE[/latex] over time when identifying equations from noisy data, outperforming both PySR and LLM-SR.
KeplerAgent achieves the lowest normalized mean squared error [latex]MSE[/latex] over time when identifying equations from noisy data, outperforming both PySR and LLM-SR.

Validation and the Pursuit of Truth

Rigorous validation of the derived equations is paramount to ensuring the models genuinely reflect the governing physical principles. This process utilizes established measures of numerical accuracy, assessing how closely the solutions generated by the equations align with expected behaviors and known physical constraints. Beyond simply achieving a solution, the focus is on fidelity – guaranteeing that the mathematical representation accurately captures the underlying phenomena, even under varying conditions or with complex interactions. Such validation isn’t merely a quality check; it’s foundational to building trust in the model’s predictive power and its utility in scientific exploration, allowing researchers to confidently extrapolate results and gain deeper insights into the systems being studied. The equations are tested against a range of scenarios, and any discrepancies are carefully analyzed to refine the model and improve its representation of reality.

KeplerAgent demonstrates a significant advancement in symbolic regression, achieving 45% accuracy on challenging differential equation (DiffEq) datasets. This performance surpasses that of established baseline methods within the DiffEq benchmark, indicating a heightened capacity to rediscover the underlying mathematical relationships governing dynamic systems. The system’s success isn’t merely about finding a solution, but rather identifying the correct symbolic expression with a considerably higher probability than current approaches. This improved accuracy is crucial for scientific discovery, allowing researchers to move beyond numerical approximations and gain deeper, more interpretable insights into the physical processes being modeled, potentially accelerating progress in fields reliant on differential equation modeling.

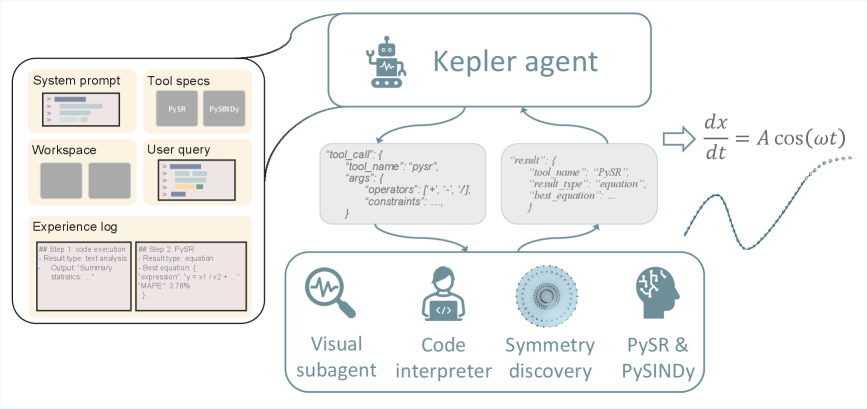
KeplerAgent demonstrates a notable resilience to real-world data imperfections, consistently achieving top performance – either the best or near-best results – across 6 out of 10 tested dynamical systems when confronted with noisy data. This robustness suggests the model isn’t simply memorizing training examples, but rather learning the underlying principles governing the system’s behavior. The ability to accurately model systems even with imperfect inputs is critical for practical applications, as truly clean datasets are rare, and this performance metric highlights KeplerAgent’s potential for reliable predictions in complex, uncertain environments. This finding underscores the model’s advanced capacity to generalize beyond the limitations of pristine data and deliver consistent, accurate results in more realistic scenarios.

KeplerAgent demonstrates a marked improvement in precision when applied to clean datasets, as evidenced by a lower normalized Mean Squared Error (MSE) compared to established symbolic regression methods like PySR and Large Language Model Symbolic Regression (LLM-SR). This metric quantifies the average squared difference between KeplerAgent’s predicted equations and the true underlying functions, with a lower value indicating a closer approximation. The observed reduction in normalized MSE suggests that KeplerAgent not only identifies functional relationships but does so with greater fidelity, minimizing the error between its symbolic representations and the actual data generating process – a crucial characteristic for reliable modeling and prediction in scientific applications.

Across a suite of differential equation problems, PySR, LLM-SR, and KeplerAgent exhibit varying performance as measured by normalized mean squared error ([latex]NMSE[/latex]), with median values indicating the central tendency of each approach.
Across a suite of differential equation problems, PySR, LLM-SR, and KeplerAgent exhibit varying performance as measured by normalized mean squared error ([latex]NMSE[/latex]), with median values indicating the central tendency of each approach.

KeplerAgent, as detailed in the study, prioritizes the derivation of equations grounded in established physical principles. This echoes the sentiment expressed by Paul Erdős: “A mathematician knows a lot of things, but a good mathematician knows which ones to use.” The framework doesn’t merely seek correlations within data; it actively incorporates physics-based constraints and symmetry detection – effectively ‘choosing which things to use’ – to arrive at solutions possessing both accuracy and interpretability. This focus on provable, physics-informed solutions, rather than simply ‘working’ equations, aligns with a rigorous mathematical approach where correctness, not just empirical success, is paramount. The agent’s ability to navigate the solution space guided by these principles represents a significant step towards truly scientific machine learning.

Beyond the Curve

The pursuit of equation discovery, as exemplified by KeplerAgent, ultimately reveals a fundamental tension. The framework demonstrably improves upon existing methods, yet remains tethered to the quality of the underlying symbolic regression tools. A truly elegant solution would not merely find an equation that fits, but derive it from first principles, guided by inherent symmetries and conservation laws. Current approaches, even those informed by physics, are largely pattern-matching exercises – sophisticated, certainly, but lacking the deductive power of mathematical proof.

Future work must address this limitation. The focus should shift from merely representing observed data to constructing models that are demonstrably consistent with established physical constraints. This requires a deeper integration of formal methods and a willingness to abandon purely data-driven approaches when they yield logically inconsistent results. The question is not whether an LLM can discover an equation, but whether it can participate in a rigorous, provable derivation.

Symmetry detection, while promising, remains a largely heuristic endeavor. A truly robust system would automatically identify and exploit the underlying symmetries of a problem, reducing the search space and ensuring the resulting equations possess the expected invariances. Until such a system is realized, the search for elegant, physically meaningful equations will remain, at best, an approximation of genuine understanding.

Original article: https://arxiv.org/pdf/2602.12259.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-13 08:53