Unlocking PDE Families: A New Approach to Analytical Solutions

by

Author: Denis Avetisyan

Researchers have developed a multitasking neuro-symbolic framework that efficiently discovers shared mathematical structures within partial differential equation families, leading to more accurate and generalizable solutions.

Current approaches to solving partial differential equations-whether through physics-informed neural networks, neural operators, or symbolic regression-each sacrifice either generalizability, interpretability, or the ability to address multiple problems concurrently, whereas a novel method seeks to overcome these limitations by constructing a unified search space and enabling knowledge transfer between tasks, ultimately yielding solutions that are both adaptable and analytically transparent.
Current approaches to solving partial differential equations-whether through physics-informed neural networks, neural operators, or symbolic regression-each sacrifice either generalizability, interpretability, or the ability to address multiple problems concurrently, whereas a novel method seeks to overcome these limitations by constructing a unified search space and enabling knowledge transfer between tasks, ultimately yielding solutions that are both adaptable and analytically transparent.

This work introduces a novel framework for PDE solving that combines symbolic regression, physics-informed learning, and an affine transformation mechanism to enhance both interpretability and performance.

Solving families of Partial Differential Equations (PDEs) presents a significant challenge due to the computational cost of independently addressing each instance, while existing machine learning approaches often lack the interpretability of analytical solutions. This work, ‘Neuro-Symbolic Multitasking: A Unified Framework for Discovering Generalizable Solutions to PDE Families’, introduces a novel framework, NMIPS, that leverages shared mathematical structures and an affine transfer method to simultaneously discover interpretable analytical solutions across PDE families. By effectively multitasking and transferring learned knowledge, NMIPS achieves improved accuracy-up to a [latex]35.7\%[/latex] increase-compared to existing methods. Could this neuro-symbolic approach unlock a new paradigm for both efficient and insightful PDE solving across diverse scientific and engineering domains?

The Inevitable Bottleneck: Why PDEs Resist Computation

The ability to model and predict physical phenomena across diverse fields – from fluid dynamics and heat transfer to electromagnetism and quantum mechanics – hinges on solving Partial Differential Equations [latex]\text{PDEs}[/latex]. However, despite decades of advancement, obtaining solutions to these equations often presents a significant computational bottleneck. The inherent complexity of [latex]\text{PDEs}[/latex], particularly when dealing with realistic geometries or multiple interacting physical processes, demands immense processing power and time. Traditional numerical techniques, while reliable, frequently require discretizing the problem into millions – or even billions – of smaller elements, leading to substantial memory requirements and lengthy simulation times. This computational burden restricts the scope of investigations, limits the accuracy of predictions, and hinders the ability to explore parameter spaces effectively, ultimately slowing progress in numerous scientific and engineering endeavors.

The application of established numerical techniques, such as Finite Element and Finite Volume methods, to solve complex physical models often encounters substantial computational limitations. These methods discretize the continuous domain into a mesh of elements or volumes, requiring extensive calculations at each point to approximate the solution to the [latex]\partial\phi/\partial t = \nabla \cdot D[/latex] equation. The computational cost scales rapidly with the number of elements, meaning that refining the mesh to improve accuracy – particularly when dealing with intricate geometries or problems involving multiple interacting physical phenomena – demands ever-increasing processing power and memory. This resource intensity restricts the size and complexity of simulations, hindering the ability to model real-world systems with sufficient detail and ultimately presenting a significant bottleneck in many scientific and engineering investigations.

The pursuit of analytical solutions to Partial Differential Equations (PDEs) frequently encounters significant obstacles, effectively restricting comprehensive understanding and predictive modeling of complex systems. While analytical solutions offer exact, insightful representations of a system’s behavior – unlike the approximations inherent in numerical methods – their derivation proves exceedingly difficult, if not impossible, for all but the simplest equations. This intractability stems from the nonlinearities often present in real-world phenomena and the intricate boundary conditions required to accurately represent physical constraints. Consequently, researchers often rely on computationally intensive numerical simulations, sacrificing precision for feasibility, or are forced to make simplifying assumptions that limit the scope and accuracy of their predictions. The inability to obtain closed-form solutions therefore represents a fundamental bottleneck in fields ranging from fluid dynamics and heat transfer to quantum mechanics and financial modeling, hindering both scientific discovery and technological advancement.

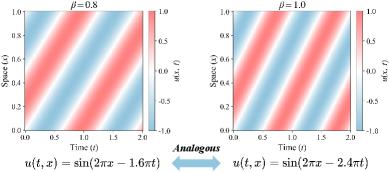
Numerical solutions of partial differential equations show that equations within the same family consistently yield similar analytical solutions.
Numerical solutions of partial differential equations show that equations within the same family consistently yield similar analytical solutions.

Recovering the Signal: Symbolic Regression as Archeology of Equations

Symbolic Regression distinguishes itself from traditional regression techniques by directly seeking mathematical equations that best represent the relationship within a dataset, rather than optimizing parameters within a pre-defined model. This is accomplished through evolutionary algorithms, typically genetic programming, which iteratively refine candidate expressions – composed of mathematical operators and variables – based on their goodness-of-fit to the observed data. The resulting models are not limited by assumptions about functional form, and can potentially uncover underlying analytical relationships expressed as [latex]f(x) = ax^2 + bsin(x)[/latex] or other interpretable equations, offering insights beyond simple predictive accuracy. Unlike black-box models, the output of Symbolic Regression is a mathematical expression directly usable for analysis, simulation, and extrapolation.

Standard Symbolic Regression methods face significant computational challenges when applied to real-world Partial Differential Equations (PDEs). The search space for potential mathematical expressions grows exponentially with the number of variables, terms, and operators considered, leading to combinatorial explosion. This is particularly acute with PDEs, which often require complex, multi-dimensional functions to accurately model physical phenomena. Consequently, even moderately complex PDEs can demand substantial computational resources – processing time and memory – making exhaustive searches impractical. Furthermore, the lack of gradient information in symbolic regression necessitates evaluating a large number of candidate equations, further exacerbating the computational burden and limiting scalability to higher-dimensional problems or datasets with significant noise.

Genetic Programming Symbolic Regression (GP-SR) utilizes evolutionary algorithms to explore the space of possible mathematical expressions, iteratively refining candidate solutions based on their fit to observed data. This approach employs techniques like genetic crossover and mutation to generate new expressions, providing a robust method for navigating complex search landscapes where traditional optimization methods may fail. However, GP-SR typically requires substantial computational resources and often produces models that are highly specific to the training data. Consequently, generalization to slightly altered problem instances or datasets with different characteristics remains a significant limitation, necessitating retraining or significant parameter adjustments for each new application. The resulting models frequently lack the adaptability seen in more generalized analytical solutions.

The Family Resemblance: Multitasking Symbolic Regression as Evolutionary Advantage

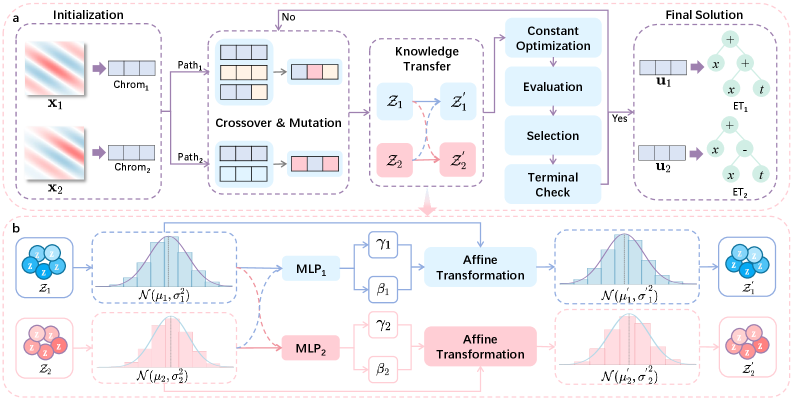
Multitasking Symbolic Regression (MSR) is a novel framework designed to concurrently solve multiple Partial Differential Equations (PDEs) that belong to the same mathematical family. This is accomplished by recognizing and exploiting the inherent structural similarities between equations within the family, rather than treating each PDE as an isolated problem. By simultaneously optimizing for all equations, MSR facilitates knowledge transfer, allowing solutions discovered for one PDE to inform and accelerate the discovery of solutions for related PDEs. This approach differs from traditional methods which typically solve each PDE independently, leading to redundant computation and a failure to capitalize on shared mathematical properties. The core principle is that solving a family of PDEs together can be more efficient and effective than solving them in isolation.

Multifactorial Optimization and Affine Transfer facilitate knowledge transfer between related problems within the Multitasking Symbolic Regression framework. Multifactorial Optimization simultaneously optimizes the expression tree for multiple Partial Differential Equations (PDEs) by considering their collective error, enabling the identification of shared mathematical structures. Affine Transfer then leverages these identified structures by applying learned components – specifically, sub-trees within the expression tree – from one PDE to another. This process involves scaling and shifting these sub-trees to adapt to the specific parameters and boundary conditions of the target PDE, thereby accelerating the search for accurate solutions and improving generalization performance across the PDE family.

The framework utilizes an Expression Tree representation to encode analytical solutions for each Partial Differential Equation (PDE) within a family. These trees recursively define mathematical operations – including addition, subtraction, multiplication, division, and various functions – applied to input variables and constants. This structure allows for the explicit representation of the mathematical form of the solution, facilitating knowledge transfer between related PDEs. By identifying shared subtrees – representing common mathematical components – across different PDEs within the family, the system can leverage previously discovered solutions to accelerate learning and improve generalization performance on new instances. The Expression Tree’s hierarchical structure also enables efficient exploration of the solution space and facilitates the creation of interpretable models, where the mathematical form of the solution is directly accessible.

The proposed Multitasking Symbolic Regression framework was evaluated on six benchmark partial differential equations (PDEs): 1D Burgers’ Equation, 1D Advection-Diffusion Equation, 2D Advection Equation, 2D Navier-Stokes Equation, 1D Advection Equation, and 3D Advection Equation. Across these diverse PDEs, the method achieved an average Mean Squared Error (MSE) of 1.19E-01, indicating a consistent level of accuracy in discovering analytical solutions. This performance demonstrates the framework’s capacity to generalize and effectively address a range of problems within the PDE domain, offering both accurate and interpretable results.

Performance evaluations demonstrate that the Multitasking Symbolic Regression framework achieves a 17.6% reduction in mean squared error (MSE) when applied to the 2D Advection equation, relative to the highest-performing baseline method under identical conditions. Furthermore, computational speedups of up to one order of magnitude were observed across the tested PDE family, indicating a significant efficiency gain. These improvements are attributed to the framework’s ability to leverage shared mathematical structure and transfer knowledge between related problems, reducing the computational resources required to discover accurate solutions.

The proposed NMIPS framework leverages a multifactorial PDE solving approach with affine transformation-based knowledge transfer-using multi-layer perceptrons to learn scaling and shifting parameters from population statistics-to efficiently solve multiple tasks within a PDE family.
The proposed NMIPS framework leverages a multifactorial PDE solving approach with affine transformation-based knowledge transfer-using multi-layer perceptrons to learn scaling and shifting parameters from population statistics-to efficiently solve multiple tasks within a PDE family.

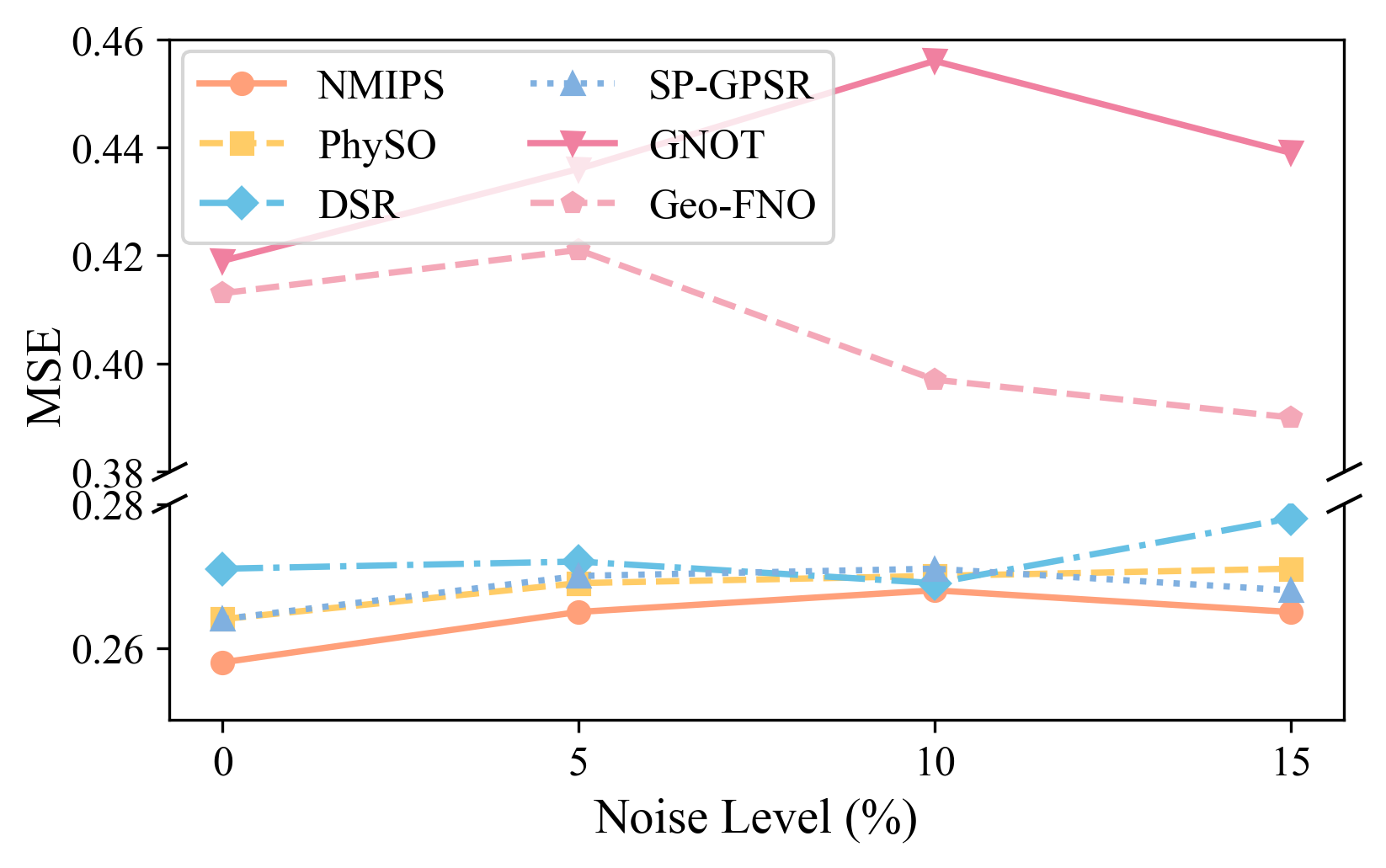
Beyond Prediction: Robustness and the Future of Symbolic PDE Solutions

The Multitasking Symbolic Regression framework exhibits a remarkable capacity to maintain solution accuracy even when confronted with noisy data. Testing revealed consistently low Mean Squared Error (MSE) values – a key indicator of predictive power – persisted even with the addition of up to 15% Gaussian noise. This resilience stems from the framework’s ability to simultaneously learn multiple related tasks, effectively averaging out the impact of individual data errors and converging on the underlying [latex]PDE[/latex] solution. Such robustness is particularly valuable in real-world scientific and engineering applications where data acquisition is often imperfect or subject to experimental uncertainties, and allows for reliable [latex]PDE[/latex] solutions even in the presence of significant data imperfections.

The Multitasking Symbolic Regression framework offers a distinct advantage in real-world applications frequently hampered by imperfect data. Unlike many PDE solution methods that demand high-fidelity datasets, this approach exhibits notable robustness against noise, consistently achieving low mean squared error even with significant data corruption. Crucially, this resilience isn’t achieved at the cost of understanding; the framework delivers not merely numerical approximations, but interpretable analytical solutions – [latex]f(x,t) = …[/latex] – offering valuable physical insight. This combination of accuracy and clarity makes it particularly well-suited for fields like environmental modeling, materials science, and medical imaging, where data acquisition is often expensive, prone to error, or incomplete, allowing researchers to confidently extract meaningful results even from challenging datasets.

The Multifaceted Symbolic Regression framework’s development is poised to address increasingly challenging problems in computational science. Future investigations will prioritize expanding the framework’s capabilities to encompass a wider array of partial differential equation (PDE) families, moving beyond current limitations. Crucially, researchers intend to explore synergistic integrations with cutting-edge machine learning techniques, specifically Physics-Informed Neural Networks (PINNs) and Neural Operators. This convergence aims to leverage the strengths of both symbolic regression – its capacity for deriving interpretable analytical solutions – and neural networks – their prowess in handling high-dimensional data and complex, nonlinear relationships. Such hybrid approaches promise not only to bolster the accuracy and efficiency of PDE solutions but also to significantly improve generalization capabilities, allowing for robust predictions even with limited or noisy data, and ultimately accelerating scientific discovery and engineering innovation across diverse fields.

The capacity to efficiently and accurately solve partial differential equations (PDEs) stands to revolutionize diverse fields, and this work presents a methodology poised to accelerate that progress. By offering a means to not only obtain solutions but also to express them in readily interpretable analytical forms, researchers gain deeper insights into the underlying phenomena modeled by these equations. This capability extends beyond mere prediction; it enables the formulation of new hypotheses, the refinement of existing theories, and ultimately, the potential for groundbreaking discoveries in areas ranging from fluid dynamics and materials science to financial modeling and climate prediction. The combination of robustness to noisy data and the delivery of symbolic solutions positions this approach as a valuable tool for both scientific advancement and the development of innovative engineering applications, promising a future where complex physical systems can be understood and controlled with greater precision.

Different methods exhibit varying robustness to noise, with some demonstrating significantly better performance in noisy conditions than others.
Different methods exhibit varying robustness to noise, with some demonstrating significantly better performance in noisy conditions than others.

The pursuit of generalized solutions, as demonstrated by this work on neuro-symbolic multitasking, reveals a fundamental truth about complex systems. It isn’t merely about achieving accurate results, but about uncovering the underlying mathematical invariants that govern those results. As Vinton Cerf observed, “Any sufficiently advanced technology is indistinguishable from magic.” This research echoes that sentiment; by bridging the gap between data-driven learning and symbolic reasoning, the framework doesn’t simply solve partial differential equations-it begins to reveal the elegant, almost magical, order inherent within them. Monitoring the transfer mechanism’s performance, in particular, becomes the art of fearing consciously, anticipating where the shared structures will hold and where the system will inevitably reveal its limitations.

What Lies Ahead?

This work, in its pursuit of analytical solutions through a multitasking framework, has predictably revealed the limits of analytical solutions. The achieved gains in efficiency and generalization are not destinations, but invitations to more complex failures. A system that reliably discovers solutions to partial differential equations is, in effect, a system primed to encounter those equations it cannot solve. The very act of codifying shared mathematical structures-of attempting to anticipate the landscape of possible PDEs-creates a boundary beyond which the framework will inevitably stumble.

Future iterations will undoubtedly focus on expanding the scope of ‘families’ amenable to this approach. However, the true challenge lies not in breadth, but in embracing the inherent messiness of the physical world. The insistence on interpretable, analytical forms-while laudable-may ultimately prove a constraint. Perhaps the most fruitful path forward involves relinquishing some degree of interpretability, allowing the system to explore solutions that are accurate, but opaque-acknowledging that perfection leaves no room for people.

The current emphasis on affine transformations, while effective, represents a specific bias within the larger space of possible mappings. To truly grow this ecosystem, future work must explore mechanisms for discovering-or, more accurately, allowing to emerge-novel transformation rules, accepting that each new rule will, in time, reveal its own inherent limitations.

Original article: https://arxiv.org/pdf/2602.11630.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-15 21:10