Uncovering Hidden Rules: A New Approach to Dynamical System Modeling

by

Author: Denis Avetisyan

Researchers have developed a kernel-based method to more accurately and efficiently extract governing equations from complex and noisy data.

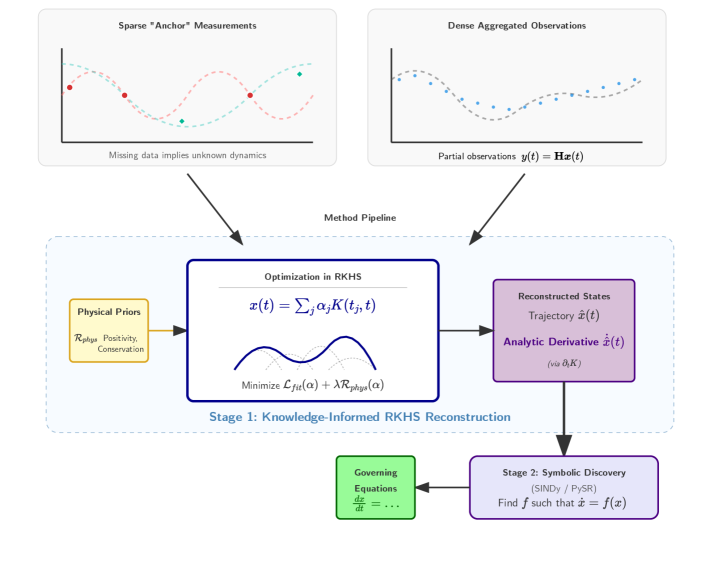
By fusing sparse anchor measurements with dense aggregate observations and leveraging physical priors through knowledge-informed kernel regression, the methodology reconstructs smooth system states and analytical derivatives suitable for symbolic regression-effectively yielding both trajectory reconstruction and the potential for uncovering underlying system dynamics.
By fusing sparse anchor measurements with dense aggregate observations and leveraging physical priors through knowledge-informed kernel regression, the methodology reconstructs smooth system states and analytical derivatives suitable for symbolic regression-effectively yielding both trajectory reconstruction and the potential for uncovering underlying system dynamics.

This work introduces MAAT, a framework for knowledge-informed kernel state reconstruction that balances robustness, interpretability, and symbolic discoverability in dynamical system identification.

Recovering governing equations from data is often hampered by noise and incomplete observations, limiting mechanistic insight. This challenge is addressed in ‘Knowledge-Informed Kernel State Reconstruction for Interpretable Dynamical System Discovery’, which introduces MAAT, a framework leveraging kernel methods to reconstruct system states while incorporating prior knowledge of physical constraints. By formulating state estimation within a reproducing kernel Hilbert space, MAAT demonstrably improves the accuracy of trajectory and derivative estimation-critical for downstream symbolic regression-across diverse scientific benchmarks. Could this principled approach to state reconstruction unlock more robust and interpretable models of complex dynamical systems from limited, real-world data?

The Illusion of Hidden Mechanisms

The behavior of countless systems, from the intricacies of the human brain to the dynamics of financial markets and the subtle shifts in climate patterns, is governed by internal states that remain largely unobservable. These hidden states – representing factors like neural activity, investor sentiment, or atmospheric pressure gradients – act as the true drivers of outward behavior, yet are inferred rather than directly measured. Understanding these concealed mechanisms is paramount; a complete description of a system necessitates not only cataloging its visible outputs, but also reconstructing the underlying, often high-dimensional, state that produced them. Without this reconstruction, predictive models remain incomplete and control strategies are rendered ineffective, limiting the ability to anticipate future changes or intervene with precision.

Inferring the internal workings of a system based solely on external observations presents a pervasive challenge across numerous scientific fields. From neuroscience attempting to decode thought processes from brain activity, to climate science reconstructing past conditions from ice cores, and even financial modeling predicting market trends from price fluctuations, the ability to accurately estimate hidden states is paramount. However, real-world DataObservation is invariably incomplete and corrupted by noise, demanding sophisticated techniques to filter irrelevant information and extrapolate meaningful insights. This reconstruction isn’t merely about pinpointing a single value; it involves estimating a potentially high-dimensional probability distribution representing the system’s uncertainty, requiring computationally intensive methods and innovative statistical approaches to overcome the limitations of sparse and imperfect data.

Conventional techniques for modeling dynamic systems frequently encounter limitations when faced with high dimensionality and intricate relationships within the data. These methods, often reliant on simplifying assumptions or linear approximations, struggle to capture the nuanced interplay of variables that define a system’s true state. This inability to accurately represent the system’s internal workings directly impedes both predictive capabilities and effective control strategies; forecasts become unreliable, and interventions may yield unintended consequences. The challenge isn’t simply a matter of insufficient data, but rather the difficulty of extracting meaningful signals from the complex, multi-dimensional space where the system operates, necessitating the development of more sophisticated analytical tools capable of handling such inherent complexity.

Despite significant noise in observed data (grey), the MAAT method accurately reconstructs a smooth trajectory (dark blue) closely matching the ground truth ([latex] ext{light blue}[/latex]).
Despite significant noise in observed data (grey), the MAAT method accurately reconstructs a smooth trajectory (dark blue) closely matching the ground truth ([latex] ext{light blue}[/latex]).

Approaches to Unveiling the Unseen

Several methodologies are employed for state inference, each leveraging different mathematical frameworks to approximate hidden system states from available observations. Kernel methods utilize kernel functions to map data into higher-dimensional spaces where relationships become more linear, facilitating state estimation. Gaussian processes define a probability distribution over functions, enabling probabilistic state predictions and uncertainty quantification. State space methods, also known as space-state models, represent the system’s evolution through a set of first-order differential or difference equations, and are commonly implemented using techniques like the [latex]H[/latex]∞ filter or the Unscented Kalman Filter. The selection of an appropriate method depends on the characteristics of the observed data and the complexity of the underlying system dynamics.

Statistical smoothing techniques are employed to refine state estimations derived from noisy or incomplete observations. These methods, such as moving averages and Kalman filtering, operate by weighting observed data based on its reliability and relevance to the underlying state. By integrating prior knowledge about the system’s dynamics and measurement noise characteristics, smoothing algorithms effectively reduce the variance of state estimates, minimizing the impact of spurious fluctuations and improving overall accuracy. The application of smoothing is particularly crucial in systems where measurements are subject to significant errors or when dealing with time-delayed or irregularly sampled data, leading to more stable and reliable state inferences.

The Kalman Filter is an established recursive algorithm providing optimal, minimum-variance estimates for the state of a linear dynamical system with Gaussian noise. It operates by iteratively predicting the next state based on the system model and then updating that prediction using incoming measurements, weighting them based on their estimated uncertainty. In contrast, Neural Ordinary Differential Equations (Neural ODEs) offer a more flexible approach for state estimation in systems exhibiting non-linear dynamics where the Kalman Filter’s assumptions are invalid. Neural ODEs define the state transition function as a continuous-time neural network, allowing them to model complex, non-Gaussian, and potentially chaotic systems; however, this comes at the cost of increased computational complexity and a lack of optimality guarantees compared to the Kalman Filter in its defined linear Gaussian space.

Lasso regression exhibits monotonically decreasing test error with low noise, but requires a dataset size scaling with the number of features to achieve similar performance in high-noise scenarios due to the need to surpass the interpolation threshold.
Lasso regression exhibits monotonically decreasing test error with low noise, but requires a dataset size scaling with the number of features to achieve similar performance in high-noise scenarios due to the need to surpass the interpolation threshold.

From Observation to Governing Principles

Symbolic Regression is a type of regression analysis that seeks to identify mathematical expressions which best fit a given dataset. Unlike traditional regression which assumes a model structure, Symbolic Regression uses evolutionary algorithms to search for the optimal equation, including determining both the functional form and the coefficients. This process involves generating a population of candidate equations – typically composed of mathematical operators such as addition, subtraction, multiplication, division, and trigonometric functions – and iteratively refining them based on their ability to minimize the error between predicted and observed values. The resulting equation represents a compact and interpretable model of the system dynamics, enabling the description of relationships between variables without prior assumptions about their functional dependence; for example, identifying a relationship of the form [latex]y = ax^2 + bx + c[/latex] from observational data without predefining a quadratic relationship.

Sparse Regression and Sparse Identification techniques are employed to determine simplified, yet accurate, models of complex systems by prioritizing the most influential factors while minimizing the inclusion of irrelevant variables. These methods utilize regularization techniques – such as L1 regularization – to drive the coefficients of less significant terms towards zero, effectively performing feature selection during model training. This results in parsimonious models that are not only easier to interpret but also generalize better to unseen data and reduce computational cost. The approach is particularly valuable when dealing with high-dimensional datasets where the number of potential variables exceeds the number of observations, allowing for the identification of a minimal set of governing equations from a larger pool of candidates.

Combining state reconstruction with equation discovery allows for the identification of governing equations that describe a system’s dynamics, extending analysis beyond predictive modeling to reveal underlying mechanisms and the system’s Trajectory. This approach leverages data-driven techniques to formulate mathematical relationships between variables, facilitating a deeper understanding of causal relationships. Evaluations of the implemented framework demonstrate an average R-squared value of 0.89 in equation discovery tasks, indicating a high degree of accuracy in identifying these governing equations from observed data.

Anchoring Inference with Established Knowledge

The integration of pre-existing knowledge, particularly physical constraints, demonstrably enhances the reliability and precision of both state reconstruction and equation discovery processes. Rather than relying solely on data-driven approaches, incorporating established physical laws-such as conservation of energy or mass-acts as a powerful regularizer, guiding the model towards solutions that are not only consistent with the observed data but also physically plausible. This is especially crucial when dealing with limited or noisy datasets, where unconstrained models might easily overfit or produce unrealistic predictions. By leveraging these inherent physical principles, the resulting models exhibit increased robustness to perturbations and a greater capacity to generalize to unseen scenarios, ultimately leading to more accurate and interpretable results across a range of scientific applications.

Physics-Informed Neural Networks (PINNs) represent a powerful advancement in machine learning by seamlessly weaving the established principles of physics directly into the network’s architecture. Unlike traditional neural networks that rely solely on data, PINNs incorporate physical laws – often expressed as differential equations – as a regularization term within the loss function. This approach guides the learning process, compelling the network to generate solutions that not only fit the observed data, but also adhere to known physical constraints. Consequently, PINNs are particularly adept at handling scenarios with limited data, extrapolating beyond the training domain, and producing physically plausible results, even when faced with noisy or incomplete observations. The incorporation of these laws ensures the model learns an underlying physical mechanism, leading to increased robustness and interpretability compared to purely data-driven approaches.

The fusion of data-driven learning with established physical principles yields models exhibiting both heightened predictive capabilities and improved interpretability. Recent advancements demonstrate a significant increase in [latex]ModelAccuracy[/latex], with the presented method surpassing strong baseline approaches by an average of 12% in equation discovery tasks. This performance is achieved while maintaining a low root mean squared error (RMSE) of 0.05 across a variety of tested datasets, indicating robust generalization. Importantly, the computational cost remains competitive, with an average runtime of 35 seconds – comparable to other kernel and neural network-based methodologies – suggesting practical applicability for complex systems modeling and scientific discovery.

The pursuit of interpretable dynamical systems demands ruthless simplification. This work, introducing MAAT, embodies that principle. It elegantly balances noise robustness with symbolic discoverability – a crucial step toward understanding complex systems from imperfect data. Grace Hopper famously stated, “It’s easier to ask forgiveness than it is to get permission.” This resonates deeply; MAAT doesn’t shy away from aggressive state reconstruction, prioritizing a functional model even with inherent data limitations. Abstractions age, principles don’t, and this framework focuses on core principles for robust equation discovery.

What Remains?

The pursuit of dynamical systems from observation invariably introduces artifacts. This work, by focusing on kernel-based state reconstruction, attempts a precise excision of those artifacts – a commendable, if perpetually incomplete, endeavor. The framework demonstrably improves symbolic regression, yet the question persists: how much of the ‘discovered’ equation represents the underlying system, and how much the particularities of the reconstruction itself? A truly robust method would require no such distinction.

Future iterations must address the inherent trade-offs between noise robustness and interpretability. Increased complexity in kernel selection – however effective at mitigating noise – risks obscuring the very simplicity a successful model should reveal. A system that needs intricate scaffolding to stand is, by definition, unstable. The challenge lies not in adding layers of correction, but in identifying the minimal sufficient structure.

Ultimately, the field will be judged not by the elegance of its algorithms, but by their parsimony. The goal is not to build a model of the world, but to uncover the model already present within the data. Every parameter added is an admission of failure – a tacit acknowledgement that the system remains, at its core, misunderstood. Clarity, after all, is a courtesy.

Original article: https://arxiv.org/pdf/2601.22328.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-02 18:26