Uncovering Hidden Physics with DISCOVER

Author: Denis Avetisyan

A new framework intelligently searches for mathematical equations governing scientific phenomena, leveraging the power of modern hardware.

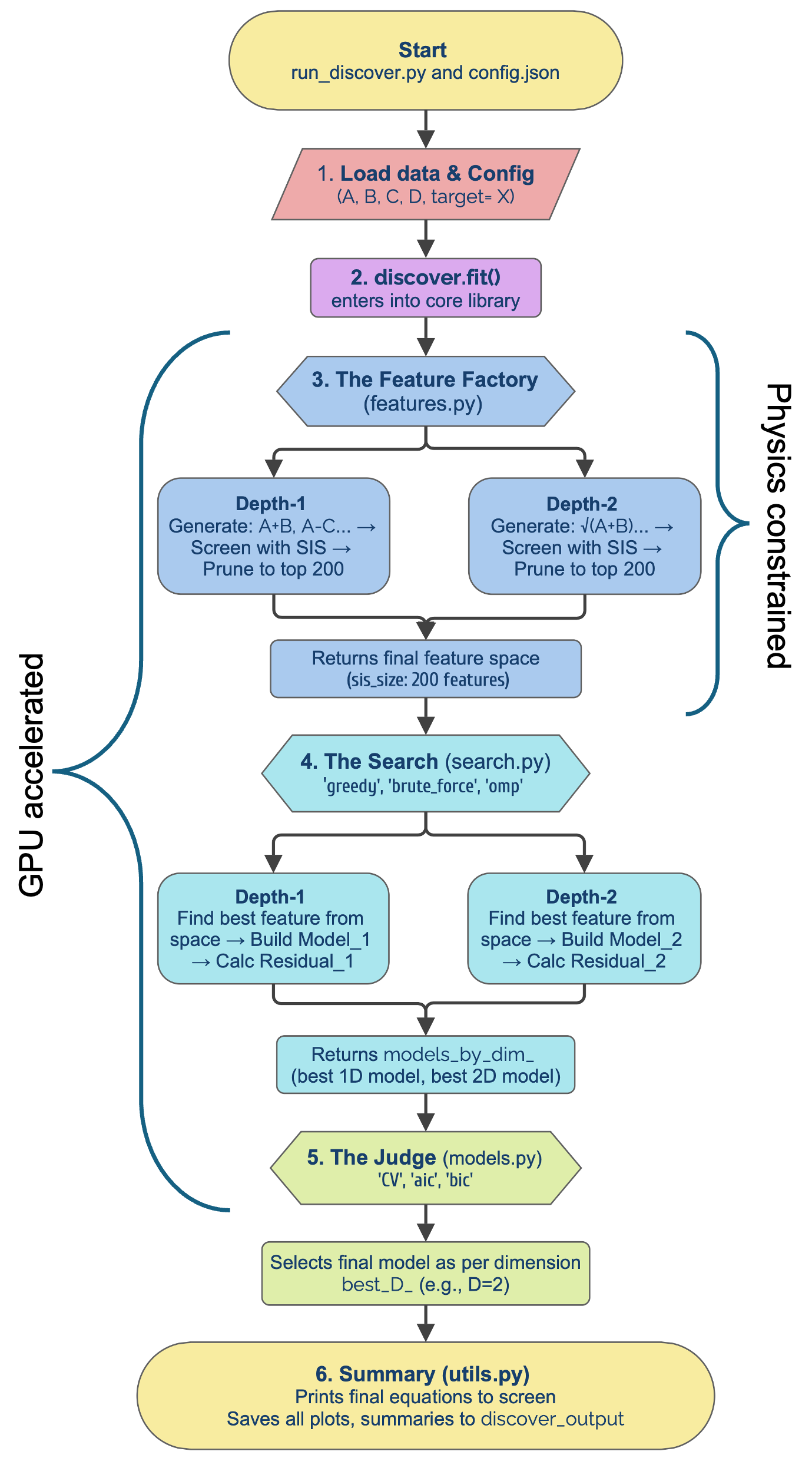
The DISCOVER workflow iteratively refines models through cycles of feature generation, physics-informed screening, and sparse selection, ultimately yielding a solution that balances descriptive power with computational efficiency.

DISCOVER is an open-source Python package for physics-informed symbolic regression that combines GPU acceleration, descriptor discovery, and dimensional consistency for scalable and interpretable model discovery.

Despite increasing data availability in scientific fields, extracting interpretable and physically consistent models remains a significant challenge. This paper introduces ‘DISCOVER: A Physics-Informed, GPU-Accelerated Symbolic Regression Framework’, an open-source Python package designed to address this limitation through a modular approach to symbolic regression. DISCOVER uniquely combines physics-informed constraints, optional GPU acceleration, and flexible feature space control to enable scalable and reproducible model discovery in materials science, chemistry, and physics. Will this emphasis on physically meaningful models unlock new avenues for scientific insight and accelerate the pace of discovery?

Unveiling Material Behavior: Beyond Empirical Trial and Error

Historically, the development of new materials has been a largely empirical undertaking, driven by researchers’ instincts and iterative experimentation. This approach, while often successful, is inherently inefficient; countless material combinations must be synthesized and tested, a process demanding significant resources and extended timelines. The reliance on trial-and-error not only increases the financial burden of materials science, but also limits the pace of innovation, as promising candidates can be overlooked amidst the vast compositional space and the subtle interplay of properties. Consequently, the advancement of materials capable of meeting increasingly complex technological demands is often hampered by the sheer logistical challenges of traditional discovery methods.

The design of advanced materials is frequently hampered by obscured relationships between a material’s intrinsic properties and its ultimate performance capabilities. It’s not simply that stronger or lighter materials are always superior; instead, nuanced interactions between characteristics like elasticity, thermal conductivity, and atomic structure dictate how a material behaves in a specific application. These connections are often non-linear and multi-faceted, meaning a small change in one property can trigger disproportionate effects on performance, while the interplay of multiple properties can create emergent behaviors difficult to predict through conventional analysis. Consequently, materials scientists often struggle to rationally design materials with targeted characteristics, relying instead on iterative experimentation and serendipitous discovery-a process that limits innovation and increases development costs.

The landscape of materials science is defined by combinatorial complexity; the number of possible material compositions and structural arrangements quickly escalates into astronomical figures, far exceeding the capacity for traditional, step-by-step experimentation. A truly exhaustive search for optimal materials – even within limited chemical spaces – is fundamentally impractical given current resources and timescales. This necessitates the development of intelligent approaches, such as high-throughput computation, data mining of existing materials databases, and machine learning algorithms capable of predicting material properties from composition. These techniques don’t aim to replace experimentation, but rather to intelligently narrow the search space, guiding researchers towards the most promising candidates and accelerating the pace of materials discovery by orders of magnitude. The challenge, therefore, isn’t simply generating data, but distilling meaningful insights from the overwhelming possibilities.

Advancing materials science demands analytical techniques that surpass the limitations of identifying mere correlations within datasets. While statistical relationships can suggest associations between material features and performance, they often fail to reveal the fundamental mechanisms driving these connections. Researchers are increasingly employing techniques – such as physics-informed machine learning and symbolic regression – to extract governing equations and causal relationships directly from experimental and simulation data. These methods aim to decipher the underlying physics and chemistry, allowing for predictive modeling that extends beyond the observed data and enables the rational design of materials with targeted properties. Ultimately, uncovering these mechanisms shifts the field from empirical observation toward a deeper, more principled understanding of material behavior, accelerating innovation and reducing reliance on costly trial-and-error approaches.

Decoding Material Laws: The Power of Symbolic Regression

Symbolic regression differs from traditional machine learning approaches by directly determining a mathematical equation, expressed in a human-readable form, that accurately models the relationship within a given dataset. Rather than learning a mapping from inputs to outputs – as in most supervised learning – symbolic regression algorithms search for a function [latex] f(x) = y [/latex] that best fits the data. This is achieved by exploring a space of possible mathematical operations – including addition, subtraction, multiplication, division, exponentiation, and trigonometric functions – and combining them with input variables to create candidate equations. The performance of each equation is evaluated using a fitness metric, typically based on the error between the predicted values and the observed data, and the best-performing equations are iteratively refined through techniques such as genetic programming to optimize their accuracy and complexity.

Traditional machine learning models, often referred to as “black boxes,” provide predictions without revealing the reasoning behind them. Symbolic regression, conversely, delivers results in the form of explicit mathematical equations. These equations, such as [latex]y = ax^2 + bx + c[/latex], directly express the relationships between input variables and the predicted output. This interpretability is crucial for scientific discovery and engineering applications, allowing users to not only predict outcomes but also understand how the inputs influence the output, validate the model against known principles, and potentially uncover previously unknown laws governing the data.

Symbolic regression employs evolutionary algorithms – specifically, techniques inspired by biological evolution – to navigate the extensive search space of potential mathematical expressions. These algorithms maintain a population of candidate equations, iteratively applying selection, crossover, and mutation operators. Equation fitness is evaluated based on its ability to accurately predict observed data, typically using a metric like mean squared error. Higher-performing equations are preferentially selected for reproduction, creating new equations through crossover (combining parts of existing equations) and mutation (introducing random changes). This process repeats over many generations, driving the population toward equations with increasing predictive power and complexity, ultimately identifying those that best model the underlying data relationships. The algorithm does not require prior knowledge of the equation’s form; it discovers the mathematical structure directly from the data.

Constraining symbolic regression with domain knowledge, specifically known physical principles, significantly improves the efficiency and relevance of the discovered models. This is achieved by incorporating terms, operators, and constants reflective of the underlying physics into the genetic programming process, thereby reducing the search space to only physically plausible equations. For example, when modeling projectile motion, incorporating terms for gravity [latex]g[/latex], initial velocity [latex]v_0[/latex], and time [latex]t[/latex] biases the search towards solutions containing these variables, rather than arbitrary mathematical forms. This approach not only accelerates convergence but also ensures that the resulting equation represents a physically meaningful relationship, enhancing interpretability and predictive accuracy within the defined physical system.

DISCOVER: An Optimized Framework for Scientific Insight

DISCOVER utilizes symbolic regression as its core methodology for identifying mathematical relationships within data. This process involves searching the space of possible equations to find the one that best fits the observed data, without predefining the functional form. The framework is implemented in Python to facilitate rapid prototyping and integration with existing scientific computing ecosystems. This implementation provides a structured workflow encompassing data preprocessing, model generation, equation simplification, and validation, streamlining the typically iterative process of symbolic regression. The resulting Python-based system allows researchers to efficiently explore potential models and derive interpretable equations directly from data, offering an alternative to traditional methods reliant on pre-specified model structures.

DISCOVER integrates physics-informed constraints through the use of the Pint library, a Python package for handling physical units and dimensional analysis. This integration enforces unit awareness during symbolic regression, ensuring that all intermediate and final expressions are dimensionally consistent. Specifically, Pint is used to define and propagate units associated with variables and constants, enabling the validation of candidate equations against expected unit profiles. This dimensional checking is performed during the symbolic regression process, eliminating physically implausible solutions early on and increasing the reliability of the discovered models. The system leverages Pint’s capabilities for unit arithmetic and conversion to maintain consistency throughout the derivation of equations.

DISCOVER significantly reduces computational time by utilizing GPU acceleration via both NVIDIA CUDA and Apple Metal Performance Shaders. This parallel processing capability is crucial when performing the intensive calculations inherent in symbolic regression and sparse model discovery. Specifically, the framework offloads computationally expensive operations – such as evaluating numerous candidate equations and performing optimization routines – to the GPU. This results in substantial speedups compared to CPU-based implementations, enabling researchers to explore larger datasets and more complex models within a feasible timeframe. The performance gains are particularly pronounced when dealing with high-dimensional data or when the search space of possible equations is extensive.

DISCOVER incorporates sparse model discovery techniques – Orthogonal Matching Pursuit, Mixed-Integer Quadratic Programming, and Simulated Annealing – to generate models with improved generalization and interpretability. The underlying optimization problem seeks a linear combination of input features exhibiting sparsity, effectively reducing model complexity and preventing overfitting. This is achieved by limiting the maximum dimensionality, D, of the descriptor space, as formally defined in equation (1). The resulting models, composed of fewer terms, are therefore less susceptible to noise and more readily interpretable than fully parameterized alternatives, contributing to increased robustness and predictive accuracy.

Towards Robust and Efficient Materials Modeling

The DISCOVER framework actively leverages AI Refactoring to ensure the resulting code base remains exceptionally clear and easily maintained. This process isn’t merely cosmetic; it involves automated analysis and restructuring of the code generated during materials discovery. By applying principles of software engineering, the system reduces complexity, eliminates redundant code, and improves overall architectural design. Consequently, researchers can more readily understand, modify, and extend the DISCOVER functionality, accelerating the pace of materials innovation and fostering collaborative development. This focus on code quality isn’t simply a matter of good practice; it directly impacts the reliability and scalability of the entire discovery pipeline.

Within the DISCOVER framework, L0 regularization functions as a powerful feature selection technique, dramatically streamlining the models generated. Unlike methods that merely shrink less important coefficients, L0 regularization forces many to become precisely zero, effectively eliminating irrelevant terms from the final equation. This approach doesn’t just simplify the model; it actively combats overfitting – a common issue where models perform well on training data but fail to generalize to new, unseen data. By focusing exclusively on the most significant descriptors – those with non-zero coefficients – the resulting models exhibit enhanced predictive power and improved robustness, requiring less computational resources and offering greater interpretability. The technique ensures that the model prioritizes the truly influential factors, creating a parsimonious representation of the underlying relationships within the data.

DISCOVER streamlines materials modeling by prioritizing the most impactful material properties, a process achieved through descriptor identification techniques such as Single Instance Spectral Subspace Optimization (SISSO). Rather than exhaustively analyzing all potential factors, SISSO effectively isolates key descriptors – those properties that exert the greatest influence on a material’s behavior. This focused approach dramatically reduces the computational burden of model development and enhances predictive accuracy. By concentrating modeling efforts on these critical descriptors, DISCOVER circumvents the complexities introduced by less relevant properties, ultimately accelerating the discovery of new materials with desired characteristics and fostering a more efficient research workflow.

The convergence of AI refactoring, L0 regularization, and sparse identification techniques within DISCOVER yields models distinguished by both accuracy and computational efficiency. By prioritizing the most impactful material properties and rigorously eliminating superfluous terms, the system constructs sparse models – those with minimal parameters – without sacrificing predictive power. This streamlined structure translates directly into faster computation times and reduced memory requirements, making these models particularly well-suited for deployment in resource-constrained environments or for large-scale simulations. The resulting models aren’t simply accurate; they represent a significant advancement in creating materials science tools that are both insightful and practically viable, offering a pathway toward accelerated discovery and optimized material design.

“`html

DISCOVER, as presented in this work, embodies a crucial intersection of computational power and fundamental principles. The framework’s emphasis on physics-informed constraints – ensuring dimensional consistency and leveraging known physical laws – resonates deeply with the notion that observation without interpretation remains incomplete. As Isaac Newton famously stated, “If I have seen further it is by standing on the shoulders of giants.” This framework doesn’t merely accelerate the process of model discovery, but actively builds upon established scientific understanding, ensuring that computational exploration is grounded in a robust theoretical foundation. The scaling capabilities offered by GPU acceleration are not simply about speed; they are about expanding the scope of inquiry, allowing researchers to test increasingly complex hypotheses while remaining tethered to the principles of physics and dimensional analysis, preventing acceleration without direction.

What Lies Ahead?

The automation of scientific discovery, as exemplified by frameworks like DISCOVER, presents a curious paradox. The pursuit of elegant equations, once a distinctly human endeavor, increasingly relies on algorithms to sift through data and propose relationships. Yet, the very act of defining ‘physics-informed’ constraints encodes specific ontological assumptions – a worldview regarding the fundamental nature of reality. The framework’s success hinges not only on computational efficiency, but on the careful consideration of which priors are baked into the search process. Transparency is minimal morality, not optional.

Scalability, even with GPU acceleration, addresses a symptom, not the disease. The exponential growth of possible equations remains a significant hurdle. Future work must address the limitations of descriptor discovery – how effectively can the system represent the complexity of physical systems without being overwhelmed by irrelevant features? A critical question arises: can algorithms truly generalize beyond the training data, or are they merely sophisticated pattern-matching machines?

The promise of automated scientific modeling carries an implicit responsibility. It is not enough to create algorithms that can discover equations; it is crucial to understand which equations are being discovered, and why. The field will be defined not solely by algorithmic innovation, but by the development of rigorous methods for validating and interpreting the models they produce. The world is created through algorithms, often unaware.

Original article: https://arxiv.org/pdf/2602.06986.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Unveiling Material Behavior: Beyond Empirical Trial and Error

Decoding Material Laws: The Power of Symbolic Regression

DISCOVER: An Optimized Framework for Scientific Insight

Towards Robust and Efficient Materials Modeling

What Lies Ahead?

See also: