Smarter Paths: Reinforcement Learning for Adaptive Random Walks

Author: Denis Avetisyan

This review explores how intelligent agents, leveraging reinforcement learning, navigate discrete spaces to optimize encounter probabilities and explore complex environments.

The analysis of random walker meetings on a discrete space reveals that encounter times-visualized through a factorized representation of meeting times across individual walker subspaces-exhibit a distinct pattern, with a central trough indicating zero encounters when both walkers originate from the same cell, demonstrating a relationship between starting position and the likelihood of interaction.

The study introduces configuration entropy as a novel metric for quantifying agent intelligence in the context of Markovian random walks and game-theoretic scenarios.

Understanding how simple agents learn to navigate and interact within complex environments remains a fundamental challenge in artificial intelligence. This is addressed in ‘Smart Walkers in Discrete Space’, where we investigate the emergent behaviors of trainable agents operating as random walkers and employing reinforcement learning to optimize encounter probabilities. We demonstrate that adaptive strategies measurably alter encounter statistics and, crucially, identify configuration entropy as a robust proxy for quantifying learned skill, even without direct access to reward signals or policy details. Does this entropy-based measure offer a generalizable framework for evaluating intelligence across diverse agent-based systems and learning paradigms?

Beyond Markovian Chains: The Limits of Traditional AI

Conventional planning methodologies frequently depend on the framework of fully observable Markov Chains, a system that assumes complete knowledge of the current state and predictable transitions. However, this reliance presents significant limitations when applied to the intricacies of real-world scenarios. Unlike idealized models, most environments are only partially observable, meaning an agent doesn’t have access to all relevant information; consider a robotic navigation task where sensor data is imperfect or a financial market influenced by countless unpredictable factors. Furthermore, Markov Chains assume the future depends solely on the present state, neglecting the influence of historical context or latent variables. This simplification fails to capture the nuances of dynamic systems where past events can profoundly affect future outcomes, hindering the development of truly robust and adaptable agents capable of navigating uncertainty and complexity.

The limitations of static, pre-programmed agents become strikingly apparent when confronted with the inherent unpredictability of real-world environments. Consequently, a significant drive in artificial intelligence research centers on developing agents capable of adaptive behavior – systems that can learn from experience and modify their actions to optimize performance amidst uncertainty. This pursuit extends beyond simply reacting to stimuli; it necessitates the ability to build internal models of the environment, predict future states, and formulate strategies that account for incomplete information and evolving conditions. Such agents require robust mechanisms for sensing, interpreting, and responding to change, moving beyond rigid, pre-defined rules towards flexible, learning-based approaches that enable them to thrive in dynamic and often chaotic settings.

Reinforcement Learning presents a compelling framework for developing agents capable of autonomous decision-making, yet its successful implementation hinges on two critical components: effective state representation and robust policy optimization. An agent must accurately perceive and encode its environment – a challenging task given the potential for vast and noisy sensory input – to construct a meaningful state representation. Simultaneously, the agent’s policy – the strategy governing its actions – must be continuously refined through trial and error, balancing exploration of new possibilities with exploitation of known rewards. Algorithms like Q-learning and policy gradients address this optimization challenge, but their performance is heavily influenced by the quality of the state representation; a poorly defined state can lead to suboptimal policies, even with sophisticated learning algorithms. Consequently, ongoing research focuses on developing techniques for automatically learning relevant state features and designing efficient policy optimization methods to navigate complex and uncertain environments.

Training performance, as measured by cumulative reward and both Shannon and configuration entropy, indicates that Alice learns most effectively with a sinusoidal reward function and consistently encodes information in her policy as training progresses.

Smart Walkers: Embracing Adaptability Through Learning

The Smart Walker represents an advancement over traditional Random Walkers by employing a learned policy to govern its movements. A Random Walker operates on purely stochastic principles, selecting actions without regard to past experience or potential future rewards. Conversely, the Smart Walker utilizes a policy – a mapping from states to actions – that is iteratively improved through interaction with its environment. This learned policy allows the agent to move beyond random exploration and exhibit goal-directed behavior, enabling it to navigate complex environments and optimize for specific objectives, unlike the purely probabilistic nature of the Random Walker.

The Q-Table is a central component of the Smart Walker, functioning as a lookup table that stores the expected cumulative reward for taking a specific action in a given state. Each entry, typically represented as Q(s, a), quantifies the anticipated long-term benefit of performing action ‘a’ while in state ‘s’. The table is initialized with arbitrary values, and subsequently updated through an iterative process. With each interaction with the environment, the Q-values are refined using the Bellman equation, incorporating the immediate reward received and the estimated future rewards achievable from the resulting state. This continuous updating allows the Smart Walker to learn an optimal policy by accurately representing the expected return for each state-action pair.

The Smart Walker employs Reinforcement Learning to optimize its movement policy through iterative improvement. This process involves the agent taking actions within its environment, receiving a reward signal based on those actions, and updating its internal policy to favor actions that yield higher cumulative rewards. The agent doesn’t receive explicit instructions; instead, it learns through trial and error, adjusting its behavior based on the observed consequences. This iterative refinement continues over numerous episodes, allowing the Smart Walker to progressively maximize its performance-measured by the total reward accumulated-within the defined environment. The learning rate and discount factor parameters control the speed and emphasis on future rewards, respectively, influencing the efficiency and stability of policy convergence.

Configuration entropy, calculated from observing Stockfish play against a random opponent over multiple games, monotonically decreases with skill level, suggesting its potential as a metric for agent ability, with a notable gap between levels 19 and 20 indicating a non-artifactual shift in playing style.

Modeling State Transitions: The Elegance of Markovian Dynamics

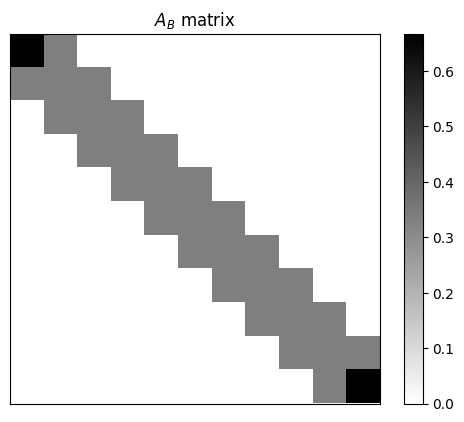
The operational behavior of a Smart Walker is fundamentally determined by its Transition Matrix, a mathematical representation of state transitions. This matrix, denoted as [latex]P[/latex], defines the conditional probability [latex]P_{ij}[/latex] of transitioning from state i to state j in a single time step. Each element within the matrix, ranging from 0 to 1, quantifies the likelihood of a specific transition; the sum of probabilities for all transitions from a given state must equal 1. Consequently, the Transition Matrix serves as a complete probabilistic model of the agent’s dynamics, enabling prediction of future states based on the current state and defining the possible movements and actions of the Smart Walker.

Calculating the Transition Matrix for a Smart Walker’s state transitions can be computationally expensive, particularly as the number of states increases; however, techniques such as utilizing the Kronecker Product offer significant reductions in complexity. The Kronecker Product allows decomposition of a larger state transition matrix into smaller, more manageable matrices, reducing the computational cost from [latex]O(n^4)[/latex] to [latex]O(n^2)[/latex] where ‘n’ represents the number of states. This is achieved by representing the overall transition as a tensor product of lower-dimensional matrices, enabling parallelization and more efficient computation, especially crucial for real-time applications and complex robotic behaviors.

The Markovian property, specifically the memoryless characteristic, simplifies the modeling of Smart Walker state transitions by asserting that the probability of transitioning to a future state depends solely on the current state, not on the sequence of past states. This allows for the application of analytical techniques, such as calculating long-term state distributions and predicting future behavior based on the current state and the defined transition probabilities within the [latex]Transition Matrix[/latex]. Predictive modeling leverages this property to estimate the likelihood of the agent being in a particular state after a given number of steps, enabling the assessment of potential trajectories and informing control strategies. Furthermore, the Markovian assumption facilitates the use of established mathematical frameworks for analyzing stochastic processes, providing tools for quantifying uncertainty and optimizing performance.

The transition matrices demonstrate that, absent interaction, the two agents perform independent random walks governed by reflecting boundary conditions.

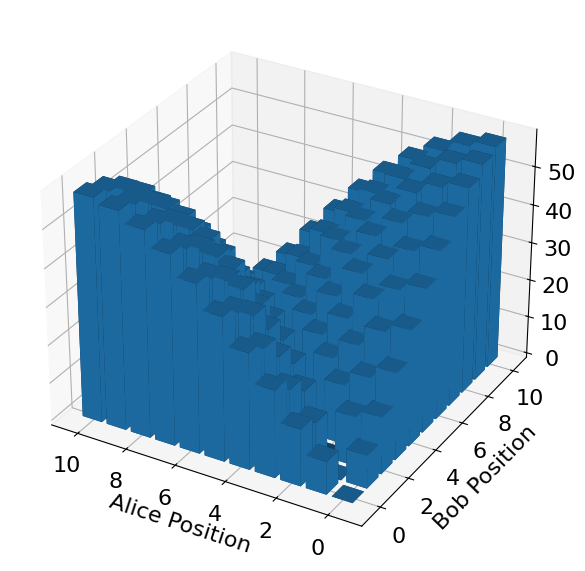
Predicting Encounters: Quantifying the Potential for Interaction

In multi-agent systems, predicting interactions is paramount, and the concept of ‘Encounter Probability’ provides a quantifiable measure of this potential. This metric doesn’t simply indicate if agents will meet, but rather the likelihood of such an event occurring within a defined timeframe and space. Calculated by analyzing agent trajectories and movement patterns, a higher Encounter Probability suggests a greater chance of interaction, which is crucial for coordinating behaviors, sharing information, or even avoiding collisions. This value isn’t static; it dynamically shifts based on agent positioning, velocities, and the surrounding environment. Consequently, understanding and predicting Encounter Probability is fundamental to designing effective algorithms for swarm robotics, network communication, and modeling complex systems where agent interactions drive overall behavior.

Understanding when agents will meet proves as vital as knowing if they will, and the concept of ‘Meeting Time’ directly addresses this need for precise coordination. This metric moves beyond simply calculating encounter probabilities by quantifying the expected duration before two agents converge, allowing for proactive strategy development. For instance, in robotic swarms, agents can utilize Meeting Time to synchronize tasks, ensuring resources arrive just as needed, or to avoid collisions by adjusting trajectories. Similarly, in network analysis, predicting the time until information reaches a critical node becomes possible, improving efficiency and resilience. The implications extend even to biological systems, offering insights into the timing of interactions between organisms – from predator-prey encounters to the formation of symbiotic relationships – making Meeting Time a powerful analytical tool across diverse scientific fields.

The analytical framework developed through the Smart Walker’s movement patterns extends far beyond robotic coordination. Calculating encounter probabilities and predicting meeting times provides a powerful tool applicable to diverse fields; in network analysis, these metrics can model information diffusion and identify critical nodes, while in robotics, they enable more efficient multi-robot task allocation and collision avoidance. Perhaps surprisingly, the same principles illuminate biological interactions – researchers can utilize these calculations to model predator-prey dynamics, analyze flocking behavior, or even predict the spread of disease within a population, demonstrating a fundamental connection between seemingly disparate systems and offering a unified approach to understanding complex interactions across scales.

The first encounter probability distributions, obtained through numerical simulations [latex](10,000 imes 10,000)[/latex] games post-learning, align with those predicted by the analytical solution [latex](3.6)[/latex].

Benchmarking and Validation: Beyond Simulation, Towards Robust Intelligence

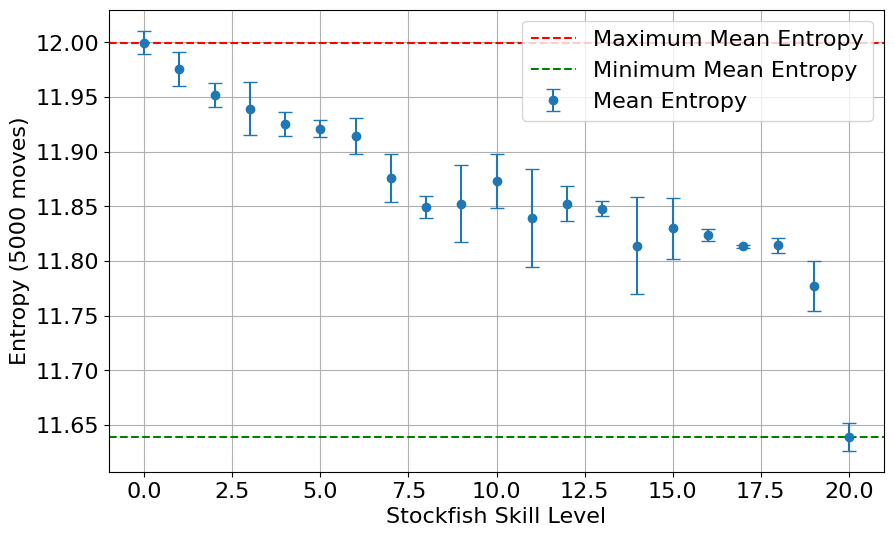
The Smart Walker framework’s efficacy is rigorously demonstrated through direct performance comparisons with leading chess engines, notably Stockfish. This validation process extends beyond simple simulations by benchmarking the framework against a well-established and highly optimized artificial intelligence. By assessing Smart Walker’s performance relative to Stockfish – a program renowned for its strategic depth and tactical precision – researchers establish a quantifiable measure of the framework’s capabilities in complex decision-making scenarios. This approach not only confirms the framework’s functionality but also provides a basis for identifying areas for improvement and refinement, ultimately driving the development of more robust and intelligent agents.

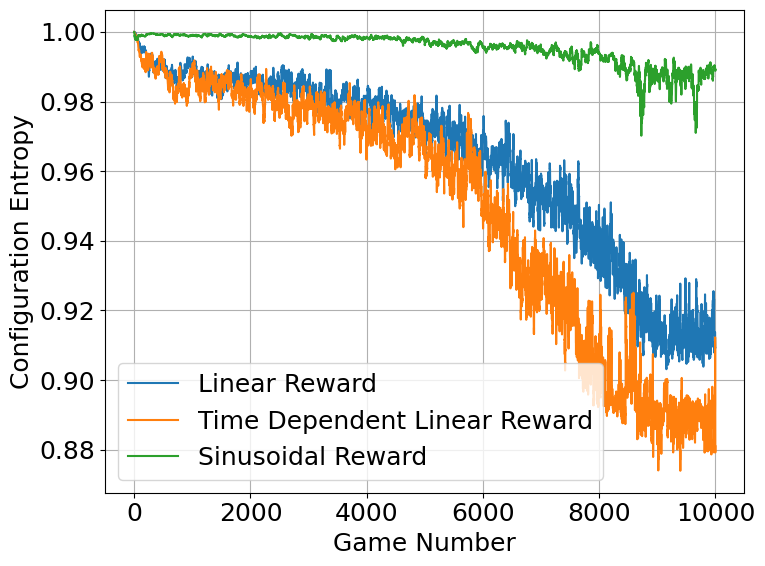
Configuration entropy provides a quantifiable measure of an agent’s policy complexity and its capacity to adapt to diverse situations. Essentially, it gauges the breadth of viable actions an agent considers at each decision point; a higher entropy suggests a more exploratory and versatile strategy, while a lower value indicates a more focused, deterministic approach. Importantly, studies reveal a strong correlation between configuration entropy and agent skill – as an agent becomes more proficient, its policy typically streamlines, reducing unnecessary complexity and converging towards optimal strategies. This decrease in entropy isn’t merely a byproduct of learning, but a fundamental indicator of improved competency, suggesting that truly skilled agents don’t simply consider more options, but rather, efficiently select the most promising ones from a refined and focused repertoire.

The study reveals a compelling relationship between an agent’s skill level and its decision-making complexity, quantified through a metric called ‘configuration entropy’. Researchers observed that as the chess engine Stockfish’s proficiency increased, its configuration entropy-a measure of the diversity of considered moves-systematically decreased, suggesting more efficient and focused strategic thinking. Notably, a distinct break in this trend occurred between skill levels 19 and 20, indicating a qualitative leap in competency rather than a simple incremental improvement. This discontinuity highlights a critical threshold where the agent transitions from exploring numerous possibilities to confidently selecting optimal moves, offering a valuable insight for designing artificial intelligence systems that can adapt and excel in increasingly complex environments and ultimately paving the way for more intelligent and efficient agents across diverse domains.

The study of these ‘smart’ random walkers, guided by reinforcement learning, reveals a fundamental truth about automated systems: intelligence isn’t merely about efficiency, but about the values embedded within the learning process. As Richard Feynman observed, “The first principle is that you must not fool yourself – and you are the easiest person to fool.” This resonates deeply with the paper’s exploration of encounter probabilities – a seemingly neutral metric that, when optimized without ethical consideration, could lead to skewed distributions and unintended consequences. The development of configuration entropy as a measure of agent intelligence highlights a critical need to evaluate not just how an algorithm learns, but what it learns, and the worldview encoded within its adaptive strategies. Scalability without such ethical grounding risks acceleration toward predictable, yet undesirable, outcomes.

Where Do These Walkers Lead?

The investigation of ‘smart’ random walkers, while framed as a problem in discrete space and reinforcement learning, gestures toward a far older question: how do simple agents, governed by local rules, generate complex, and potentially predictable, patterns of interaction? This work establishes configuration entropy as a metric for assessing adaptive behavior, but the very act of measuring intelligence invites scrutiny. Is maximizing encounter probability inherently ‘smart,’ or merely efficient within the parameters defined? The ethical implications, though subtle in this context of simulated walkers, are not absent. An engineer is responsible not only for system function but its consequences.

Future research should address the limitations of discrete space. Real-world encounters are rarely so neatly bounded. Moreover, the current framework prioritizes encounter probability over the quality of those encounters. A walker maximizing contacts with detrimental stimuli is, in a sense, highly effective, yet hardly intelligent. Extending this work to incorporate nuanced reward structures – acknowledging the valence of interactions – will be crucial.

Ultimately, this line of inquiry is not simply about optimizing random walks. It is about building models of agency, and agency implies responsibility. Ethics must scale with technology. The increasing sophistication of these ‘smart’ agents demands a parallel development in the frameworks used to evaluate, and constrain, their behavior.

Original article: https://arxiv.org/pdf/2601.22235.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/