Author: Denis Avetisyan
Researchers have developed a novel motion planning system that allows robots to navigate complex tasks by focusing on achievable contact points, rather than exhaustive state-space exploration.
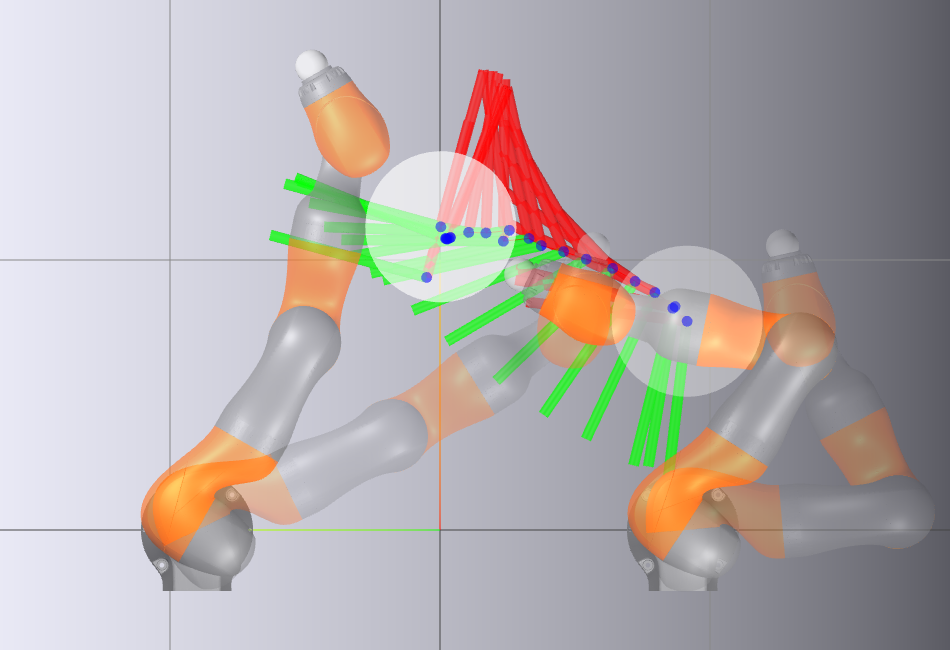
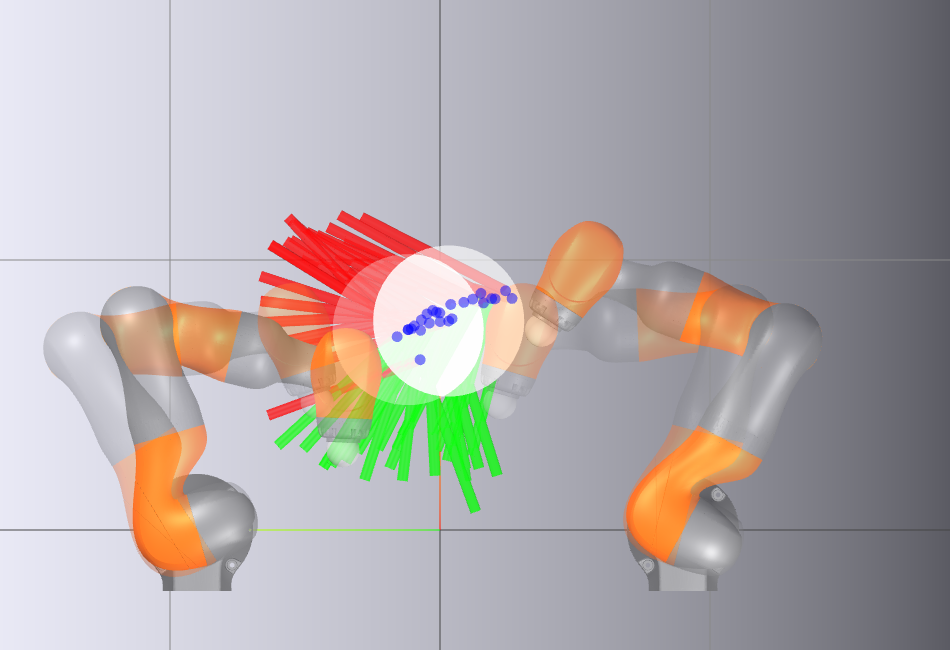
This work introduces a discrete planning space based on mutual reachable sets to improve efficiency and effectiveness in contact-rich SE(2) manipulation.
While robot manipulation often relies on precise end-effector control, human dexterity stems from leveraging the full surface of the hand for contact. This limitation motivates the work presented in ‘Approximately Optimal Global Planning for Contact-Rich SE(2) Manipulation on a Graph of Reachable Sets’, which introduces a novel planning paradigm utilizing a graph of mutual reachable sets to compute approximately optimal manipulator plans for contact-rich tasks. By effectively discretizing the planning space, this approach outperforms state-of-the-art methods, achieving substantial cost reductions and high success rates. Could this framework unlock truly adaptive and efficient robot manipulation capable of tackling complex, real-world scenarios?
Beyond Static Support: The Rise of Whole-Body Robotic Interaction
Historically, robotic manipulation has prioritized precise control of the end-effector – the hand or tool at the robot’s arm’s end – treating the rest of the body as a static support structure. This approach, while effective in highly structured environments like factory assembly lines, struggles when faced with the unpredictability of real-world scenarios. Complex environments introduce disturbances – uneven surfaces, unexpected obstacles, or the need to apply force at varying angles – that quickly overwhelm systems reliant on end-effector precision alone. The inherent limitation lies in the inability to dynamically adjust to these external forces and maintain stable interaction; a robot attempting to manipulate an object while bumping against obstacles, for example, requires more than just wrist adjustments – it demands coordinated movement and stabilization from the entire body to prevent losing control or damaging both itself and the surroundings.
Robotic manipulation extends far beyond the precise movements of a robotic hand; truly effective interaction with the physical world often demands the coordinated use of the entire robot body. Researchers are discovering that leveraging the robot’s base, torso, and even its gait, provides crucial stabilization during delicate tasks, allows for dynamic repositioning to overcome obstacles, and enables more nuanced interaction forces. This holistic approach moves beyond simply reaching for an object to actively shaping the robot’s posture to optimize force distribution, maintain balance, and adapt to unexpected disturbances. Consequently, robots can perform complex manipulations in cluttered or dynamic environments – tasks that would be impossible with end-effector control alone, such as assembling intricate parts, cooperating with humans, or navigating uneven terrain while maintaining a firm grasp.
As robotic tasks increase in complexity and move beyond highly structured environments, conventional planning and control methods prove inadequate for coordinating the nuanced movements required for full-body interaction. Successfully leveraging a robot’s entire body for manipulation necessitates algorithms capable of simultaneously optimizing numerous degrees of freedom, accounting for dynamic stability, and adapting to unforeseen external forces. Current strategies often rely on computationally expensive methods or simplified models, hindering real-time performance and robustness. Consequently, research is actively exploring novel approaches – including reinforcement learning, model predictive control, and whole-body optimization techniques – to develop more intelligent and adaptable systems that can seamlessly integrate whole-body coordination into complex manipulation tasks, ultimately enabling robots to perform intricate operations with greater efficiency and reliability.
Current robotic manipulation systems, largely designed around precise end-effector control, struggle with the unpredictable nature of real-world tasks and environments. These limitations stem from a reliance on pre-programmed trajectories and a difficulty adapting to unforeseen disturbances or variations in object properties. Consequently, a pressing need exists for manipulation frameworks exhibiting greater robustness – the ability to maintain performance despite external disruptions – and versatility, enabling robots to handle a wider range of objects and tasks without extensive re-programming. Such frameworks must move beyond simply positioning an end-effector and instead incorporate the robot’s full kinematic and dynamic capabilities, allowing for compliant movements, force control, and proactive adaptation to ensure successful and reliable interaction with complex environments.
Navigating Complexity: From Global to Local Planning Strategies
Full-body robot manipulation introduces a significant planning challenge due to the high dimensionality of the robot’s configuration space – encompassing not only joint angles but also end-effector pose and contact locations. This space, representing all possible robot configurations, scales exponentially with the number of degrees of freedom (DoF), typically exceeding 20 DoF for humanoid robots. Effective planning algorithms must efficiently search this space to identify collision-free trajectories that achieve desired tasks. These algorithms must account for kinematic and dynamic constraints, as well as potential contact forces, to generate feasible and stable motions. The computational complexity associated with searching such a high-dimensional space necessitates the use of efficient search strategies and approximations, such as randomized planning, hierarchical decomposition, or optimization-based methods, to enable real-time or near-real-time performance.
Global planning methods address the full-body robot configuration space by seeking comprehensive solutions, typically through either Mixed-Integer Programming (MIP) or Sampling-based Search. MIP formulates the planning problem as an optimization with discrete and continuous variables, enabling the identification of optimal trajectories but exhibiting exponential computational complexity with increasing dimensionality. Sampling-based Search, including algorithms like Probabilistic Roadmaps (PRM) and Rapidly-exploring Random Trees (RRT), addresses high dimensionality by randomly sampling the configuration space and constructing a graph or tree representing collision-free paths; while computationally more efficient than MIP, these methods do not guarantee optimality and solution quality depends heavily on sampling strategy and parameters. Both approaches require significant pre-computation and may struggle with real-time adaptation to dynamic environments due to their computational demands.
Trajectory Optimization (TO) is a local planning technique that generates dynamically feasible and often optimal robot motions over a finite time horizon. Unlike global planners, TO operates on a limited portion of the robot’s configuration space, enabling rapid computation and real-time responsiveness. The method formulates the planning problem as a constrained optimization, typically minimizing a cost function related to trajectory smoothness, energy expenditure, or task completion while satisfying kinematic and dynamic constraints. Common TO approaches include direct collocation and model predictive control (MPC), which iteratively solve for optimal control inputs given the current state and predicted future states. The short-term focus of TO necessitates frequent replanning to adapt to unforeseen circumstances or changes in the environment, but the computational efficiency allows for this to occur at high frequencies.
Effective adaptive manipulation necessitates the integration of both global and local planning strategies, fundamentally reliant on a comprehensive understanding of Contact Dynamics. Global planners establish feasible, long-horizon plans, accounting for kinematic and environmental constraints, but often lack the computational efficiency for real-time execution. Local planners, conversely, excel at rapidly generating trajectories for short-term movements, but require a global plan to provide context and avoid local optima. Contact Dynamics, encompassing the forces and constraints arising from interactions between the robot and its environment, is critical for both levels; accurate modeling allows global planners to generate collision-free paths and enables local planners to react effectively to unexpected disturbances or changes in contact configurations. This hierarchical approach-global planning for broad objectives and local planning for precise, reactive control-allows robots to perform complex manipulation tasks in dynamic and uncertain environments.
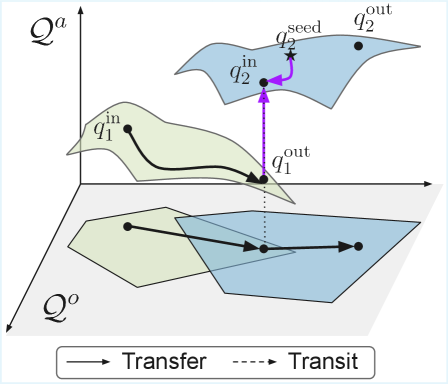
Mapping the Possible: Graph-Based Approaches to Workspace Exploration
The robot’s reachable workspace, essential for motion planning, is formally defined by its Configuration Space (C-Space). C-Space is an abstract space representing all possible configurations of the robot – that is, all possible values of its joint variables. Each point in C-Space corresponds to a unique pose of the robot in its operating environment. Defining C-Space allows for the simplification of the planning problem; instead of planning a path in the robot’s physical workspace, a path is planned through the higher-dimensional C-Space. Obstacles in the physical world map to obstacles within C-Space, representing configurations the robot cannot achieve due to collisions. The dimensionality of C-Space is determined by the robot’s degrees of freedom; a robot with n degrees of freedom will have an n-dimensional C-Space.
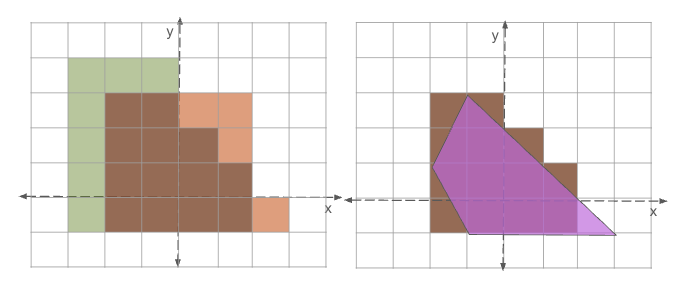
Representing a robot’s workspace as a graph of convex sets facilitates efficient motion planning by discretizing the configuration space into a network of simplified geometric shapes. Each node within the graph corresponds to a convex region in the robot’s configuration space, and edges define connectivity between these regions, indicating possible transitions between configurations. This approach reduces the computational complexity of collision detection and path searching; algorithms can operate on the simplified convex shapes rather than the original, potentially complex, geometries. The efficiency gains stem from the ability to quickly determine if a path exists between two configurations by traversing the graph and performing collision checks against the convex sets, which are computationally less expensive than checking against arbitrary polygons or surfaces. Furthermore, the graph structure allows for the application of established graph search algorithms, such as A* or Dijkstra’s, to find optimal or near-optimal paths.
Convex approximation techniques address the computational challenges posed by non-convex workspaces by replacing complex geometries with a collection of simpler, convex shapes. This simplification is achieved through various methods, including decomposition into convex hulls or the use of generalized convex primitives. While introducing a degree of error, this approach significantly reduces the complexity of collision detection and path planning algorithms. The accuracy of the approximation is directly related to the number and complexity of the convex shapes used; a higher number generally yields greater accuracy but increased computational cost. This trade-off is a key consideration in implementing these techniques, balancing the need for precise representation against real-time performance requirements.
Mutual Reachable Sets (MRS) refine workspace representation by focusing on the range of possible interactions between the robot and objects within its environment, defined in Object Space rather than joint configuration space. These sets identify configurations where both the robot and an object can simultaneously reach a specific location or pose, facilitating collision-free manipulation and grasp planning. The creation of MRS involves identifying pairs of robot and object configurations that allow interaction, and then representing the combined reachable space as a single set. This approach is particularly useful for tasks requiring coordinated manipulation, as it directly models the feasibility of interactions rather than relying on indirect assessments through configuration space alone; this can reduce computational complexity when compared to exhaustive sampling of the combined configuration space.
Optimizing for Performance: Tools and Frameworks for Efficient Manipulation
Trajectory optimization offers a powerful means of achieving precise robotic motion through the careful calculation of an optimal path. This approach utilizes sophisticated tools like Drake, a widely adopted toolbox for robotics research, alongside numerical solvers such as Snopt to refine a robot’s movements. Rather than relying on pre-programmed sequences, trajectory optimization formulates the control problem as a mathematical optimization, allowing the robot to dynamically adjust its trajectory to minimize error and maximize efficiency. By defining a cost function that encapsulates desired behaviors – such as minimizing energy expenditure or maximizing speed – and incorporating constraints related to the robot’s physical limitations, the solver identifies the sequence of joint angles and velocities that best satisfy these criteria, ultimately enabling remarkably accurate and controlled movements even in complex scenarios.
The pursuit of real-time robotic control often necessitates simplifying complex dynamic models. The quasi-dynamic assumption addresses this challenge by strategically neglecting certain inertial terms – specifically, those arising from the robot’s center of mass motion – under the rationale that their impact on joint-level torques is minimal in many manipulation scenarios. This simplification dramatically reduces computational demands, enabling faster calculations crucial for real-time feedback and control loops. By focusing on the dynamics directly influencing joint torques, the quasi-dynamic model achieves a balance between accuracy and speed, allowing robots to react quickly to changing environments and execute intricate movements without prohibitive processing delays. This approach is particularly valuable in scenarios demanding high responsiveness, such as contact-rich manipulation tasks where precise and timely control is paramount.
Sampling-based algorithms, like RRT-Connect, offer an efficient strategy for navigating the complex configuration space inherent in robotic manipulation. These algorithms don’t attempt to model the entirety of this space, which can be infinitely detailed, but instead intelligently sample potential robot configurations. RRT-Connect, in particular, builds a tree of reachable states by randomly connecting new samples to existing tree branches, rapidly exploring the configuration space and identifying collision-free paths. This approach proves particularly advantageous in high-dimensional spaces, where traditional optimization methods struggle with computational demands. By focusing on feasible connections rather than exhaustive search, RRT-Connect facilitates quick path planning, enabling robots to respond dynamically to changing environments and execute complex maneuvers with improved speed and efficiency.
The convergence of trajectory optimization, quasi-dynamic assumptions, and sampling-based algorithms unlocks significant advancements in robotic manipulation. Recent work demonstrates that a Graph of Reachable Sets (GRS) planning framework, integrating these techniques, substantially improves performance on complex tasks. Specifically, evaluations on a challenging contact-rich manipulation scenario reveal a 61% reduction in task cost and an impressive 91% planning success rate. This represents a considerable leap forward when contrasted with state-of-the-art sampling-based planners, suggesting that the combined approach not only accelerates execution but also enhances the reliability and efficiency of robotic systems tackling intricate manipulation challenges.
The Future of Robotic Manipulation: Learning and Adaptation
Behavior cloning represents a significant advancement in robotic manipulation by enabling robots to learn directly from human demonstrations. This approach bypasses the need for explicitly programming complex movements; instead, a robot observes an expert – a human performing the desired task – and learns to mimic those actions. Utilizing machine learning algorithms, the robot analyzes the human’s motions and corresponding sensor data, building a model that maps observations to appropriate control signals. Consequently, robots can acquire intricate skills, such as assembling delicate components or navigating cluttered environments, with considerably less engineering effort than traditional methods require. The efficacy of behavior cloning hinges on the quality and quantity of demonstration data, but it offers a particularly promising pathway toward creating robots capable of performing nuanced tasks in real-world settings.
Robotic manipulation is entering a new era where dexterity and adaptability are no longer limited by pre-programmed instructions. Current advancements focus on integrating learning-based approaches – where robots acquire skills through observation or trial-and-error – with established techniques in planning and optimization. This synergy allows robots to not only learn what to do, but also how to do it efficiently and reliably, even when faced with unpredictable circumstances. Rather than rigidly executing a predetermined sequence, these systems can dynamically adjust their actions, selecting optimal strategies based on real-time sensory input and environmental changes. This combination promises robots capable of handling a far wider range of tasks and operating effectively in complex, unstructured environments, moving beyond controlled factory settings and into the dynamic world humans inhabit.
The true potential of robotic manipulation lies in a combined approach, where learned behaviors and deliberate planning work in concert. Robots equipped with this synergy aren’t simply repeating demonstrated actions; they are adapting to novel situations within unpredictable, real-world environments. This means a robot could, for example, learn to grasp a variety of tools through observation, but then utilize path-planning algorithms to maneuver around obstacles and precisely position those tools for a specific task – even if that precise scenario wasn’t part of its original training. The result is a system capable of handling the inherent messiness and variability of unstructured spaces, allowing robots to move beyond controlled laboratory settings and perform increasingly complex tasks – from assembling intricate electronics in a cluttered workshop to assisting in disaster relief efforts amidst rubble and debris.
The long-term vision for robotic manipulation extends beyond mere automation; it centers on the development of robots capable of genuine interaction within human environments, functioning not as replacements, but as collaborators. These advanced systems aim to amplify human abilities – assisting with intricate tasks, extending reach into hazardous situations, and providing support for individuals with limited mobility. This isn’t simply about robots performing actions instead of people, but about enabling people to accomplish more, with greater ease and safety. Such capabilities promise significant improvements across diverse sectors, from healthcare and manufacturing to disaster relief and daily living, ultimately fostering a future where robotic assistance enhances quality of life for all.

The pursuit of approximately optimal global planning, as detailed in this work, echoes a fundamental tenet of systems architecture. The paper’s focus on defining a discrete decision space through mutual reachable sets demonstrates that effective control arises not merely from optimizing individual components, but from understanding the interconnectedness of the whole system. As David Hilbert stated, “In every well-defined mathematical problem there is a solution.” This resonates with the article’s approach; by meticulously mapping reachable sets and leveraging graph search, the research moves closer to solving the complex challenge of contact-rich manipulation, recognizing that even seemingly intractable problems yield to rigorous, systemic analysis. The architecture dictates the behavior, and the defined reachable sets become the very fabric of this behavior.
What Lies Ahead?
The construction of a discrete decision space predicated on mutual reachability offers a compelling, if subtle, shift in perspective. The efficacy demonstrated suggests that focusing on what is possible, rather than exhaustively detailing how it is achieved, may be a fruitful avenue for manipulation planning. However, the elegance of the proposed graph-based approach inherently highlights its limitations. The scalability of reachability analysis itself remains a critical bottleneck; the computational cost of defining these ‘reachable sets’ will undoubtedly increase as task complexity and environmental dimensionality grow. The current formulation implicitly assumes a relatively static environment; accommodating dynamic obstacles or uncertain contact dynamics will require careful consideration.
A natural extension of this work involves exploring alternative graph search heuristics, moving beyond optimality towards truly satisficing solutions-plans that are ‘good enough’ for practical application. Documentation captures structure, but behavior emerges through interaction. Future investigations should prioritize the integration of learning-based techniques to refine these reachable sets and adapt to unforeseen circumstances.
Ultimately, the true test of this approach lies not in its theoretical optimality, but in its robustness and adaptability when confronted with the messy realities of physical interaction. The question is not whether a plan is perfect, but whether it degrades gracefully in the face of imperfection-a principle often overlooked in the pursuit of algorithmic precision.
Original article: https://arxiv.org/pdf/2601.10827.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Clash Royale Best Boss Bandit Champion decks
- Vampire’s Fall 2 redeem codes and how to use them (June 2025)
- World Eternal Online promo codes and how to use them (September 2025)
- Best Arena 9 Decks in Clast Royale
- Country star who vanished from the spotlight 25 years ago resurfaces with viral Jessie James Decker duet
- ‘SNL’ host Finn Wolfhard has a ‘Stranger Things’ reunion and spoofs ‘Heated Rivalry’
- Solo Leveling Season 3 release date and details: “It may continue or it may not. Personally, I really hope that it does.”
- JJK’s Worst Character Already Created 2026’s Most Viral Anime Moment, & McDonald’s Is Cashing In
- M7 Pass Event Guide: All you need to know
- Kingdoms of Desire turns the Three Kingdoms era into an idle RPG power fantasy, now globally available
2026-01-20 00:38