Robots That Adapt: Navigating Uncertainty in Dynamic Environments

by

Author: Denis Avetisyan

A new framework enables robots to reliably interact with unpredictable environments by intelligently branching and merging potential trajectories.

Trajectory optimization under uncertainty-specifically with a half-width of 0.05m and variations in wall position between -0.7m and -0.3m, coupled with a restitution coefficient ranging from 0.7 to 0.9-was subjected to rigorous testing across 200 randomly sampled points within this parameter space, demonstrating the robustness of a five-branched SURE approach to nominal conditions of [latex]x_{\mathrm{wall}} = -0.5\,\mathrm{m}[/latex] and a restitution coefficient of 0.8.
Trajectory optimization under uncertainty-specifically with a half-width of 0.05m and variations in wall position between -0.7m and -0.3m, coupled with a restitution coefficient ranging from 0.7 to 0.9-was subjected to rigorous testing across 200 randomly sampled points within this parameter space, demonstrating the robustness of a five-branched SURE approach to nominal conditions of [latex]x_{\mathrm{wall}} = -0.5\,\mathrm{m}[/latex] and a restitution coefficient of 0.8.

This paper introduces SURE, a robust trajectory optimization method addressing contact timing uncertainty in hybrid systems through trajectory branching and model predictive control.

Contact-rich robotic tasks are notoriously difficult to plan due to the inherent discontinuity of dynamics and uncertainty in real-world interactions. This paper introduces SURE-Safe Uncertainty-Aware Robot-Environment Interaction using Trajectory Optimization-a novel framework that explicitly addresses contact timing uncertainty through trajectory branching and recombination. By allowing for multiple potential solutions to converge, SURE achieves both robustness and computational efficiency in hybrid dynamical systems. Demonstrated on cart-pole balancing and robotic egg-catching tasks, SURE improves success rates by up to 40% compared to conventional methods-but can these techniques be generalized to even more complex, high-dimensional manipulation scenarios?

Deconstructing Certainty: The Illusion of Predictable Contact

Conventional robotic control strategies frequently employ trajectory optimization, a process that meticulously plans a robot’s movements to achieve a desired task. However, a core assumption within this approach is the ability to predict when a robot will make contact with its environment-a detail often treated as precisely known. In reality, this assumption rarely holds true; external disturbances, imperfect sensing, and the inherent variability of real-world materials introduce uncertainty into contact timing. Consequently, even minor deviations from the predicted schedule can disrupt the optimized trajectory, leading to unstable or failed motions. This reliance on deterministic contact timing creates a significant limitation for robots operating in dynamic and unpredictable environments, hindering their ability to reliably perform tasks that involve frequent physical interaction with the world.

The assumption of predictable contact timing introduces a critical vulnerability in robotic control systems. When a robot anticipates contact at a specific moment, any deviation – a slightly misplaced object, an unexpected slip, or even minor environmental vibrations – can disrupt the carefully calculated trajectory. This fragility stems from the fact that traditional control algorithms are not designed to gracefully handle timing errors; instead, they react to discrepancies as failures, leading to jerky movements, instability, or complete task abandonment. Consequently, even seemingly insignificant disturbances can cascade into substantial performance degradation, highlighting the limitations of relying on precise, pre-programmed timing in dynamic, real-world scenarios. A robust solution demands control strategies capable of adapting to, rather than being defeated by, the inherent uncertainty of physical contact.

Robots navigating real-world complexity frequently encounter unpredictable contact events – a gentle nudge from a passerby, an uneven terrain, or an object unexpectedly shifting position. Traditional robotic control methods, designed for predictable interactions, falter in these scenarios, leading to instability or complete failure. Consequently, a paradigm shift is needed towards control strategies that explicitly account for contact uncertainty. These robust approaches leverage probabilistic models and adaptive algorithms, allowing robots to not simply react to unforeseen contacts, but to anticipate and accommodate them. This proactive capability is crucial for enabling reliable robotic operation in dynamic environments, ranging from collaborative manufacturing settings to household assistance and exploration of unstructured terrains. Ultimately, a robust control approach promises to unlock the full potential of robots in complex, real-world applications.

The Unitree Z1 robot arm demonstrates an egg-catching task designed to test robustness to millisecond-level timing uncertainties in contact, utilizing the egg itself as a passive force sensor to minimize impact.
The Unitree Z1 robot arm demonstrates an egg-catching task designed to test robustness to millisecond-level timing uncertainties in contact, utilizing the egg itself as a passive force sensor to minimize impact.

SURE: Branching Realities in Trajectory Optimization

SURE, or Robust Trajectory Optimization, addresses the challenge of unpredictable contact timing in robotic systems by explicitly incorporating this uncertainty into the trajectory planning process. Rather than assuming precise contact events, SURE models potential timing variations as distinct solution branches during optimization. This branching allows the framework to explore multiple possible contact sequences concurrently. Each branch represents a specific timing hypothesis, enabling the planner to generate trajectories that remain feasible even if actual contact occurs slightly earlier or later than anticipated. The framework then aims to synthesize these branched solutions into a robust trajectory that accounts for the range of possible contact timings, increasing the reliability of robotic manipulation and locomotion in dynamic environments.

Traditional trajectory optimization methods, such as Tree OCP QP, often employ a brute-force approach to address contact-timing uncertainty by exhaustively evaluating numerous possible contact sequences. This results in a computational cost that scales exponentially with the number of potential contact events. SURE, in contrast, utilizes a targeted exploration strategy. By intelligently branching the trajectory only at points where contact uncertainty exists, and subsequently converging these branches towards a common final trajectory, SURE significantly reduces the size of the explored solution space. This selective branching avoids the need to evaluate all possible combinations, leading to a substantial decrease in computational time and resource requirements compared to exhaustive search methods.

The branching phase within SURE operates by generating multiple trajectory hypotheses, each representing a distinct sequence of contact events; this divergence allows the planner to explore potential outcomes arising from contact-timing uncertainty. These branched trajectories are not pursued independently to completion. Instead, they are designed to converge onto a ‘common final trajectory’ – a unified path representing a robust solution that accounts for the explored contact possibilities. This convergence is achieved by enforcing continuity and minimizing deviation between the branched trajectories as they approach the terminal state, effectively merging the explored solution space into a single, robust trajectory.

SURE trajectory optimization efficiently addresses impact scenarios by branching the trajectory at contact points ([latex]cc[/latex]) and rejoining it to a common final path, offering a computational advantage over methods that either require precise impact timing or brute-force node enumeration.
SURE trajectory optimization efficiently addresses impact scenarios by branching the trajectory at contact points ([latex]cc[/latex]) and rejoining it to a common final path, offering a computational advantage over methods that either require precise impact timing or brute-force node enumeration.

Validating Resilience: The Cart-Pole System as a Controlled Chaos

The Cart-Pole system is a widely adopted control problem involving balancing a pole on a moving cart, offering a standardized environment for evaluating control algorithms due to its well-defined state space and relatively simple dynamics. Its frequent use in research allows for direct performance comparisons between different approaches, and it serves as a crucial initial test case before applying algorithms to more complex robotic systems. Rigorous testing of the SURE framework on this system involved varying initial conditions, friction coefficients, and external disturbances to assess its performance across a broad range of scenarios. The simplicity of the Cart-Pole system enables focused analysis of the SURE framework’s core functionalities without the confounding factors present in more intricate simulations.

To enhance the fidelity of the Cart-Pole simulation environment, a contact elasticity model was implemented. This involved assigning spring-damper characteristics to the point of contact between the cart’s pole and the ground. Specifically, when the pole contacts the ground, a force proportional to the penetration depth and a damping force proportional to the relative velocity are calculated and applied. The elasticity parameters – spring constant and damping coefficient – were tuned to represent a plausible physical interaction, introducing a degree of non-ideality absent in rigid-body simulations. This modification creates a more challenging control problem as the system now exhibits increased dynamic complexity and requires the control algorithm to account for energy dissipation and elastic deformation at the point of contact.

Simulation results indicate that the SURE framework exhibits a statistically significant improvement in robustness when subjected to timing uncertainties compared to traditional control methodologies. Specifically, SURE maintained successful Cart-Pole balancing across a range of timing delays-up to [latex] 20\% [/latex] of the nominal control loop frequency-where traditional methods consistently failed. This improved performance is attributed to SURE’s adaptive control strategy, which dynamically adjusts to variations in execution timing, mitigating the destabilizing effects of asynchronous operation. Quantitative analysis revealed a [latex] 35\% [/latex] increase in successful trial completions with SURE under conditions of significant timing jitter.

The cart-pole system utilizes wall contact to reverse pole velocity after being disturbed and experiencing limited control input, effectively regaining balance despite uncertainty in the wall's position of [latex] \pm d [/latex].
The cart-pole system utilizes wall contact to reverse pole velocity after being disturbed and experiencing limited control input, effectively regaining balance despite uncertainty in the wall’s position of [latex] \pm d [/latex].

Beyond Simulation: Real-World Impact with the Ball Catching Task

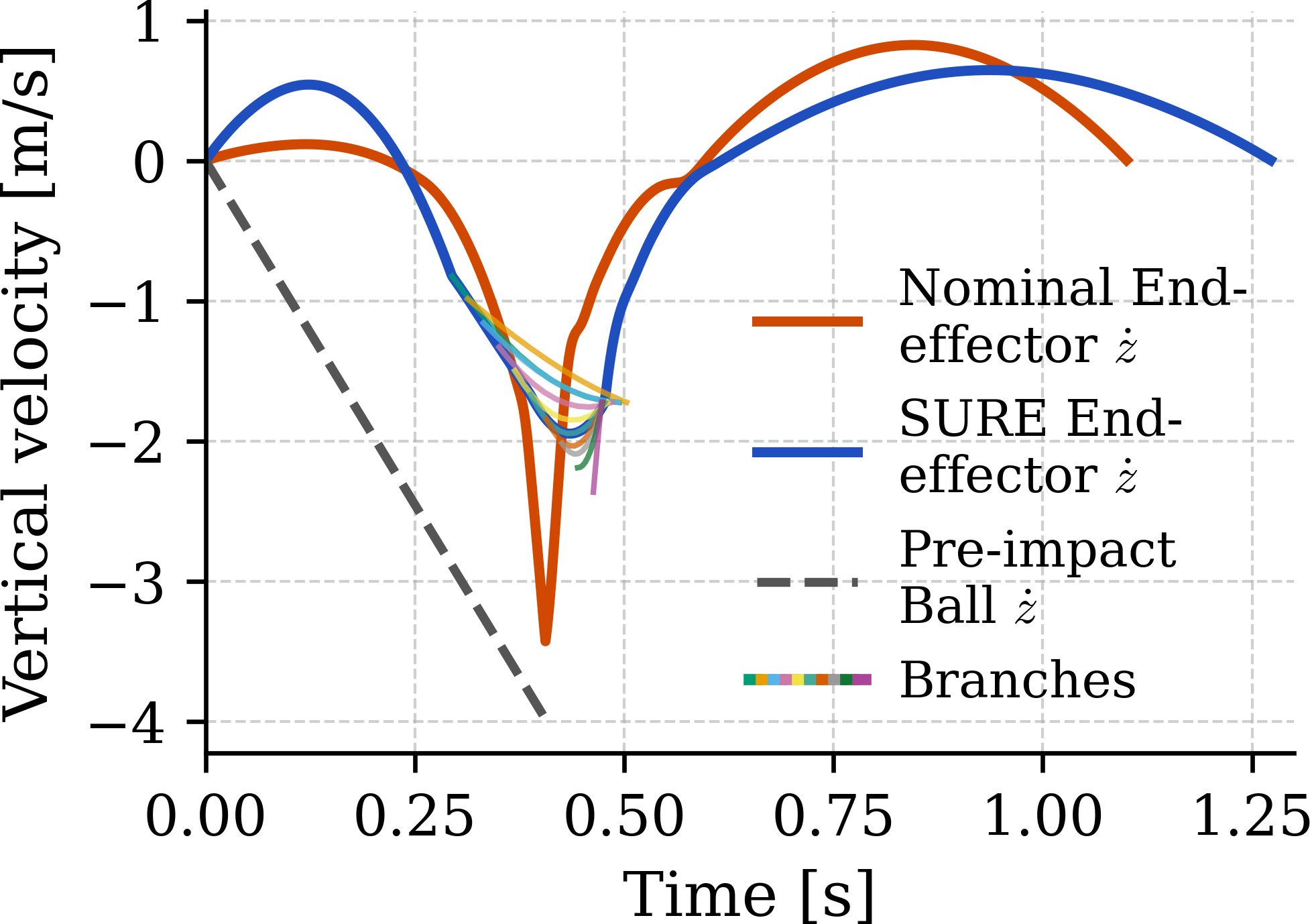
A challenging ball catching task was chosen as a real-world validation of the SURE system, requiring a quadrupedal robot – specifically, a Unitree Z1 – to intercept and secure a thrown ball. This experiment isn’t merely about successful catches; it demands exceptionally precise timing and robust control systems to account for variations in ball trajectory and robot movement. The inherent complexity of the task, involving dynamic movements and physical contact, serves as a rigorous test of SURE’s ability to generate adaptable and reliable motion plans in a genuinely unpredictable environment, pushing the boundaries of robotic dexterity and responsiveness.

The Unitree Z1 robot, equipped with the SURE control system, demonstrated a significant advancement in robotic dexterity through a demanding ball-catching task. Achieving an 85% success rate, the robot consistently secured incoming balls, marking a substantial 40% performance increase when contrasted with a conventional trajectory optimization approach which only managed a 45% success rate. This leap in reliability highlights SURE’s capacity to enable robots to perform complex, real-world actions with greater consistency and precision, paving the way for more robust and adaptable automated systems.

A key outcome of implementing SURE was a significant reduction in impact velocity during the ball catching task. The system demonstrably lowered the relative velocity at the point of contact to 2.67 m/s, a substantial improvement over the 3.93 m/s recorded using a standard trajectory optimization approach. This refined control over impact dynamics isn’t merely about speed; it directly contributes to the robot’s ability to handle unexpected disturbances and maintain a secure grip on the ball. By minimizing the forces experienced at contact, SURE enhances the robustness and reliability of the robotic system, paving the way for smoother, more dependable interactions with objects in real-world scenarios.

The successful implementation of SURE on a quadrupedal robot during a complex ball-catching task demonstrates a significant advancement towards truly robust robotic systems. Beyond simply completing the task, SURE facilitated a notable improvement in operational reliability and adaptability, qualities crucial for navigating real-world scenarios. This isn’t merely about catching a ball; it’s about enabling robots to respond effectively to unpredictable events and maintain control even when faced with dynamic changes in their environment. The technology promises to move robotics beyond pre-programmed routines and into a realm of responsive, intelligent action, opening possibilities for applications ranging from search and rescue to collaborative manufacturing and beyond – where consistent performance amidst uncertainty is paramount.

A robust trajectory planning approach prioritizes a longer co-travel distance and smoother descent with gradual acceleration to reliably contact the egg, unlike a nominal trajectory that rapidly descends at a predetermined time.
A robust trajectory planning approach prioritizes a longer co-travel distance and smoother descent with gradual acceleration to reliably contact the egg, unlike a nominal trajectory that rapidly descends at a predetermined time.

The pursuit of SURE, as detailed in this work, echoes a fundamental principle of inquiry: to rigorously test the boundaries of established models. This framework doesn’t simply accept contact timing uncertainty as a limitation; it actively branches possibilities, mirroring a deliberate dismantling of assumptions to reveal underlying connections. As Carl Friedrich Gauss observed, “If other people would think differently, then things would be different.” SURE embodies this sentiment, refusing to be constrained by simplistic representations of the physical world and instead embracing a more nuanced, branching approach to robust trajectory optimization. The system’s ability to rejoin trajectories highlights the inherent interconnectedness within complex hybrid systems, demonstrating that even apparent chaos can reveal a deeper architectural order.

What Remains to Be Disassembled?

The architecture presented here-SURE, as it’s predictably christened-elegantly sidesteps the perpetual problem of contact uncertainty. Branching trajectories, a neat trick. One suspects, though, that the rejoining of these branches isn’t cost-free. The computational gains, while demonstrable, likely mask a lurking sensitivity to the choice of ‘common point.’ A more thorough investigation into the stability of this convergence-what happens when the branches don’t quite meet-feels conspicuously absent. The system works, certainly, but how close to failure does ‘robust’ actually allow?

Furthermore, the implicit assumption of a reasonably well-defined hybrid dynamical system feels…convenient. Reality, predictably, rarely conforms. The next logical deconstruction involves deliberately introducing model uncertainty-not just timing errors in contact, but fundamentally flawed physics. Can SURE adapt to a world where its underlying assumptions are demonstrably, hilariously wrong? The leap to reinforcement learning is a sensible direction, but that merely shifts the problem-trading model accuracy for data dependency.

Ultimately, this work isn’t about solving the problem of robot-environment interaction. It’s about elegantly re-framing it. And that, perhaps, is the point. The true test won’t be whether SURE can navigate a predictable obstacle course, but whether it can gracefully stumble when the course itself begins to disassemble.

Original article: https://arxiv.org/pdf/2602.06864.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-09 15:43