Guiding the Swarm: AI-Powered Control of Large Agent Populations

by

Author: Denis Avetisyan

A new reinforcement learning approach enables sparse control of vast multi-agent systems, demonstrated through effective ‘shepherding’ of large groups.

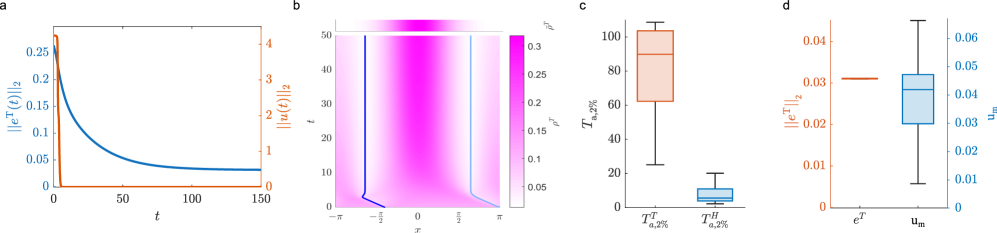
A learned policy, guided by a carefully constructed reward function and compensation law, demonstrates an emergent capacity to shepherd a target population, achieving convergence as measured by a $2$-norm of the target distribution error and control effort-a dynamic illustrated by the evolution of target density and herder positions over time-and exhibiting consistent settling times and steady-state errors across multiple experiments with randomized initial conditions.
A learned policy, guided by a carefully constructed reward function and compensation law, demonstrates an emergent capacity to shepherd a target population, achieving convergence as measured by a $2$-norm of the target distribution error and control effort-a dynamic illustrated by the evolution of target density and herder positions over time-and exhibiting consistent settling times and steady-state errors across multiple experiments with randomized initial conditions.

This work presents a scalable control strategy for multi-agent systems using sparse control and reinforcement learning to achieve optimal herding behavior even with limited control resources.

Controlling large populations of agents often presents a scalability challenge, demanding efficient strategies for collective behavior shaping. This is addressed in ‘Sparse shepherding control of large-scale multi-agent systems via Reinforcement Learning’, which proposes a reinforcement learning framework for indirectly guiding numerous agents using only a limited number of actively controlled ‘shepherds’. By coupling ordinary differential equations for controlled agents with a partial differential equation describing population density, the method achieves effective density control with sparse actuation and demonstrates robustness to disturbances. Could this learning-based approach offer a viable alternative to computationally intensive online optimization for large-scale multi-agent coordination?

The Inevitable Limits of Direct Command

The orchestration of expansive systems – be they robotic swarms, biological networks, or social collectives – frequently encounters a core limitation: the scarcity of control resources relative to the population size. This presents a fundamental challenge across diverse fields, from engineering and computer science to ecology and epidemiology. Effectively managing a large number of interacting entities demands a strategy that circumvents the need for direct, individualized command of each component. Traditional centralized control methods quickly become impractical due to communication bottlenecks, computational demands, and the sheer logistical complexity of coordinating vast numbers of agents. Consequently, researchers are increasingly focused on decentralized approaches that emphasize collective behavior and minimize the reliance on intensive, resource-hungry control signals, seeking scalable solutions for systems where complete, granular control is simply unattainable.

Conventional control strategies, while effective for smaller systems, frequently encounter limitations when applied to large-scale populations. These methods typically demand each agent receive and process individualized commands, creating a computational bottleneck as the number of agents increases. Furthermore, maintaining coordination often necessitates extensive communication networks, placing a significant strain on bandwidth and energy resources. The computational cost scales rapidly – often exponentially – with population size, while communication demands grow proportionally, rendering these approaches impractical for scenarios involving thousands or even millions of interacting entities. This inherent lack of scalability highlights the need for alternative control mechanisms that minimize both computational load and communication overhead, paving the way for more efficient and robust systems.

Shepherding control represents a paradigm shift in managing complex systems, moving away from direct, centralized regulation towards indirect guidance through carefully orchestrated interactions. Instead of issuing commands to each individual agent, this approach focuses on influencing the environment or a select few ‘shepherds’ within the population, allowing collective behavior to emerge through local interactions. This is particularly advantageous when dealing with large-scale systems where direct control is computationally expensive or physically impossible; the principle relies on the idea that a small number of well-placed influences can propagate throughout a network, steering the entire population towards a desired outcome. The efficiency of shepherding control stems from its ability to bypass the communication bottlenecks inherent in traditional methods, offering a scalable solution for coordinating complex behaviors in diverse fields like robotics, traffic flow, and even social networks.

This control architecture computes actions based on desired and sensed herder positions to influence the target distribution via a velocity field.
This control architecture computes actions based on desired and sensed herder positions to influence the target distribution via a velocity field.

Modeling the Flow: A Necessary Simplification

Modeling herder movement necessitates a foundational approach frequently utilizing kinematic assumptions to manage computational complexity. These assumptions typically involve treating herders as point masses subject to forces derived from desired velocities, cohesion with the herd, and avoidance of obstacles or targets. Rather than simulating detailed internal dynamics or cognitive processes, these models often employ simplified equations of motion, such as $v_i(t+Δt) = v_i(t) + a_i(t)Δt$, where $v_i$ is the velocity of herder and $a_i$ represents the net acceleration calculated from the aforementioned forces. This simplification allows for efficient simulation of large-scale herding behavior, although it inherently limits the model’s ability to capture nuanced individual actions or responses.

Mean-field theory provides a computationally efficient method for modeling the collective behavior of target agents by shifting the focus from tracking individual trajectories to analyzing population densities. This approach assumes that each target agent experiences an average interaction with the entire population, rather than specific interactions with individuals. Mathematically, this is often represented by describing the density of targets, denoted as $\rho(x, t)$, as a function of position $x$ and time $t$. The evolution of this density is then governed by equations that consider the aggregate effects of the population, simplifying the model while still capturing emergent behaviors like flocking or avoidance. This simplification is particularly useful when dealing with large numbers of agents where tracking individual movements would be computationally prohibitive.

The simulation of herder-target dynamics relies on mathematical formalisms to represent agent behavior and interactions. Ordinary differential equations (ODEs) are frequently used to model the continuous change of variables over time for individual agents or aggregated groups, particularly when dealing with deterministic systems. However, many realistic scenarios require the use of partial differential equations (PDEs) to account for spatial distributions and densities of agents. These PDEs often involve diffusion terms to represent random movement and interaction terms that define how agents influence each other, allowing for the simulation of emergent behaviors within the population. For example, a reaction-diffusion equation could model the spread of a herding response based on local density gradients, represented as $ \frac{\partial u}{\partial t} = D \nabla^2 u + f(u) $, where $u$ is the density of herders, $D$ is the diffusion coefficient, and $f(u)$ represents the herding interaction function.

This robustness analysis demonstrates the proposed control strategy effectively maintains target density distribution despite constant disturbances and measurement noise, as shown by consistent performance across varying disturbance levels and noise amplitudes.
This robustness analysis demonstrates the proposed control strategy effectively maintains target density distribution despite constant disturbances and measurement noise, as shown by consistent performance across varying disturbance levels and noise amplitudes.

Learning to Guide: A Reinforcement of Predictable Outcomes

Proximal Policy Optimization (PPO) is a reinforcement learning algorithm utilized to develop control policies for coordinating multiple agents – in this case, to optimize herding behaviors. PPO functions by iteratively refining a policy network through gradient ascent, while employing a clipped surrogate objective function to prevent overly large policy updates that could destabilize learning. This approach allows the controller to learn effective strategies for guiding agents towards a desired configuration, such as maintaining a specific density or reaching a target location, through trial and error within a simulated environment. The algorithm’s on-policy nature requires collecting new samples with the current policy at each iteration, ensuring stable and consistent improvements in the herding strategy.

The reinforcement learning process relies on a reward function to quantify the effectiveness of herding strategies, directly influencing the learned control policy. This function is parameterized by the target density, $ \rho_t $, representing the desired spatial distribution of the herded entities. A higher reward is assigned when the current density closely matches $ \rho_t $, encouraging the controller to adjust its actions to minimize the difference between the achieved and target distributions. Specifically, the reward is often formulated as a negative distance metric – such as mean squared error or Kullback-Leibler divergence – between the current density and $ \rho_t $, ensuring that the learning algorithm iteratively refines the control policy to achieve the desired herding configuration.

Numerical simulations provide a critical bridge between theoretical control policies and real-world application. Evaluating controller performance through simulation allows for the assessment of robustness across a variety of initial conditions and environmental disturbances without the risks or costs associated with physical experimentation. These simulations utilize computational models to replicate the dynamics of the herding environment, enabling iterative refinement of the control policy based on quantifiable metrics such as target density maintenance and energy expenditure. By systematically varying simulation parameters and observing the resulting behavior, developers can identify and address potential weaknesses in the control logic, ultimately leading to a more reliable and effective herding strategy before deployment in a physical system.

The PPO agent's episodic reward consistently increased during training, as indicated by the smoothed moving average.
The PPO agent’s episodic reward consistently increased during training, as indicated by the smoothed moving average.

The Inevitable Imperfections: A System’s Resilience

Maintaining effective control of multi-agent systems necessitates a focus on disturbance robustness, as real-world deployments are invariably subject to unpredictable external factors. These disturbances – encompassing variations in agent dynamics, environmental influences, or even communication disruptions – can severely degrade performance if not proactively addressed. Research demonstrates that systems lacking robust control strategies exhibit diminished accuracy and stability when confronted with such perturbations. Consequently, the development of control algorithms capable of mitigating the impact of disturbances is paramount; this often involves incorporating techniques like feedback control, adaptive strategies, or robust optimization to ensure consistent and reliable operation, even under adverse conditions. A system’s ability to gracefully handle unexpected influences directly translates to its practicality and dependability in dynamic, uncontrolled environments.

Practical application of multi-agent herding systems invariably encounters imperfections in sensory data, demanding that models account for measurement noise in the estimated positions of the herded agents. Without incorporating these realistic limitations, control algorithms can exhibit erratic behavior or fail to converge, as even minor inaccuracies in perceived agent locations propagate through the control loop and destabilize the overall system. Researchers are increasingly focused on employing techniques like Kalman filtering or robust estimation to mitigate the effects of this noise, effectively distinguishing between genuine agent movements and spurious readings. This allows for more reliable control signals, enabling the system to maintain formation and achieve desired aggregation densities even in the presence of imperfect information, ultimately bridging the gap between theoretical models and real-world deployments.

Effective flocking and collective behavior often require precise control over inter-agent interactions; therefore, compensating for variations in interaction strength is paramount for achieving desired group configurations. Research demonstrates that simply applying a control signal without accounting for these strengths can lead to uneven distributions and instability, as stronger interactions dominate the dynamics. By incorporating a compensation mechanism – often involving adjustments to control gains based on individual interaction parameters – the system can actively counteract these imbalances. This allows for the consistent realization of target densities, even when agents exhibit differing levels of responsiveness or are subject to heterogeneous environmental influences. Such compensation refines the control loop, promoting cohesive behavior and enabling the flock to maintain a stable, predetermined structure despite internal and external disturbances, ultimately enhancing the robustness and scalability of multi-agent systems.

Activating the compensation law at t ≥ 75 significantly reduces the L2 norm of the error state, demonstrating its effectiveness in mitigating system disturbances, as shown by the comparison to uncompensated error (a) and the corresponding time evolution of the interaction strength gain (b).
Activating the compensation law at t ≥ 75 significantly reduces the L2 norm of the error state, demonstrating its effectiveness in mitigating system disturbances, as shown by the comparison to uncompensated error (a) and the corresponding time evolution of the interaction strength gain (b).

The pursuit of scalable control, as demonstrated by this work on sparse shepherding, echoes a familiar refrain. One attempts to impose order upon complexity, believing a carefully designed architecture will yield predictable results. However, this paper subtly reveals the inherent limitations of such endeavors. It acknowledges that complete control is an illusion; instead, effective guidance-achieving desired outcomes with minimal intervention-is the pragmatic goal. As Bertrand Russell observed, “The good life is one inspired by love and guided by knowledge.” This sentiment applies here; the ‘knowledge’ being the acceptance of inherent systemic chaos, and ‘love’ manifesting as a gentle, sparse influence, allowing the system to evolve within acceptable bounds rather than demanding rigid adherence to a failing blueprint. The system isn’t built; it’s coaxed.

The Unfolding Flock

The pursuit of sparse control, as demonstrated by this work, is less a triumph of engineering and more an acknowledgement of inherent system limits. To shepherd a multitude with few is not to solve the problem of collective action, but to sculpt its inevitable chaos. The elegance lies not in prevention of divergence, but in the graceful acceptance – and subtle redirection – of it. Each herder, a carefully placed node in a web of potential failures, predicts the moments when the flock will test the boundaries of control.

Future iterations will inevitably grapple with the fidelity of the mean-field approximation. This simplification, while computationally expedient, masks the individual agonies of each agent nudged from its preferred trajectory. The true cost of control isn’t measured in algorithmic complexity, but in the suppressed degrees of freedom. Further study must confront the question of what is lost when a population is treated as a density, rather than a collection of unique wills.

The work hints at a broader truth: systems don’t yield to control; they evolve within its constraints. The alerts, the interventions – these are not corrections, but data points in a continuous negotiation with the unpredictable. The system isn’t silent when controlled; it’s merely whispering its next potential failure, waiting for the attentive ear that will decode its emergent strategy.

Original article: https://arxiv.org/pdf/2511.21304.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-28 04:59