Disorderly Systems, Linear Insights

Author: Denis Avetisyan

New research reveals a surprisingly simple relationship between structure and vibrational properties in amorphous materials, challenging the need for complex modeling.

A universal linear structure-property relationship (SPR) is established for predicting phonon-related properties of amorphous materials, where atomic configurations are encoded via a symmetry-invariant radial distribution function [latex]RDF_g(r)g(r)[/latex] and mapped to target observables-including phonon density of states, Raman, inelastic neutron scattering, and inelastic X-ray scattering spectra-through learnable weights and biases shared across diverse amorphous systems, encompassing monolayers, bulk glasses, and high-entropy alloys with varying degrees of structural disorder.

A regularized linear model accurately predicts phonon density of states from radial distribution functions in a diverse range of glasses.

Establishing reliable connections between atomic structure and material properties remains a central challenge in understanding glassy materials, yet many data-driven approaches prioritize predictive power over physical interpretability. This work, ‘Beyond overcomplication: a linear model suffices to decode hidden structure-property relationships in glasses’, demonstrates that a surprisingly simple, linear relationship-derived from first-order perturbation theory-can accurately map structural disorder, quantified by the radial distribution function, to vibrational properties like the phonon density of states. This robust connection allows for highly predictive modeling using regularized linear regression across diverse amorphous systems. Does this suggest a fundamental linearity underlying structure-property relationships in disordered materials, potentially simplifying the development of new glass compositions?

Decoding Material Complexity: From Structure to Prediction

The pursuit of accurately predicting a material’s characteristics solely from its atomic structure presents a formidable scientific hurdle. This difficulty doesn’t stem from a lack of fundamental understanding, but rather from the sheer complexity of the interactions between many constituent atoms. While the governing laws of physics – quantum mechanics and electromagnetism – are well-established, solving for the collective behavior of a vast number of interacting particles is computationally intractable for all but the simplest systems. Each atom influences, and is influenced by, every other atom in a complex web of forces, resulting in emergent properties that are difficult to anticipate. These ‘many-body interactions’ introduce subtleties that render straightforward calculations insufficient; a complete description requires accounting for correlations and collective phenomena, demanding increasingly sophisticated theoretical models and computational power to bridge the gap between atomic arrangement and macroscopic behavior.

The Radial Distribution Function (RDF) serves as a remarkably efficient tool for characterizing the arrangement of atoms within a material, effectively distilling complex structural data into a single, interpretable function. Instead of tracking the precise position of every atom – an impractical task for most systems – the RDF focuses on the probability of finding another atom at a given distance from a reference atom. This yields a plot showing the average atomic density as a function of distance, revealing key structural features like nearest-neighbor distances, coordination numbers, and the presence of short- or long-range order. Crucially, the RDF is insensitive to translational symmetry; it describes the structure around an atom, making it ideal for analyzing both crystalline and amorphous materials, and even liquids where long-range order is absent. By providing a fingerprint of atomic connectivity, the RDF offers a powerful means of comparing different materials and predicting their properties, even when detailed atomic positions are unknown.

Establishing a direct correlation between the Radial Distribution Function (RDF) and a material’s vibrational characteristics presents significant hurdles for conventional analytical techniques. Traditional methods often struggle with the inherent complexity of disordered systems, where long-range correlations are weak and the relationship between atomic arrangement and dynamic behavior is not straightforward. These limitations stem from the fact that many established approaches rely on simplifying assumptions about structural perfection or harmonic vibrations, which break down in amorphous or complex materials. Consequently, accurately predicting vibrational properties-such as phonon spectra or thermal conductivity-from RDF data requires innovative methodologies capable of capturing the nuances of structural disorder and anharmonicity, moving beyond simple harmonic approximations and embracing more sophisticated computational or analytical frameworks.

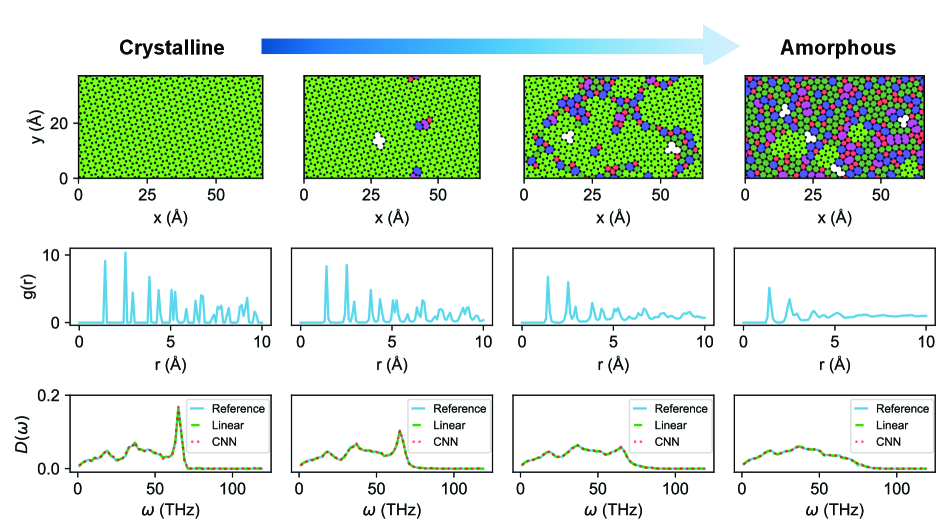
Vibrational characteristics of materials, such as their ability to conduct heat or respond to stress, are profoundly influenced by the degree of atomic-level disorder present within their structure. Perfectly crystalline materials exhibit predictable vibrations, but even slight deviations from perfect order-introduced through defects, amorphous regions, or compositional fluctuations-can drastically alter these modes. Consequently, accurately characterizing this disorder is crucial for predicting a material’s macroscopic behavior. Traditional structural descriptors often fall short in capturing the nuances of such randomness, necessitating the development of robust alternatives capable of quantifying the complexity of atomic arrangements and their impact on vibrational properties. These descriptors must move beyond simple metrics and instead provide a comprehensive representation of the structural landscape, enabling a more accurate correlation between atomic structure and observed material characteristics.

A linear model accurately predicts the structural and electronic properties of increasingly complex disordered materials-including 2D/3D Lennard-Jones, SiC, and CuAlZr-as demonstrated by comparing predicted (dashed curves) and reference (solid curves) radial distribution functions [latex]g(r)[/latex] and density of states (PDOS) with a low test mean squared error (MSE) compared to a convolutional neural network.

Streamlining Material Prediction: A Linear Mapping Approach

Linear Regression is employed to directly correlate the Radial Distribution Function (RDF) with the Phonon Density of States (PDOS), offering a computationally streamlined method for predicting material properties. This approach bypasses the need for complex simulations by establishing a linear mapping between the RDF, which encapsulates the atomic structure, and the PDOS, which characterizes the vibrational modes. The resulting linear model, expressed generally as [latex]PDOS = w \cdot RDF + b[/latex], where ‘w’ represents the weighting coefficients and ‘b’ is the bias term, is determined through a training process utilizing known RDF-PDOS pairs. This simplification allows for rapid property prediction, particularly beneficial when computational resources are limited or a large number of materials need to be screened.

Linear regression mapping of Radial Distribution Functions (RDF) to Phonon Density of States (PDOS) provides a computationally efficient alternative to methods like Density Functional Theory (DFT) or Molecular Dynamics (MD) simulations. Traditional simulations require significant computational resources and time, particularly for large systems or extensive property exploration. This linear approach drastically reduces computational cost by establishing a direct, empirically-derived relationship between the RDF – a representation of atomic structure – and the PDOS, a key determinant of material properties. Consequently, property prediction becomes significantly faster, allowing for rapid screening of materials and exploration of compositional spaces without the expense of detailed simulations. This efficiency is particularly valuable when dealing with large datasets or when iterative design optimization is required.

The accuracy of the linear mapping between the Radial Distribution Function (RDF) and the Phonon Density of States (PDOS) is fundamentally dependent on the RDF’s representation of the material’s atomic structure. Any inaccuracies or artifacts present in the RDF, arising from data collection or processing limitations, will directly propagate to the predicted PDOS. Specifically, the RDF must precisely capture interatomic distances and coordination numbers; deviations from the true atomic arrangement will result in an inaccurate mapping and, consequently, an erroneous prediction of phonon behavior. Therefore, careful consideration of the RDF generation process – including data resolution, noise reduction techniques, and appropriate modeling of atomic vibrations – is crucial for ensuring the reliability of the linear regression approach.

A comparative analysis was conducted between the linear regression method and a Deep Convolutional Neural Network (CNN) to assess the efficiency of the simplified approach. Results demonstrate that, particularly when utilizing limited datasets, the linear regression model achieves performance metrics comparable to those of the CNN. This suggests that the linear mapping technique offers a computationally advantageous alternative to more complex machine learning models, delivering predictive accuracy without requiring extensive computational resources or large training datasets. The benchmark comparison highlights the linear approach’s effectiveness in scenarios where data availability is a constraint.

A learned linear mapping of amorphous monolayer carbon reveals a correspondence between structural features-indicated by the reference radial distribution function (RDF) and density of states (PDOS)-and learned weights visualized as a heatmap with [latex]\alpha=10^{-5}[/latex] and [latex]\beta=0[/latex] regularization.

Validating Predictive Power: Diverse Materials and Robustness

To evaluate the model’s ability to generalize beyond the training dataset, we performed calculations on Silicon Carbide (SiC). This material was modeled using a Machine-Learned Interatomic Potential (MLIP), allowing us to assess performance on a system with differing atomic interactions and structural characteristics compared to those used during training. The utilization of an MLIP for SiC provides a crucial test of the framework’s transferability, as these potentials are specifically trained to represent the many-body interactions within a material and can exhibit varying degrees of accuracy when applied to novel compositions or structures. This assessment helps determine the model’s robustness and its potential for application to a wider range of materials beyond the initial training set.

The model’s validation extended to a Copper Aluminum Zirconium alloy, utilizing an Embedded-Atom Method potential to accurately represent the material’s many-body interactions. This approach allows for a more realistic simulation of atomic behavior compared to pairwise potentials. Quantitative performance on this alloy yielded a Mean Squared Error (MSE) of approximately 2×10^-5. This level of accuracy is comparable to that achieved by Convolutional Neural Network (CNN) based approaches for similar materials modeling tasks, demonstrating the framework’s competitive performance and suitability for complex alloy systems.

A periodic Lennard-Jones (LJ) system was utilized as a baseline validation case due to its analytically defined potential energy surface and readily available reference data. This allows for a controlled evaluation of the model’s ability to accurately predict system behavior without the complexities introduced by more sophisticated interatomic potentials or material compositions. The LJ potential, defined as [latex]V(r) = 4\epsilon \left[ \left( \frac{\sigma}{r} \right)^{12} – \left( \frac{\sigma}{r} \right)^{6} \right][/latex], provides a simple yet non-trivial test of the model’s capacity to capture short-range repulsive and long-range attractive interactions, establishing a foundational performance metric against which results from more complex systems can be compared.

Validation of the model’s predictions is performed through comparison with Spectroscopic Measurements, specifically those that directly probe the Phonon Density of States (PDOS). These measurements provide experimental data regarding the vibrational modes of the material, allowing for a quantitative assessment of the model’s accuracy in predicting these modes. Discrepancies between the predicted PDOS and the experimentally obtained PDOS are used to identify areas for model refinement and to gauge the overall reliability of the framework in characterizing material vibrational properties. This direct comparison ensures the model’s predictions are grounded in physical reality and are not merely artifacts of the computational approach.

Analysis of amorphous material configurations-ranging from crystalline to highly disordered-reveals how ring statistics (visualized with a color scheme denoting six-membered rings in green, five-membered in red, seven-membered in blue, and eight/nine-membered in purple) correlate with predicted density of states (PDOS) obtained via linear modeling and convolutional neural networks, demonstrating model performance across varying degrees of structural disorder.

Expanding the Horizon: Topology-Informed Materials Design

The predictive model was deliberately broadened to encompass Amorphous Monolayer Carbon, a material distinguished by its inherent structural disorder. Unlike crystalline materials with repeating patterns, amorphous carbon exhibits a randomized atomic arrangement, significantly influencing its physical properties. This introduces a considerable challenge for property prediction, as traditional methods relying on periodicity become ineffective. By applying the framework to this disordered system, researchers demonstrate the model’s adaptability beyond ideal crystalline structures and its potential to address the complexities present in real-world materials. The success in characterizing amorphous carbon validates the approach as a robust tool for materials discovery, even when dealing with significant deviations from perfect order.

Persistent Homology offers a powerful means of characterizing the intricate structural features present in disordered materials. Unlike traditional methods that rely on specific geometric properties, this topological descriptor focuses on the connectivity of a material, identifying loops, voids, and connected components regardless of their precise shape or size. By tracking these features across multiple scales, Persistent Homology generates a ‘barcode’ – a visual representation of the material’s topological signature – that is remarkably sensitive to even subtle changes in structure. This allows for the quantification of disorder, capturing information about the arrangement of atoms or molecules in a way that is invariant to continuous deformations, providing a robust and insightful tool for materials characterization and prediction of related properties.

The prediction of thermal conductivity, a material property dictated by how efficiently vibrations propagate, is significantly advanced through the integration of Persistent Homology and Ridge Regression. Persistent Homology, a technique from topological data analysis, effectively quantifies the complex structural features of a material, capturing information about connectivity and voids that influence vibrational modes. By pairing these topological descriptors with the statistical modeling power of Ridge Regression, researchers demonstrate a robust method for predicting thermal conductivity directly from structural data. This approach bypasses computationally expensive simulations of atomic vibrations, offering a streamlined pathway toward materials discovery and design where thermal properties can be estimated with high accuracy and minimal computational cost, opening doors to the rapid screening of novel materials with tailored thermal characteristics.

The predictive power of this novel approach is demonstrated by its remarkably low training loss of 1.7×10^-6, a figure directly comparable to the performance of Convolutional Neural Networks – which achieved a loss of 1.4×10^-6 in the same predictive task. This parity in accuracy, achieved through a topologically-informed machine learning framework, suggests a computationally efficient alternative for materials design. By directly correlating structural data with material properties, such as thermal conductivity, the methodology bypasses the need for intensive simulations, offering a pathway to rapidly screen and identify materials with desired characteristics – effectively enabling the prediction of properties from structure alone and accelerating the discovery of novel materials.

The study reveals a fundamental simplicity underlying the complexity of amorphous materials, demonstrating that a linear model can effectively decode structure-property relationships. This finding echoes Albert Camus’s assertion: “The essential is invisible to the eye.” While machine learning often pursues intricate, non-linear solutions, this work suggests that the core principles governing the vibrational properties of glasses-as represented by the radial distribution function-are surprisingly direct. Scalability without ethics, or in this case, model complexity without justification, leads toward chaos; the researchers prioritized parsimony, and uncovered a fundamental truth about disordered systems – a linear connection between structure and phonon density of states.

Beyond Simplicity: Charting a Course Forward

The demonstrated efficacy of a linear model in decoding the structure-property relationships of amorphous materials presents a challenge to the prevailing trend of increasingly complex algorithmic solutions. It suggests that the field has, perhaps, been overly eager to embrace computational sophistication at the expense of conceptual clarity. The persistence of a surprisingly linear relationship, even within disordered systems, compels a reevaluation of the assumptions embedded within more elaborate models-assumptions that often lack explicit justification. The temptation to automate complexity should be tempered by a recognition that the simplest explanation, adequately supported, remains the most valuable.

Future work must address the limits of this linearity. To what extent does this model break down as material complexity increases – specifically, with the introduction of multiple chemical species or higher-order structural motifs? Furthermore, the model currently relies on the radial distribution function as input; exploring alternative, or complementary, structural descriptors could reveal additional linear relationships previously obscured. Crucially, research should not solely focus on predictive accuracy, but also on the interpretability of the model’s parameters – revealing the underlying physical mechanisms governing these materials.

Ultimately, this work serves as a cautionary tale. Technology that scales but erodes trust in fundamental understanding is unworthy of deployment. The values are encoded in code, even unseen. A deeper investigation into these surprisingly simple relationships may not only advance materials science, but also remind the field that progress isn’t always synonymous with increasing complexity.

Original article: https://arxiv.org/pdf/2602.05313.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Decoding Material Complexity: From Structure to Prediction

Streamlining Material Prediction: A Linear Mapping Approach

Validating Predictive Power: Diverse Materials and Robustness

Expanding the Horizon: Topology-Informed Materials Design

Beyond Simplicity: Charting a Course Forward

See also: