Charting a Faster Course: Multi-Graph Search for Robot Navigation

Author: Denis Avetisyan

A new motion planning framework dramatically improves efficiency by simultaneously exploring multiple potential paths for robots operating in complex, high-dimensional spaces.

The system generates navigable environments represented as occupancy grids-used to compute attractive forces during path planning-and successfully demonstrates its capabilities beyond robotic manipulation by autonomously charting a course through a complex three-dimensional space.

This work introduces a multi-graph search (Mgs) approach with workspace attractors, guaranteeing completeness and bounded suboptimality for robot motion planning.

Efficiently planning motions for complex robotic systems remains a challenge, often requiring a trade-off between computational cost, solution quality, and reliability. This paper introduces Multi Graph Search for High-Dimensional Robot Motion Planning, a novel search-based algorithm that simultaneously explores multiple implicit graphs within the state space, guided by strategically positioned ‘attractors’ to accelerate convergence. By merging initially disconnected subgraphs as the search progresses, MGS achieves completeness and bounded suboptimality, demonstrated through benchmarks on manipulation and mobile manipulation tasks. Could this multi-graph approach unlock new possibilities for real-time, robust robot control in dynamic environments?

The Inevitable Complexity of Motion

Traditional motion planning algorithms, while foundational, encounter significant hurdles when applied to realistic scenarios involving numerous degrees of freedom and intricate limitations. As the dimensionality of a robot’s configuration space increases – for instance, with more joints or a complex environment – the computational cost of searching for a viable path escalates exponentially. This phenomenon, often referred to as the “curse of dimensionality,” means that even modestly complex robots operating in cluttered spaces can quickly overwhelm conventional planning methods. Moreover, real-world constraints – such as joint limits, obstacle avoidance, and dynamic stability – further complicate the search process, demanding algorithms capable of handling non-linearities and intricate dependencies. Consequently, finding collision-free paths that satisfy all constraints becomes computationally intractable, necessitating the development of more sophisticated and efficient planning techniques.

The search for collision-free paths for robots and other autonomous systems rapidly escalates in complexity as scenarios become more realistic. This computational intractability arises because the number of possible configurations-all the possible positions and orientations a system can adopt-grows exponentially with the number of degrees of freedom. For example, a robotic arm with seven joints doesn’t just need to avoid obstacles in three-dimensional space; it must simultaneously coordinate the angle of each joint, creating a vast configuration space to search. Consequently, even moderately complex environments can overwhelm traditional planning algorithms, requiring prohibitive amounts of time and computational resources to determine a feasible path, if one exists at all. This limitation underscores the critical need for methods that can intelligently navigate these high-dimensional spaces and efficiently identify viable solutions without succumbing to the “curse of dimensionality.”

The difficulty in navigating complex environments stems from the sheer scale of the configuration space – the complete set of possible positions and orientations for a robotic system. Traditional motion planning algorithms often employ techniques that become increasingly inefficient as this space grows, leading to exponential increases in computation time. These methods typically sample or search this space in a manner that doesn’t adequately account for the geometry of the environment or the constraints imposed on the robot’s movement. Consequently, a significant portion of the explored space proves irrelevant, while potentially viable paths remain undiscovered. This inefficient exploration hinders real-time performance and limits the applicability of these algorithms to scenarios involving numerous degrees of freedom or intricate obstacles, demanding novel strategies for intelligently traversing and mapping these vast landscapes.

Addressing the limitations of current motion planning algorithms demands a shift toward strategies that intelligently reconcile the desire for optimal solutions with the practical realities of computational cost. Researchers are actively investigating techniques like sampling-based planners with enhanced exploration strategies, learning-based approaches that leverage data to predict successful paths, and hierarchical planning methods that decompose complex problems into more manageable sub-problems. These innovative avenues prioritize not simply finding a solution, but discovering one within a reasonable timeframe, even amidst high-dimensional spaces and intricate constraints. The goal is to achieve a pragmatic balance-accepting a slightly suboptimal path if it dramatically reduces computation time, thereby enabling real-time applications in robotics, virtual reality, and autonomous systems.

Across ten perturbed versions of each task, the coefficient of variation (CV) of path costs and planning times demonstrates consistent performance for both manipulation and mobile manipulation planners.

Expanding the Search: A Multi-Directional Approach

Multi-directional search algorithms enhance exploration of the search space by simultaneously expanding frontiers from multiple starting points. Unlike traditional unidirectional searches that progress solely from an initial state, these methods initiate searches from both the start and goal states, or from multiple intermediate points. This parallel expansion effectively reduces the overall search distance as the search progresses from multiple directions, increasing the probability of rapidly identifying a solution path. The simultaneous advancement from multiple fronts allows the algorithm to cover more ground in a given timeframe, thereby improving the efficiency of path planning and problem-solving in complex environments.

Bidirectional Search and Rapidly-exploring Random Tree-Connect (RRT-Connect) represent key implementations of multi-directional search strategies. Bidirectional Search operates by simultaneously growing search trees from both the start and goal states, attempting to connect them as quickly as possible; this effectively halves the maximum search depth compared to unidirectional approaches. RRT-Connect, similarly, builds trees from both ends, but utilizes random sampling and connection attempts to efficiently explore the configuration space. Both methods prioritize connecting the trees, and success is determined when a path is found linking the start and goal nodes, thereby completing the search process.

The acceleration of path planning achieved by multi-directional search techniques stems from a reduction in the effective search distance. Traditional unidirectional algorithms explore the state space outward from a single starting point, potentially requiring examination of exponentially growing areas. By simultaneously expanding search frontiers from both the start and goal states – as exemplified by Bidirectional Search and RRT-Connect – these algorithms meet “in the middle,” effectively halving the maximum search depth required to find a solution. This reduction isn’t strictly linear; the algorithms avoid redundant exploration of shared state space, leading to a more substantial decrease in computational effort, particularly in high-dimensional or complex environments. The convergence rate is dependent on the branching factor and the overlap between the forward and reverse search spaces.

Combining information from multiple search fronts involves simultaneously expanding the search from one or more starting points and, often, from the goal state as well. This contrasts with unidirectional search, which expands solely from the start. By propagating information bidirectionally, or from multiple exploratory paths, the algorithm effectively reduces the search space. The intersection or connection of these search fronts represents a solution path. This approach leverages the principle that the combined distance covered by multiple searches can be less than the distance covered by a single search to reach the same goal, leading to faster path planning and improved efficiency in complex environments.

Forward attractor discovery consistently generates attractors oriented towards the goal, unlike backward attractors which frequently face away, as illustrated by the white circle marking attractors discovered during policy rollout with the search root highlighted in yellow.

Guiding the Search: The Illusion of Foresight

Subgoal guidance is a search strategy that decomposes a complex planning problem into a sequence of simpler, intermediate goals. By defining these subgoals, the search algorithm can focus its exploration on configurations that incrementally satisfy these objectives, rather than directly attempting to reach the final goal state. This approach reduces the search space and improves efficiency, particularly in high-dimensional configuration spaces. The selection of appropriate subgoals is crucial; they should be both achievable and relevant to the overall task, providing a measurable progression towards the desired solution. Effectively, subgoal guidance transforms a single, potentially intractable search problem into a series of manageable steps.

Workspace attractors function as guiding points within the robot’s configuration space, influencing the search process by biasing exploration towards promising regions. These attractors are defined locations in the workspace that the planning algorithm attempts to approach, effectively shaping the search tree and concentrating computational effort around feasible solutions. By strategically positioning attractors, the planner can avoid exploring irrelevant or unreachable configurations, leading to improved efficiency and a reduced search space. The density and distribution of attractors directly impact the planner’s ability to quickly discover valid paths, with closer attractors exerting a stronger influence on the trajectory generation process.

Multi-Graph Search (Mgs) constructs a search graph by utilizing workspace attractors as nodes, enabling exploration in multiple directions simultaneously. Unlike traditional single-graph approaches, Mgs builds connections between these attractor nodes, forming a multi-directional graph that allows the planner to pursue several potential solution paths concurrently. This is achieved by establishing edges representing feasible transitions between attractors, with search proceeding outward from the initial attractor until a goal state is reached. The resulting graph structure facilitates a more comprehensive and efficient exploration of the configuration space, as the planner is not constrained to a single path but can dynamically switch between attractor-based sub-graphs.

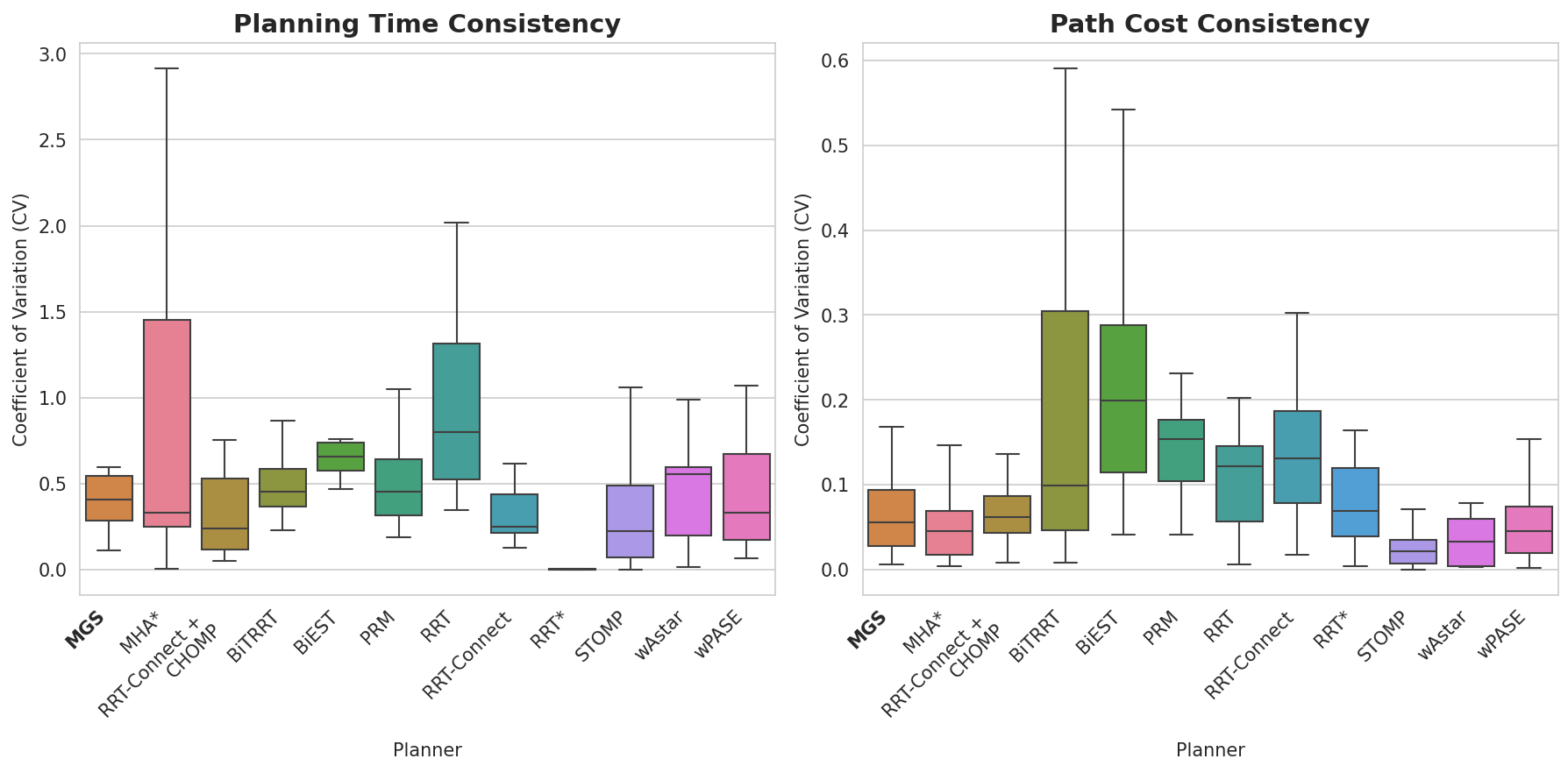
The Multi-Graph Search (Mgs) framework achieves success rates comparable to those of current state-of-the-art planning algorithms. Crucially, Mgs exhibits more predictable performance characteristics; quantitative analysis demonstrates a lower Coefficient of Variation (CV) of path costs when compared to typical sampling-based motion planning methods. A lower CV indicates less variance in solution cost, meaning Mgs consistently finds solutions of similar quality across multiple trials, whereas sampling-based planners may yield significantly varying path costs even with identical problem instances. This improved predictability is a key benefit for applications requiring reliable performance and consistent solution quality.

Attractor states [latex]A_i[/latex] and their trivially connected regions define reachable states via greedy tracing, originating from a seed state (red) expanded using a breadth-first search with cardinal cost 1, diagonal cost [latex]2\sqrt{2}[/latex], and Euclidean distance as a potential.

The Balance: Efficiency Versus Perfection

Motion planning frequently leverages the distinct advantages of search-based and sampling-based techniques. Search-based planners, akin to navigating a map, systematically explore possible paths using graph search algorithms, guaranteeing optimality but often struggling in high-dimensional spaces. Conversely, sampling-based methods, such as Probabilistic Roadmaps (PRM) and Rapidly-exploring Random Trees (RRT), efficiently explore configuration spaces by randomly sampling points, excelling in complex environments but offering no guarantee of finding the shortest or most efficient path. The synergy arises when these approaches are combined; sampling-based methods can generate an initial feasible trajectory, which is then refined by the precision of a search-based planner, or a search-based planner can intelligently guide the sampling process, reducing exploration time and improving solution quality. This complementary relationship allows for robust and efficient motion planning in a wide range of robotic applications, balancing the need for both speed and optimality.

Optimization-based methods represent a powerful approach to refining initial trajectories, pushing beyond simple feasibility towards genuinely improved performance metrics. Algorithms like STOMP (Stochastic Trajectory Optimization for Motion Planning) and CHOMP (Covariant Hamiltonian Optimization for Motion Planning) achieve this by iteratively adjusting trajectory parameters to minimize a cost function that encapsulates desired qualities – such as smoothness, energy expenditure, or proximity to obstacles. Unlike sampling-based or search-based planners which often prioritize finding a solution, these optimization techniques focus on sculpting an existing solution into an optimal one, leveraging gradient-based methods to navigate the space of possible trajectories. This refinement process often involves defining a cost function that penalizes deviations from ideal behavior, and then employing numerical optimization techniques to minimize this cost – resulting in smoother, faster, and more efficient motions, even with complex constraints.

Effective motion planning relies heavily on the strategic implementation of heuristic functions, which serve as guiding principles during the search for optimal paths. These functions estimate the cost of reaching a goal from a given state, allowing algorithms to prioritize exploration of more promising avenues and avoid exhaustive, computationally expensive searches. Crucially, a well-designed heuristic doesn’t just accelerate the planning process; it guarantees a level of solution quality, ensuring the resulting path remains within a defined margin of optimality – known as bounded suboptimality. While a perfect heuristic would yield the absolute best solution, practical constraints necessitate a balance; a slightly imperfect, yet computationally efficient, heuristic can deliver acceptable performance with predictable resource usage, making it a cornerstone of robust and scalable motion planning systems.

The Mgs framework demonstrates a crucial advantage in computational efficiency, exhibiting a linear scaling of overhead with the increasing number of sub-graphs utilized. This predictable relationship between computational cost and performance is vital for real-world applications, allowing planners to reliably estimate resource demands and adjust the granularity of the search space. Unlike methods with exponential scaling, Mgs maintains a consistent and manageable computational burden, even as problem complexity increases, effectively enabling a tunable balance between solution quality and processing time. This linear scalability positions Mgs as a practical solution for complex motion planning scenarios where consistent performance and resource predictability are paramount.

Path cost consistency, measured by the coefficient of variation across five trials, demonstrates that the planner achieves repeatable performance on both manipulation and mobile manipulation tasks.

Towards Adaptation: The Future of Intelligent Planning

Planning systems traditionally rely on hand-crafted algorithms and explicitly defined rules, limiting their ability to cope with unforeseen circumstances or intricate environments. However, learning-based methods present a paradigm shift, allowing robots and artificial intelligence to acquire planning strategies through experience-much like humans do. By leveraging techniques such as reinforcement learning and imitation learning, these systems can analyze past successes and failures, gradually refining their approach to problem-solving. This experiential learning enables adaptation to novel situations without requiring explicit reprogramming, fostering a level of flexibility previously unattainable. The potential extends beyond simply reacting to change; these methods allow systems to proactively improve their planning abilities, optimizing for efficiency and robustness over time and promising a future where intelligent agents can navigate complexity with increasing skill.

Adaptive planning systems are emerging from the integration of machine learning with established search algorithms and heuristic methods. These systems move beyond pre-programmed responses by learning from past experiences to refine planning strategies. Multi-directional search allows exploration of numerous potential pathways concurrently, while heuristics provide informed guidance, prioritizing promising avenues and accelerating the discovery of optimal solutions. This synergy enables robots and autonomous agents to dynamically adjust to unforeseen circumstances and novel environments, effectively learning to plan not just how to achieve a goal, but how to learn to plan more efficiently over time, ultimately fostering resilience and intelligence in complex scenarios.

Successfully translating advanced planning algorithms from controlled laboratory settings to unpredictable real-world scenarios demands significant attention to generalization and robustness. Current systems often struggle when confronted with novel situations, slight variations in environmental conditions, or unexpected obstacles not encountered during training. Researchers are actively exploring techniques like domain randomization – deliberately introducing variability during the learning process – and meta-learning, which enables algorithms to learn how to learn, to improve adaptability. Furthermore, ensuring robustness requires developing planning systems resilient to sensor noise, imperfect state estimation, and even adversarial perturbations. Overcoming these hurdles is not merely a matter of incremental improvement; it represents a fundamental shift towards truly intelligent systems capable of reliable, autonomous operation in complex and ever-changing environments.

The convergence of learning-based methods with advanced search techniques heralds a new era in robotic navigation. These intelligent systems don’t simply follow pre-programmed routes; instead, they dynamically adapt to unforeseen obstacles and changing conditions within complex environments. By learning from past experiences and integrating that knowledge with real-time sensory input, robots can formulate and execute plans with remarkable efficiency. This synergistic approach enables them to explore unfamiliar terrains, optimize routes for energy conservation, and respond effectively to dynamic challenges – ultimately promising robots that move through the world with a level of adaptability previously unattainable, and opening doors for applications ranging from autonomous delivery to disaster response and space exploration.

“`html

The pursuit of efficient motion planning, as detailed in this framework, echoes a fundamental truth about complex systems. Every dependency-each algorithmic choice in the Mgs framework, every attractor placed within the workspace-is a promise made to the past, a commitment to a specific trajectory of solutions. The system doesn’t simply solve a problem; it propagates constraints, negotiating the tension between completeness and bounded suboptimality. As Tim Berners-Lee observed, “The web is more important than any single application running on it.” Similarly, the Mgs framework isn’t merely about finding a path, but establishing a robust, adaptable ecosystem for navigating high-dimensional spaces, anticipating future demands and, inevitably, fixing itself as challenges arise.

The Road Ahead

This multi-graph search, with its careful placement of workspace attractors, feels less like a solution and more like a temporary reprieve. The guarantees of completeness and bounded suboptimality are comforting, certainly, but they mask a fundamental truth: every deployment is a small apocalypse. The complexity simply shifts. Future work will undoubtedly focus on adaptive attractor placement – letting the robot ‘learn’ where to look – but that invites a different class of failure. What begins as guidance inevitably becomes a constraint, a new local minimum in the search space.

The real challenge isn’t efficiency, but resilience. Current approaches assume a static world, a known cost function. A truly robust system will need to account for the unexpected, for changes in the environment that invalidate the carefully constructed graphs. This means embracing uncertainty, perhaps through probabilistic planning or reinforcement learning, but also accepting that perfect solutions are rarely, if ever, attainable.

No one writes prophecies after they come true. The focus will inevitably shift from theoretical guarantees to empirical performance, from proving completeness to demonstrating robustness in the face of real-world chaos. And, as always, the simplest path will likely remain the most elusive.

Original article: https://arxiv.org/pdf/2602.12096.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/