Building Better Brains: How to Teach AI to Reason More Effectively

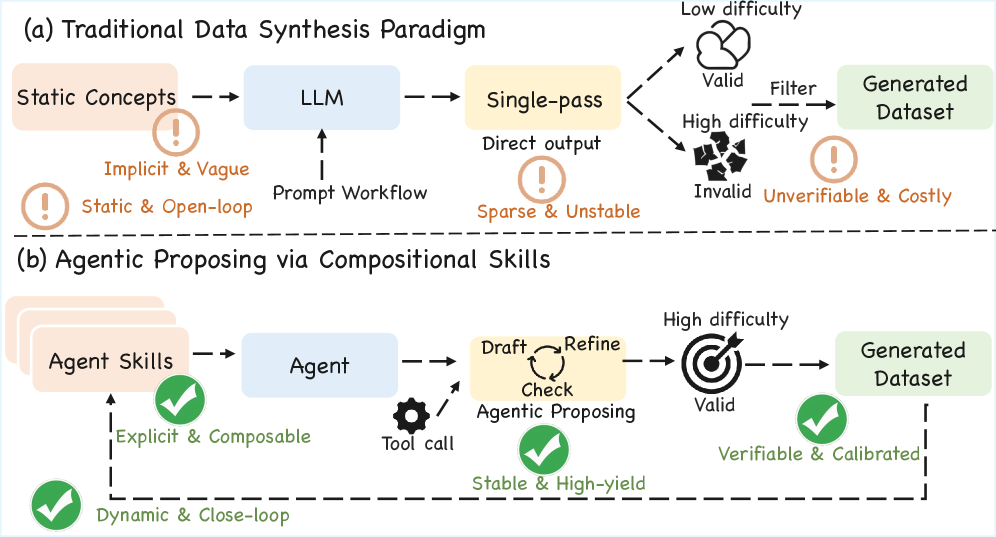
Author: Denis Avetisyan

Researchers have developed a new method for creating increasingly complex reasoning problems to better train artificial intelligence systems.

The framework synthesizes complex problem-solving capabilities through a three-stage process-skill acquisition from diverse data, agentic supervised fine-tuning mirroring expert reasoning with dynamic skill pruning, and multi-granularity reinforcement learning-guided by a structured reasoning flow [latex]Draft \to Check \to Refine \to Finalize[/latex] and curriculum-based skill distribution to generate challenging problems for downstream solver training.

Agentic Proposing synthesizes training data by composing skills into complex problems, improving performance via multi-granularity policy optimization and reinforcement learning.

Achieving robust complex reasoning in large language models is hampered by the scarcity of high-quality, scalable training data. This limitation motivates ‘Agentic Proposing: Enhancing Large Language Model Reasoning via Compositional Skill Synthesis’, which introduces a novel framework for automatically generating challenging and verifiable reasoning problems. By modeling problem synthesis as a goal-driven sequential decision process-where an agent iteratively composes modular skills-the approach yields synthetic datasets that significantly outperform those created by existing methods. Could this paradigm of agentic data synthesis unlock a new era of efficient and effective LLM training, diminishing reliance on costly human annotation?

The Challenge of Insightful Problem Generation

Many current automated systems for generating mathematical problems struggle to produce exercises that are genuinely insightful or demanding. Often, these systems rely on superficial manipulations of equations or keywords, leading to problems that are either trivially solvable with minimal understanding, or contain logical flaws rendering them unsolvable as intended. This limitation stems from a lack of deep reasoning capabilities; the algorithms frequently fail to grasp the underlying mathematical principles and instead generate content based on pattern matching rather than conceptual coherence. Consequently, the resulting problems often lack the nuanced structure and logical connections characteristic of well-designed mathematical exercises, hindering their effectiveness as tools for learning and assessment. The systems often generate problems that are syntactically correct but semantically meaningless or uninteresting, highlighting the need for more sophisticated approaches that prioritize mathematical validity and conceptual depth over simple generation techniques.

Simply increasing the size of existing language models proves inadequate for crafting genuinely challenging mathematical problems. These models, while adept at pattern recognition and text generation, lack the inherent capacity for rigorous logical deduction and verification crucial for problem construction. A more effective strategy necessitates a structured approach, one that explicitly incorporates reasoning engines and formal verification techniques. This involves not merely generating problem statements, but also independently confirming their validity, exploring multiple solution pathways, and assessing the logical complexity of each step. Such a system would move beyond superficial difficulty, ensuring generated problems demand genuine problem-solving skills and aren’t solvable through accidental pattern matching or statistical likelihoods – ultimately leading to exercises that truly test and enhance mathematical understanding.

Generating mathematical problems automatically presents a significant calibration challenge: crafting exercises that are neither instantly solvable nor impossibly complex. Simply increasing problem parameters doesn’t guarantee difficulty; a problem may appear lengthy or involve numerous steps without demanding genuine insight. Conversely, a deceptively simple problem can pose a considerable challenge if it requires a non-obvious application of core principles. Achieving this ‘sweet spot’ necessitates a nuanced understanding of cognitive load and problem-solving strategies, demanding that generated problems are carefully tuned to align with a target skill level. This requires systems to not only construct problems but also to implicitly assess their cognitive demands, potentially through simulations of human problem-solving processes or by leveraging established metrics of mathematical complexity, such as [latex] \text{Kolmogorov complexity} [/latex], to predict solvability.

Agentic proposing, a closed-loop system composing modular skills with tool-assisted verification, offers a stable and verifiable alternative to traditional, open-loop data synthesis methods which often produce unstable and unverifiable results.

Decomposition and the Agentic Framework

Agentic Proposing utilizes a decomposition strategy wherein the complex task of problem construction is broken down into discrete, reusable agent skills. This modularity facilitates scalability by allowing for the independent development, testing, and refinement of individual skills. The framework defines these skills as composable units, meaning they can be combined and sequenced in various configurations to address diverse problem-creation challenges. This approach contrasts with monolithic problem construction methods, offering increased flexibility and reducing the complexity associated with maintaining and adapting the system. By isolating functionality into these composable skills, the Agentic Proposing framework enables efficient resource allocation and promotes code reuse, ultimately lowering the barrier to entry for building complex problem-solving agents.

Agentic Proposing utilizes a Partially Observable Markov Decision Process (POMDP) to formally represent the problem construction process as a sequential decision-making problem under uncertainty. The POMDP models the agent’s belief state regarding the logical consistency and complexity of the developing problem, factoring in incomplete information derived from internal reflection and tool-use. Specifically, the state space represents potential problem formulations, actions involve proposing new problem elements or modifications, the transition function models the effect of these actions on problem consistency and complexity, and the reward function quantifies the desirability of a given problem state based on these factors. By framing problem creation as a POMDP, the framework enables the agent to strategically explore the space of possible problems, balancing logical validity with desired levels of complexity through probabilistic reasoning and optimal decision-making.

The agentic framework utilizes an iterative process of internal reflection and tool-use to enhance reasoning validity. This workflow involves the agent systematically evaluating its own intermediate reasoning steps – the internal reflection – and then employing external tools to verify these steps and confirm logical consistency. Tool-use extends beyond simple calculation; it encompasses accessing knowledge bases, executing code for simulation, and leveraging formal verification methods. This cycle of self-evaluation and external validation is repeated throughout the problem construction process, allowing the agent to identify and correct errors, refine its approach, and ultimately increase the reliability of its proposed solutions. The frequency and type of tool utilized are dynamically adjusted based on the agent’s confidence level and the complexity of the current reasoning step.

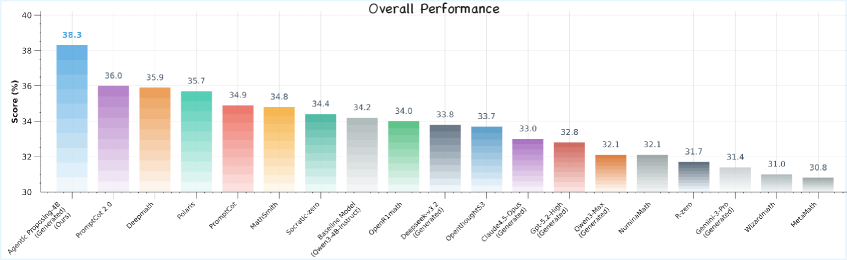
Proposing-30B-A3B achieves state-of-the-art accuracy of 91.6% on AIME 2025, demonstrating superior parameter efficiency by outperforming open-source models with up to 20[latex] imes[/latex] more parameters and rivaling top proprietary models.

Refining Decision-Making Through Policy Optimization

Multi-granularity policy optimization refines the agent’s decision-making process by integrating both terminal and process rewards during training. Terminal rewards are received upon completion of a task, providing a sparse signal for evaluating overall success. Process rewards, conversely, are assigned at each step based on intermediate progress and adherence to desired behaviors. This combination addresses the challenges of sparse reward environments common in complex reasoning tasks; process rewards offer a denser, more frequent signal to guide learning, while terminal rewards ensure alignment with the ultimate objective. The weighting of these reward signals is dynamically adjusted to optimize for both short-term progress and long-term goal achievement, accelerating convergence and improving policy performance.

Advantage estimation serves as a critical refinement of standard reinforcement learning techniques by providing a more precise signal for policy updates. Rather than solely relying on cumulative rewards, this method calculates the advantage of taking a specific action in a given state, relative to the expected return from following the current policy. This is typically achieved using techniques like Generalized Advantage Estimation (GAE), which balances bias and variance in the estimation. For complex reasoning tasks, where rewards may be sparse or delayed, a detailed advantage function significantly improves learning efficiency by clarifying which actions contribute positively to long-term success and enabling the agent to differentiate between beneficial and detrimental steps, even in ambiguous situations.

The agent’s policy is initialized via supervised fine-tuning, leveraging a dataset of expert trajectories to establish a functional base policy before reinforcement learning begins. This pre-training phase accelerates learning and improves sample efficiency. Subsequently, curriculum learning is implemented to prioritize training on tasks or states where the agent demonstrates the lowest performance. This iterative process focuses learning efforts on areas requiring the most improvement, mitigating the challenges associated with sparse rewards and complex reasoning by systematically addressing weaknesses in the agent’s capabilities.

Using a training budget of 10,000 trajectories and a consistent GRPO recipe, the methods achieve varying Mean@64 accuracies across benchmarks, with arrows indicating absolute changes relative to zero-shot performance.

Validation and Performance on AIME 2025

The agent’s capacity to generate high-quality mathematical problems was rigorously assessed using the challenging AIME 2025 benchmark, resulting in a state-of-the-art accuracy of 91.6%. This performance signifies a substantial advancement in automated problem creation, exceeding the capabilities of previously established models. The benchmark’s difficulty lies not only in ensuring correct mathematical formulations but also in producing problems that demand genuine reasoning skills – a criteria on which the agent demonstrably excels. This level of accuracy indicates a system capable of consistently generating problems that are both logically sound and appropriately challenging for advanced mathematical students, marking a significant step towards automated educational tools and research in mathematical problem-solving.

The generation of effective mathematical problems hinges on maintaining strict logical consistency, and this agent prioritizes that crucial element. Unlike systems prone to introducing subtle errors or ambiguous phrasing, this model employs a rigorous verification process to ensure each problem’s solution pathway is both sound and uniquely determined. This commitment to logical integrity isn’t merely about avoiding incorrect answers; it directly impacts the quality of assessment. Problems lacking internal consistency fail to accurately gauge a student’s true mathematical reasoning abilities, instead testing for pattern recognition or error detection. By consistently producing logically sound problems, the agent offers a more reliable and insightful evaluation of mathematical skill, allowing for precise identification of strengths and weaknesses in problem-solving approaches – a feature demonstrably superior to benchmarks that prioritize quantity over quality in problem generation.

Rigorous evaluation demonstrates this agent’s superior capabilities in automated mathematical problem generation when contrasted with current state-of-the-art methodologies. Comparative analyses consistently reveal performance gains over established models such as DeepSeek-Math, not only in ensuring the logical validity of generated problems but also in crafting challenges of greater complexity. This approach achieves a level of performance that closely rivals that of significantly larger language models, including GPT-5 and Gemini-3-Pro, suggesting a more efficient and targeted strategy for creating high-quality mathematical content. The ability to match or exceed the performance of these models while potentially requiring fewer computational resources positions this agent as a promising advancement in the field of automated mathematical reasoning and problem creation.

Towards Dynamic Learning and Advanced Assessment

The architecture facilitates genuinely adaptive learning environments by dynamically adjusting problem complexity based on a student’s demonstrated proficiency. Rather than presenting a static sequence of challenges, the system continually assesses performance and generates new problems calibrated to the individual’s current skill level – increasing difficulty upon success and offering simpler variations when a student struggles. This personalization is achieved through a generative model that doesn’t simply select from a pre-defined bank of questions, but instead creates novel problems on demand, ensuring a continuous stream of appropriately challenging material. This approach moves beyond one-size-fits-all instruction, fostering deeper understanding and maximizing learning potential by keeping students consistently engaged at the edge of their capabilities.

Automated problem generation promises a transformative shift in education by alleviating the substantial workload currently placed on instructors. Traditionally, crafting diverse and appropriately challenging exercises requires significant time and effort; this system offers a pathway to dynamically create problems tailored to each student’s evolving skill level. This isn’t simply about creating more practice questions, but about constructing learning experiences that adapt in real-time, offering increasingly complex challenges as proficiency grows and providing targeted support where needed. The result is a personalized learning journey for every student, freeing educators to focus on mentorship, nuanced instruction, and fostering deeper conceptual understanding, rather than being overwhelmed by the logistical demands of problem creation.

The development of this adaptive learning framework is not intended as a closed system, but rather as a springboard for broader applications and deeper learning capabilities. Researchers are actively investigating the transfer of the agent’s problem-solving skills to new domains, including the complexities of physics and the logical structures of computer science. This expansion requires overcoming challenges in representing domain-specific knowledge and adapting the agent’s reasoning processes accordingly. Simultaneously, efforts are underway to move beyond simple skill mastery and explore more nuanced methods for skill acquisition, such as meta-learning and curriculum learning, which allow the agent to learn how to learn and optimize its own learning path – ultimately paving the way for truly intelligent and self-improving educational tools.

The pursuit of robust intelligence, as demonstrated by Agentic Proposing, necessitates a careful consideration of systemic integrity. This framework, with its decomposition of problem construction into composable skills, implicitly acknowledges that a system’s behavior is dictated by its structure. If the system looks clever – an ability to synthesize complex reasoning problems – it’s probably fragile. Barbara Liskov observed, “It’s one of the really difficult things about computer science – it’s all about getting the details right.” The Agentic Proposing method’s emphasis on iterative refinement and logical validity reflects this sentiment; achieving true intelligence isn’t merely about assembling impressive components, but ensuring their harmonious interaction and meticulous construction. The multi-granularity policy optimization further reinforces this holistic view, recognizing that effective reasoning demands attention to detail at every level.

Where Do We Go From Here?

The pursuit of robust reasoning in large language models often fixates on scaling parameters or refining architectures. This work suggests a different, and perhaps more fundamental, challenge: the quality of the problems these systems attempt to solve. Agentic Proposing offers a method for constructing increasingly complex problems, but the boundaries of this approach will inevitably reveal themselves. Systems break along invisible boundaries – if one cannot see them, pain is coming. The current framework excels at synthesizing logical problems; extending this to domains requiring common sense, physical intuition, or nuanced social understanding will demand careful consideration of how these skills decompose-and whether they can be meaningfully recomposed.

A key limitation lies in the inherent difficulty of evaluating the ‘difficulty’ of a generated problem. The metrics employed are proxies, at best. Future work must grapple with developing more intrinsic measures of problem complexity, ones that move beyond simple validation scores and consider the cognitive demands placed on a reasoning agent. Anticipating weaknesses requires understanding not just what a model can solve, but how it fails – and constructing problems designed to expose those failures.

Ultimately, the success of this approach, or any like it, will hinge on recognizing that intelligence isn’t simply about finding the right answer, but about gracefully navigating the space of possible questions. A truly robust system will not merely solve problems; it will understand why certain problems are difficult, and construct new ones to push the boundaries of its own understanding.

Original article: https://arxiv.org/pdf/2602.03279.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/