Borrowing Physics to Boost Ecological AI

by

Author: Denis Avetisyan

A novel approach transfers mathematical structures from physics to create more efficient and transferable neural networks for ecological modeling.

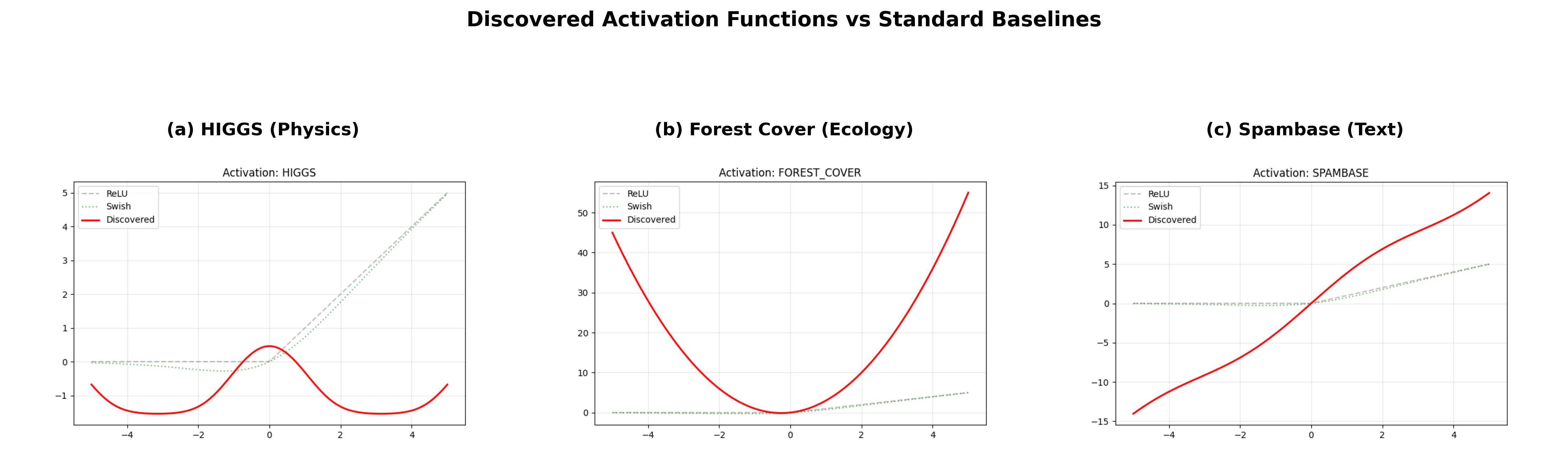
Novel activation functions-including HIGGS with its oscillatory pattern mirroring kinematic periodicity, Forest Cover exhibiting smooth wave-like behavior, and Spambase displaying linear growth modulated by periodicities-demonstrate non-monotonic properties absent in the ReLU function, suggesting an expanded capacity for modeling complex relationships within neural networks.
Novel activation functions-including HIGGS with its oscillatory pattern mirroring kinematic periodicity, Forest Cover exhibiting smooth wave-like behavior, and Spambase displaying linear growth modulated by periodicities-demonstrate non-monotonic properties absent in the ReLU function, suggesting an expanded capacity for modeling complex relationships within neural networks.

This work demonstrates that neuro-symbolic activation discovery, using genetic programming, enables knowledge transfer and parameter efficiency in scientific machine learning applications.

Modern neural networks often employ generic activation functions, overlooking the rich mathematical structure inherent in scientific data-a limitation addressed by ‘Neuro-Symbolic Activation Discovery: Transferring Mathematical Structures from Physics to Ecology for Parameter-Efficient Neural Networks’. This work demonstrates that automatically discovering and applying domain-specific activation functions-derived via genetic programming-can dramatically improve model efficiency and accuracy, revealing a surprising ‘geometric transfer’ phenomenon between fields like physics and ecology. Specifically, activation functions learned from particle physics successfully generalize to ecological classification, achieving comparable accuracy with significantly fewer parameters than conventional networks. Could this approach unlock domain-specific activation libraries, paving the way for a new era of efficient and interpretable scientific machine learning?

The Limits of Conventional Activation Functions: A Systemic Bottleneck

Despite their prevalence in modern neural networks, established activation functions like Rectified Linear Unit (ReLU) and Gaussian Error Linear Unit (GELU) exhibit limitations when confronted with the intricacies of varied datasets. These functions, while computationally efficient, often struggle to model non-linear relationships beyond relatively simple patterns. This inflexibility arises from their fixed shapes and limited capacity to adapt to the specific characteristics of the data they process. Consequently, networks relying heavily on these activations may require a larger number of parameters to achieve comparable performance on complex tasks, hindering their ability to generalize effectively across different domains or to learn efficiently from limited data. The rigid nature of these functions can create bottlenecks, preventing the network from fully capturing the underlying structure and dependencies within the data, ultimately impacting its overall representational power.

A significant challenge in deep learning arises when models trained on one dataset struggle to generalize to another – a phenomenon directly linked to the limitations of standard activation functions. These functions, while effective within a specific domain, often fail to adequately represent the nuanced relationships present in new, unseen data, hindering a process known as transfer learning. This inflexibility necessitates larger models with more parameters to compensate, effectively diminishing parameter efficiency – the ability to achieve high performance with fewer trainable variables. Consequently, the reliance on conventional activation functions can lead to increased computational costs and memory requirements, particularly when adapting models to diverse or evolving datasets, and underscores the need for more expressive alternatives capable of capturing complex feature interactions across domains.

The pursuit of novel activation functions represents a critical frontier in neural network design, as current standards often impose limitations on a model’s capacity to generalize and adapt. Conventional functions, while computationally efficient, may struggle to adequately represent the intricacies present in real-world data, hindering performance on complex tasks and impeding transfer learning capabilities. More expressive activations aim to overcome these bottlenecks by providing the network with a richer set of tools for feature transformation, enabling it to learn more nuanced representations and ultimately construct more robust and adaptable architectures capable of excelling across diverse datasets and problem domains. This ongoing investigation into alternative activation mechanisms is not merely a refinement of existing techniques, but a fundamental step toward unlocking the full potential of deep learning.

Model accuracy generally increases with size, but hybrid models demonstrate nuanced performance, with transfer learning excelling in continuous data domains like forest cover and specialist models succeeding with domain-specific patterns such as those in the Spambase dataset.
Model accuracy generally increases with size, but hybrid models demonstrate nuanced performance, with transfer learning excelling in continuous data domains like forest cover and specialist models succeeding with domain-specific patterns such as those in the Spambase dataset.

Neuro-Symbolic Activation Discovery: Evolving Functionality

The Neuro-Symbolic Activation Discovery framework utilizes Genetic Programming (GP) to automatically generate custom activation functions tailored to specific problem domains. GP operates by creating a population of symbolic expressions – representing potential activation functions – and evolving them through selection, crossover, and mutation. Each expression is evaluated based on its performance when integrated into a neural network and trained on the target dataset. This process iteratively refines the population, favoring expressions that yield improved network accuracy and generalization. The resulting activation functions are not predefined but are instead evolved solutions, offering the potential to surpass the performance of hand-crafted or commonly used activation functions like ReLU or sigmoid. The framework outputs a symbolic representation of the evolved activation function, allowing for direct inspection and understanding of the learned behavior.

The integration of neural networks and symbolic expressions within this framework capitalizes on the strengths of both paradigms. Neural networks excel at learning complex, non-linear relationships from data, but often lack transparency in their decision-making process. Symbolic expressions, conversely, are inherently interpretable and allow for explicit representation of domain knowledge. By combining these, the approach allows for the automation of feature engineering and model construction via Genetic Programming, resulting in models that benefit from both learned representations and explicit, human-understandable rules. This hybridization enables the creation of activation functions that are not simply learned parameters, but are instead compositional expressions built from defined operators and terminal symbols, facilitating analysis and potential generalization beyond the training data.

Automated design of activation functions addresses limitations in both hand-crafted and fully-learned approaches. Traditional activation functions, while computationally efficient, may not optimally suit specific datasets or tasks. Conversely, while neural networks can learn complex mappings, directly learning activation functions within the network parameters can lead to overfitting and reduced generalization. By employing techniques like Genetic Programming to evolve activation functions, the framework seeks to discover functions that enhance feature discrimination and improve model performance on unseen data. This process optimizes for both accuracy and the ability to generalize beyond the training set, potentially yielding models with improved robustness and transfer learning capabilities. The resulting functions are explicitly defined symbolic expressions, enabling analysis and potential reuse across different network architectures and datasets.

A Hybrid Architecture: Demonstrating Performance Gains

Empirical results indicate that a hybrid neural network architecture, utilizing the newly developed activation functions, exhibits consistent performance gains when contrasted with models employing standard activation functions. These gains were observed across multiple experimental runs and datasets, demonstrating the robustness of the approach. The hybrid architecture’s ability to consistently outperform conventional models establishes its efficacy as an alternative to traditional network designs, providing a reliable pathway for improved model performance in various machine learning tasks. Further analysis details the specific performance metrics achieved on each dataset used for validation.

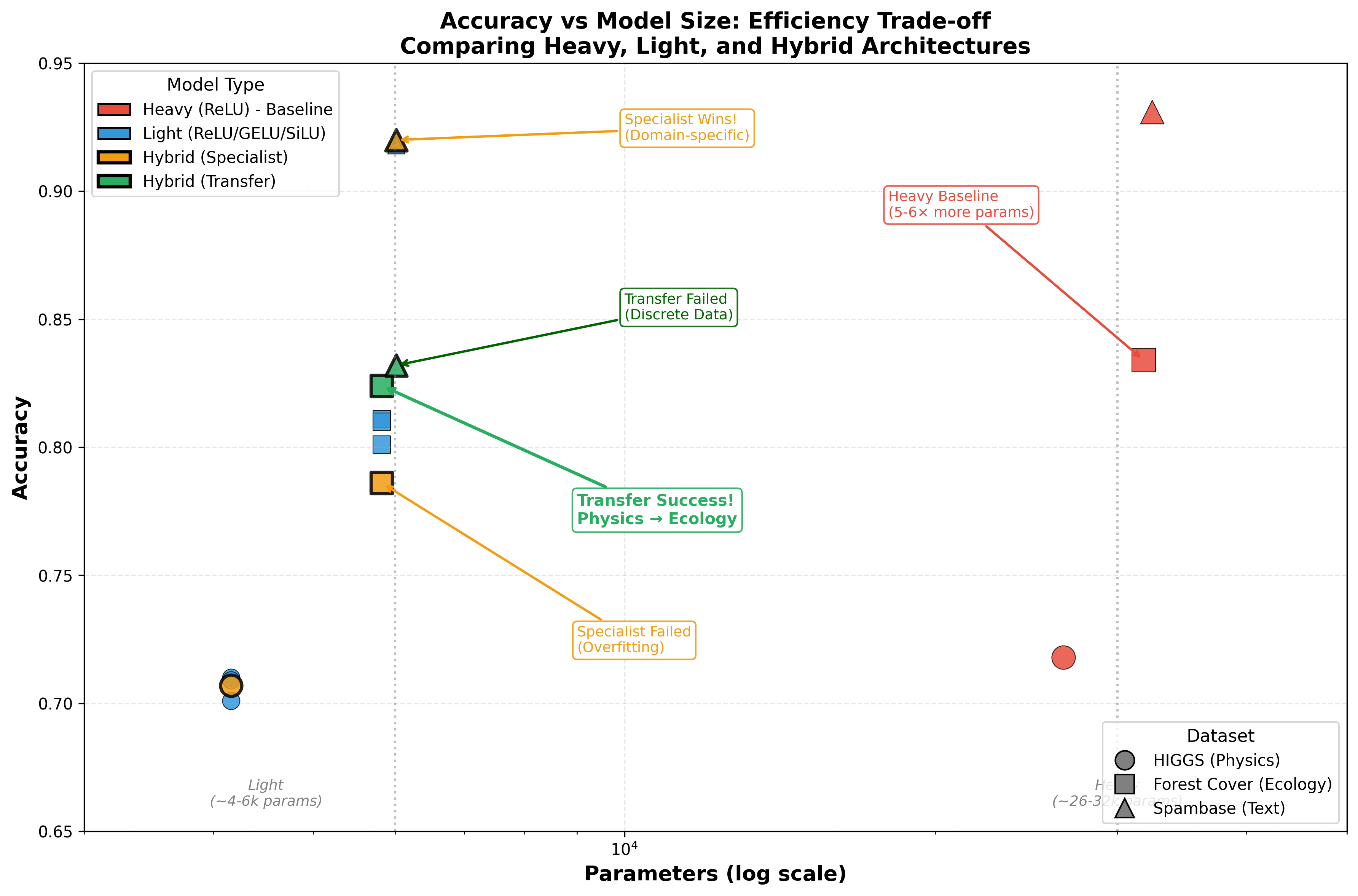
Evaluations demonstrate that the proposed architecture achieves substantial gains in parameter efficiency relative to conventional, heavily parameterized neural networks. Specifically, observed results indicate an 18-21% improvement in parameter efficiency, meaning the model extracts more performance per parameter. This translates to a 5-6× reduction in the total number of parameters required to achieve comparable or superior performance. This reduction is particularly significant as it lowers computational costs associated with both training and inference, and facilitates deployment on resource-constrained devices.

Model validation was performed using three distinct datasets to assess generalizability. The Particle Physics Data, sourced from simulations of high-energy particle collisions, provided a complex, high-dimensional feature space for evaluating performance in a physics-based context. The Forest Cover Data, a multi-class classification problem involving satellite imagery, tested the architecture’s ability to discern subtle patterns in image data. Finally, the Spambase Data, a binary classification dataset consisting of features derived from email characteristics, served to evaluate performance on a common data science benchmark. Performance across these datasets demonstrates the robustness of the hybrid architecture beyond specific data characteristics.

When evaluated on the Forest Cover dataset using a transfer learning methodology, the hybrid architecture attained an accuracy of 82.4%. This performance surpasses that of models utilizing ReLU (81.1%) and GELU (81.0%) activation functions. Notably, this accuracy was achieved while maintaining a parameter count 5.5 times lower than a heavier model which reached 83.4% accuracy on the same dataset. This demonstrates a substantial reduction in model complexity without significant performance degradation.

Batch Normalization was integrated into the hybrid architecture to address internal covariate shift and accelerate the training process. This technique normalizes the activations of each layer, resulting in a more stable learning dynamic and allowing for higher learning rates. Experimental results demonstrate that the inclusion of Batch Normalization consistently improves the performance of the hybrid architecture across all tested datasets. Specifically, it mitigates the vanishing/exploding gradient problem, enabling more effective training of deeper networks and contributing to the observed gains in both accuracy and parameter efficiency compared to models without normalization.

The Geometric Transfer Phenomenon: A New Systemic Understanding

Investigations reveal a compelling ‘Geometric Transfer Phenomenon’ wherein activation functions, refined through evolutionary algorithms on a single continuous dataset, exhibit surprising efficacy when applied to entirely different, yet structurally similar, continuous domains. This suggests that the landscape of optimal activation functions isn’t randomly distributed, but rather possesses an underlying geometric organization – a hidden structure that allows solutions discovered in one area to generalize effectively to others. The observed transferability isn’t simply about memorizing dataset specifics; instead, the evolved functions appear to capture fundamental properties of continuous data, allowing them to perform well across a broader range of tasks than previously assumed. This challenges the traditional paradigm of painstakingly hand-tuning or dataset-specific activation functions and points toward the existence of universal building blocks for neural network design.

Conventional neural network design historically prioritizes the meticulous tailoring of activation functions to the nuances of each individual dataset, a process often requiring extensive experimentation and computational resources. However, recent findings suggest this practice may be unnecessarily restrictive. The observed ability of activation functions – evolved on one continuous dataset – to generalize effectively across diverse continuous domains indicates an underlying geometric structure governs their successful operation. This challenges the long-held belief that optimal performance necessitates dataset-specific activation functions, proposing instead that certain geometrically-informed functions possess an inherent adaptability. Consequently, the focus may shift from bespoke design to identifying and leveraging these broadly applicable functions, potentially streamlining the development of neural networks and enhancing their capacity for transfer learning.

The demonstrated success of geometrically transferable activation functions suggests a paradigm shift in neural network design, paving the way for automated approaches to activation function creation. Rather than relying on manually tuned or randomly initialized functions, future research can focus on algorithms that evolve activation functions optimized for underlying data geometry, potentially yielding architectures with enhanced generalization capabilities and reduced computational cost. This automated design process promises to move beyond the limitations of current, dataset-specific activation functions, fostering the development of neural networks that are inherently more efficient and adaptable to a wider range of complex tasks and datasets – ultimately streamlining the creation of intelligent systems.

Investigations thus far have demonstrated the geometric transfer phenomenon within the confines of shallow neural networks, but extending these principles to deeper architectures represents a crucial next step. The potential benefits of applying this automated activation function design approach to more complex networks are significant; deeper networks, while capable of modeling highly intricate relationships, often suffer from vanishing or exploding gradients and require extensive hyperparameter tuning. Leveraging geometrically informed activation functions could mitigate these challenges, fostering more stable training dynamics and improved generalization performance. Future research will concentrate on whether the transferability observed in shallower models persists when scaling to increased depth, and if modifications to the function design process are needed to accommodate the increased complexity inherent in deeper neural networks. This exploration may reveal fundamental properties of neural network learning and pave the way for the development of truly adaptable and efficient deep learning systems.

The pursuit of parameter efficiency, as detailed in the study, echoes a fundamental principle of elegant system design. This work highlights how transferring mathematical structures – in this case, activation functions – between disciplines like physics and ecology isn’t merely an exercise in applied mathematics, but a recognition of underlying unity. As Donald Davies observed, “Every simplification has a cost, every clever trick has risks.” The Genetic Programming approach, while innovative, demands careful consideration of these trade-offs; a seemingly efficient activation function borrowed from one domain may introduce unforeseen complexities in another. The success of this method hinges on understanding the holistic implications of each transferred component, reinforcing the idea that structure inherently dictates behavior within a system.

Beyond the Activation: Charting Future Directions

The successful geometric transfer of activation functions, as demonstrated, hints at a deeper principle than mere parameter efficiency. It suggests that the scaffolding upon which a model is built – its inherent symmetries and constraints – may be far more critical than the sheer number of parameters. The current work focuses on activation functions, but the methodology could be extended to other architectural components, potentially revealing a universal language of structure applicable across diverse scientific domains. However, this approach is not without its limitations; the reliance on Genetic Programming introduces computational expense, and the transferability of discovered functions remains empirically driven, lacking a robust theoretical underpinning.

A crucial next step lies in developing a more formal understanding of why certain mathematical structures resonate across disciplines. Is there a common thread linking ecological dynamics and physical systems at a fundamental level, or is this simply a case of mathematical isomorphism? Addressing this question requires moving beyond the purely inductive approach of Genetic Programming and incorporating more deductive reasoning, perhaps through the application of category theory or information geometry.

Ultimately, the goal is not merely to create more efficient neural networks, but to build models that reflect the underlying organizational principles of the systems they represent. The current work offers a tantalizing glimpse of this possibility, but the path forward demands a willingness to embrace simplicity, question assumptions, and recognize that the true elegance of a system lies not in its complexity, but in the clarity of its structure.

Original article: https://arxiv.org/pdf/2601.10740.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-01-19 11:02