Beyond the Equation: Guiding Symbolic Regression with Scientific Insight

by

Author: Denis Avetisyan

A new framework addresses the challenge of spurious correlations in equation discovery, ensuring that derived formulas align with established scientific principles.

Quantitative results demonstrate the varying success of different approaches in generating equations, with certain methods failing to produce any output at all.
Quantitative results demonstrate the varying success of different approaches in generating equations, with certain methods failing to produce any output at all.

This work introduces Prior-Guided Symbolic Regression (PG-SR) to mitigate the ‘Pseudo-Equation Trap’ and enhance the scientific consistency of automatically discovered equations using prior constraints and a novel evaluation strategy.

Despite the promise of data-driven discovery, symbolic regression often yields equations that merely fit observational data without reflecting underlying scientific principles-a phenomenon known as the Pseudo-Equation Trap. This paper introduces ‘Prior-Guided Symbolic Regression: Towards Scientific Consistency in Equation Discovery’, a novel framework, PG-SR, that explicitly incorporates domain knowledge as executable constraints to guide the search for scientifically plausible equations. By employing a Prior Annealing Constrained Evaluation mechanism and demonstrating reduced Rademacher complexity, PG-SR demonstrably mitigates the risk of generating spurious relationships. Could this approach unlock a new era of reliable and interpretable equation discovery across diverse scientific disciplines?

The Illusion of Replication: The Limits of Pure Data

Traditional Symbolic Regression (SR) operates by seeking mathematical expressions that best describe a given dataset, a process fundamentally driven by Empirical Risk Minimization. This technique prioritizes minimizing the error between the predicted values of an equation and the observed data points – effectively, finding the curve that fits closest. While seemingly straightforward, this approach can be overly focused on replication rather than revelation. The algorithm isn’t inherently concerned with why a relationship exists, only that it appears to exist within the training data. Consequently, SR often explores a vast space of possible equations, favoring those that achieve a low error rate on the provided examples, regardless of whether those equations reflect underlying physical principles or possess any predictive power beyond the immediate dataset. The success of the regression is thus measured by its ability to mimic the data, potentially overlooking more parsimonious or scientifically meaningful relationships.

The pursuit of equations directly from data, while seemingly objective, can inadvertently lead to the ‘Pseudo-Equation Trap’. This occurs when algorithms prioritize fitting the observed data with minimal error, resulting in equations that perfectly describe the training set but fail to accurately predict new, unseen data. These equations, though mathematically sound for the specific data used, often lack any grounding in established scientific principles and represent spurious correlations rather than genuine causal relationships. Essentially, the algorithm excels at memorization, not understanding, and generates a formula that is contextually accurate but universally meaningless – a mathematical illusion that appears insightful but lacks predictive power beyond the initial dataset. The danger lies in mistaking this perfect fit as evidence of a fundamental law, leading to potentially flawed conclusions and unreliable extrapolations.

Symbolic Regression, while powerful in discerning mathematical relationships from data, is susceptible to identifying connections that are statistically significant but scientifically meaningless without the guiding influence of pre-existing knowledge. The process can readily uncover correlations – patterns where variables change together – that arise purely by chance, particularly when dealing with limited datasets or noisy measurements. These spurious relationships, though accurately reflecting the observed data, do not represent underlying physical laws or causal mechanisms. Consequently, a derived equation – even one with a perfect fit to the training data – may fail spectacularly when applied to new, unseen circumstances. The absence of constraints based on established scientific principles allows the algorithm to prioritize data fitting over the discovery of genuinely generalizable and physically plausible models, highlighting the crucial need to integrate domain expertise into the symbolic regression workflow.

Noisy training data can lead to the acceptance of an incorrect model ([latex]orange[/latex]) that perfectly fits the noise, while simultaneously rejecting a correct model ([latex]blue[/latex]) due to its poor fit to the noise.
Noisy training data can lead to the acceptance of an incorrect model ([latex]orange[/latex]) that perfectly fits the noise, while simultaneously rejecting a correct model ([latex]blue[/latex]) due to its poor fit to the noise.

Guiding the Search: Prior-Knowledge in Equation Discovery

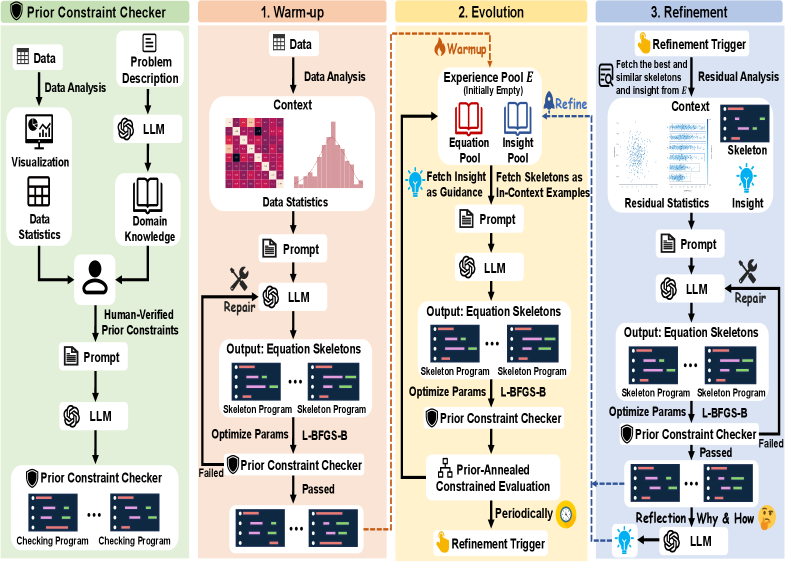
Prior-Guided Symbolic Regression (PG-SR) mitigates the Pseudo-Equation Trap – a common issue in traditional symbolic regression where algorithms generate equations that appear to fit data but lack physical meaning – by directly integrating Prior Constraints. These constraints are derived from existing domain knowledge and represent established scientific principles, physical laws, or expected relationships between variables. By enforcing these constraints during the equation search process, PG-SR biases the algorithm towards solutions that are not only accurate in fitting the provided data, but also consistent with known scientific understanding, thereby reducing the likelihood of generating spurious or physically implausible equations. This approach fundamentally differs from standard symbolic regression, which operates without such prior knowledge and is therefore susceptible to overfitting and the generation of meaningless results.

Prior constraints in PG-SR function as formalized rules that limit the solution space during symbolic regression, thereby directing the search towards physically plausible equations. These constraints are derived from established scientific principles – such as dimensional analysis, conservation laws, or known relationships between variables – and are implemented as penalties within the fitness function. Equations violating these constraints receive lower scores, effectively reducing their probability of being selected during evolutionary processes. This mechanism prevents the discovery of solutions that, while mathematically valid, are physically meaningless or inconsistent with established knowledge, addressing the issue of spurious correlations and improving the reliability of the discovered models. The constraints can take various forms, including functional form restrictions (e.g., requiring a linear relationship), parameter value ranges, or specific relationships between variables, and are crucial for navigating complex search spaces and identifying meaningful scientific relationships.

The Warm-up Stage of Prior-Guided Symbolic Regression (PG-SR) utilizes Large Language Models (LLMs) to generate initial equation structures and corresponding constraints prior to the core symbolic regression process. This stage doesn’t attempt to solve for equation parameters but instead proposes plausible functional forms – or ‘skeletons’ – based on the input data’s description and any provided contextual information. The LLM outputs both the equation’s general form, such as [latex]y = a*x + b[/latex], and a set of constraints defining acceptable parameter ranges, variable relationships, or expected behaviors. These initial proposals significantly reduce the search space for the subsequent symbolic regression algorithm, accelerating convergence and improving the likelihood of discovering meaningful equations.

The Experience Pool is a central repository within the PG-SR framework designed to store and manage candidate equations generated throughout the symbolic regression process. This pool isn’t merely archival; it facilitates iterative refinement by allowing the system to learn from previously evaluated equations. Each equation, along with its associated fitness score and the constraints used in its generation, is stored. Subsequent iterations can then leverage this accumulated knowledge by building upon existing equations, modifying successful components, or avoiding previously unsuccessful approaches, thereby accelerating convergence and improving the quality of discovered equations. The pool’s contents are dynamically updated as new equations are proposed and evaluated, ensuring continuous knowledge accumulation and enabling the system to explore the solution space more efficiently.

The proposed PG-SR framework utilizes a three-stage pipeline-Warm-up, Evolution, and Refinement-to construct a prior constraint checker and improve policy performance.
The proposed PG-SR framework utilizes a three-stage pipeline-Warm-up, Evolution, and Refinement-to construct a prior constraint checker and improve policy performance.

Enforcing Consistency: Mechanisms Within PG-SR

The Prior Constraint Checker functions as a gatekeeper during equation discovery within the PG-SR framework. It systematically evaluates each candidate equation against a pre-defined set of Prior Constraints, which represent established scientific principles and known physical limitations. This validation process involves assessing the equation’s dimensional consistency, ensuring adherence to conservation laws, and verifying that predicted values fall within physically plausible ranges. Equations failing to satisfy all specified Prior Constraints are immediately rejected, preventing the propagation of invalid or non-physical relationships and significantly reducing the search space for scientifically meaningful equations. This rigorous filtering is performed prior to any statistical evaluation, ensuring that only potentially valid equations are considered for further analysis.

The PACE (Progressive Adaptive Constraint Enforcement) Mechanism within PG-SR operates by modulating the stringency of prior constraints during the equation discovery process. Initially, PACE permits a degree of flexibility in satisfying constraints to encourage exploration of the search space. As the search progresses, PACE progressively increases the weight assigned to these constraints, effectively tightening the criteria for accepting candidate equations. This dynamic adjustment is governed by a scheduling function that balances exploration and exploitation; early in the search, the function prioritizes broader exploration, while later stages emphasize refinement within scientifically plausible regions. The mechanism does not simply apply a binary acceptance/rejection rule, but rather uses a weighted scoring system where violations of prior constraints incur penalties that increase over time, thereby steering the search towards solutions aligned with established scientific principles.

PG-SR minimizes the generation of Pseudo-Equations – mathematically valid but physically meaningless expressions – through a dual mechanism of constraint checking and adaptive steering. The Prior Constraint Checker operates as a hard filter, immediately rejecting any candidate equation that violates pre-defined physical laws or established principles. Simultaneously, the PACE mechanism dynamically adjusts the stringency of these constraints during the search process. This adaptive approach allows for initial exploration of a broader equation space while progressively focusing the search on regions likely to yield scientifically consistent results, effectively reducing the probability of converging on Pseudo-Equations and improving the overall reliability of discovered relationships.

Rademacher Complexity, a measure of a function class’s ability to fit random noise, provides a theoretical upper bound on the generalization error of PG-SR. Our analysis quantifies this complexity for the equation discovery process, demonstrating a reduction in Rademacher Complexity achieved through the Prior Constraint Checker and PACE Mechanism. Specifically, the enforcement of Prior Constraints limits the function class considered, thereby decreasing the model’s capacity to overfit to noisy data. Furthermore, the adaptive adjustment of constraint enforcement via PACE contributes to a more efficient search, further minimizing the observed Rademacher Complexity and improving the ability of PG-SR to generalize to unseen data. This reduction in complexity provides a formal justification for the observed performance gains and robustness of the algorithm.

Beyond Approximation: Implications and Future Directions

Progressive Grammar-guided Symbolic Regression (PG-SR) addresses critical shortcomings present in conventional symbolic regression and Transformer-based methods, particularly when tackling complex scientific problems demanding the incorporation of established knowledge. Traditional approaches often struggle with the vastness of the search space, yielding solutions that, while mathematically correct, lack physical plausibility or scientific meaning. PG-SR mitigates this by strategically integrating domain-specific constraints and prior knowledge into the equation discovery process, effectively pruning the search space and guiding the algorithm towards more interpretable and scientifically valid models. This progressive refinement, starting with broad grammatical structures and iteratively adding complexity, allows the system to discover equations that not only fit the data but also align with established scientific principles, offering a powerful advantage in fields where understanding the underlying mechanisms is paramount.

The pursuit of mathematical models from data often yields equations that, while predictive, lack meaningful insight or conflict with established scientific principles. This research demonstrates a pathway toward generating equations that are not merely accurate approximations of observed phenomena, but also inherently interpretable and scientifically sound. By prioritizing solutions aligned with known physical laws and mathematical constraints, the methodology avoids the “black box” problem common in many machine learning techniques. This focus on transparency allows for deeper understanding and validation of the discovered relationships, fostering trust in the resulting models and enabling their effective use in scientific inquiry – for example, ensuring derived [latex]E=mc^2[/latex] is not only a correct prediction but a physically meaningful expression of mass-energy equivalence. The ability to generate equations that are both predictive and understandable represents a significant step forward in the field of symbolic regression, bridging the gap between data-driven discovery and human-comprehensible knowledge.

The synergy between Large Language Model (LLM)-based Symbolic Regression and Program-Guided Symbolic Regression (PG-SR) represents a significant advancement in scientific discovery. LLM-based approaches excel at identifying potential relationships within datasets, leveraging their extensive training to propose plausible equations. However, these models often lack the capacity to enforce scientific constraints or incorporate established domain knowledge. PG-SR addresses this limitation by providing a framework that guides the search process, ensuring that discovered equations adhere to physical laws or other predefined principles. When combined, the data-driven insights of LLMs are intelligently channeled and refined by PG-SR’s knowledge-based guidance, resulting in models that are not only accurate but also interpretable and scientifically valid – a crucial step towards building trust and facilitating deeper understanding in complex systems. This integration effectively bridges the gap between purely data-driven approaches and traditional, knowledge-intensive methods, unlocking the potential for more robust and meaningful scientific insights.

Rigorous experimentation reveals that the proposed Program-Guided Symbolic Regression (PG-SR) consistently surpasses the performance of established symbolic regression techniques and Transformer-based methods across a diverse range of scientific domains. As detailed in Table 1, PG-SR not only achieves greater accuracy in identifying underlying equations governing observed data, but also demonstrates an enhanced capacity to generalize to unseen datasets. This improved performance stems from the strategic integration of prior knowledge, effectively guiding the search process and mitigating the risk of overfitting-a common limitation of purely data-driven approaches. The results highlight PG-SR as a promising advancement in the field, capable of unlocking deeper insights and more reliable models from complex scientific data.

The pursuit of equation discovery, as detailed in the presented framework, benefits from a considered simplicity. The core innovation-Prior-Guided Symbolic Regression-addresses the tendency toward spurious correlations by actively incorporating existing knowledge. This echoes a fundamental principle of effective modeling: reduce noise, amplify signal. As Tim Bern-Lee observed, “The Web is more a social creation than a technical one.” The framework recognizes this inherent interconnectedness of knowledge; prior constraints aren’t limitations, but anchors for consistent, scientifically valid discovery. It’s not about finding an equation, but the equation-the most parsimonious explanation-and clarity is the minimum viable kindness.

What Remains?

The pursuit of equation discovery, even with frameworks like PG-SR, continues to resemble a sculptor chipping away at stone – the true form revealed not by what is added, but by what is definitively removed. The ‘Pseudo-Equation Trap’ is addressed, certainly, but the underlying presumption – that a complex system requires complex description – remains largely unchallenged. A truly successful theory, one anticipates, would necessitate no translation into symbolic form at all. It simply is.

Future work must consider not simply the refinement of prior constraints, but their ultimate obsolescence. Rademacher complexity offers a useful metric, yet it measures the efficiency of approximation, not the elegance of truth. The field fixates on ‘scientific consistency’ as a goal, but consistency is merely the absence of internal contradiction – a low bar. The question is not whether an equation fits the data, but whether the data demands an equation at all.

LLM-guided discovery, while promising, risks amplifying the existing problem – layering sophisticated complexity atop already convoluted systems. Perhaps the most fruitful avenue lies not in finding equations, but in designing experiments that reveal fundamental simplicity. A system that needs instructions has already failed. Clarity, after all, is courtesy.

Original article: https://arxiv.org/pdf/2602.13021.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-16 22:31