Beyond Black Boxes: Uncovering Relationships in Tabular Data

Author: Denis Avetisyan

A new neural network architecture prioritizes interpretability and efficiency by explicitly modeling the mathematical connections between features in structured data.

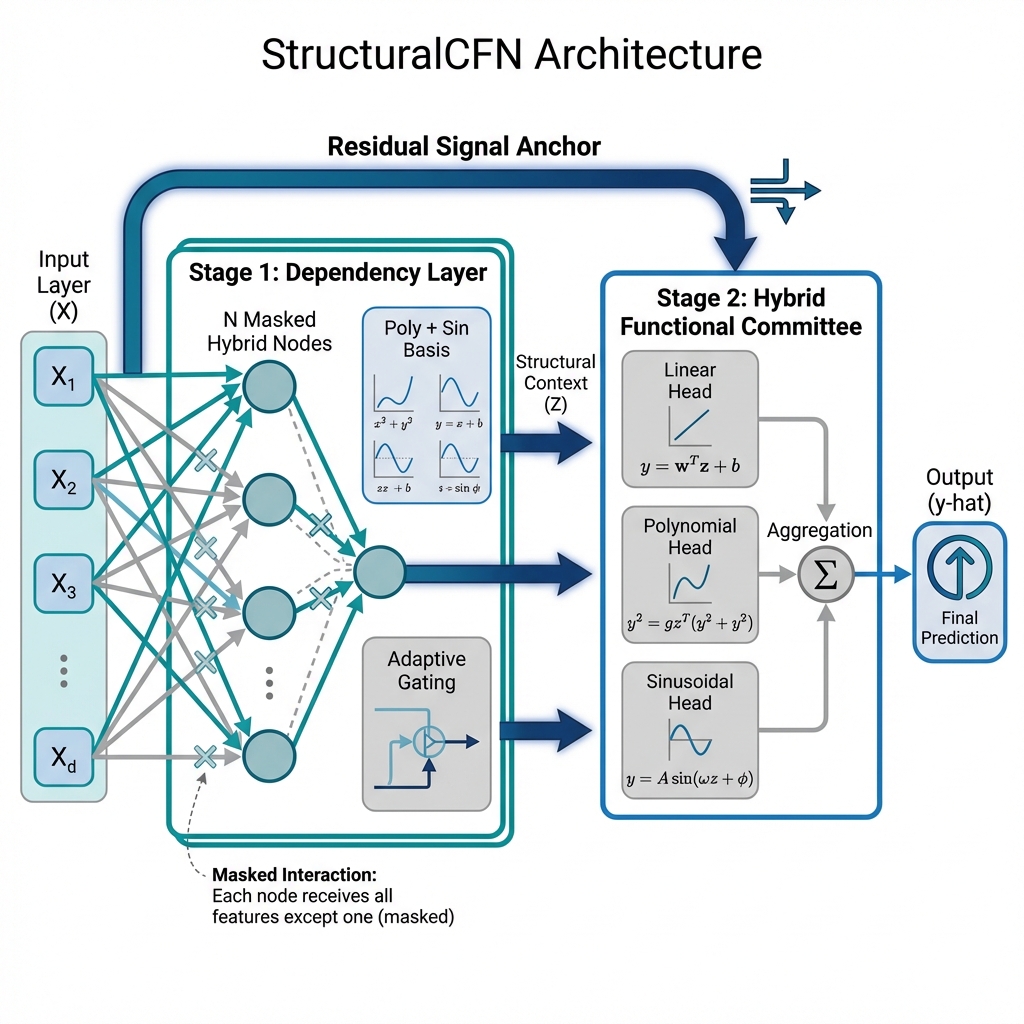
The architecture learns contextual relationships through adaptive gated nodes, ultimately yielding predictions via a hybrid functional committee bolstered by a residual linear bypass-a design prioritizing graceful degradation rather than resisting the inevitable entropy of complex systems.

Structural Compositional Function Networks learn interpretable functional compositions for improved performance and understanding of tabular datasets.

Despite the prevalence of tabular data in critical applications, deep learning models often underperform and lack the interpretability of gradient-boosted trees. This limitation motivates the development of ‘Structural Compositional Function Networks: Interpretable Functional Compositions for Tabular Discovery’, which introduces a novel neural network architecture prioritizing both accuracy and human-understandability. StructuralCFN learns explicit mathematical relationships between features via a structural prior and differentiable adaptive gating, effectively recovering governing data laws as interpretable expressions with a remarkably compact parameter footprint. Could this approach unlock a new paradigm for transparent and efficient machine learning on structured data, bridging the gap between predictive power and scientific insight?

The Evolving Landscape of Predictive Systems

Many machine learning models achieve remarkable predictive accuracy, yet function as largely opaque systems. This lack of transparency-often referred to as the ‘black box’ problem-creates significant challenges for those seeking to understand why a model arrived at a particular decision. While a model might reliably predict outcomes, the inability to trace its reasoning hinders trust, especially in high-stakes applications like healthcare or finance. Debugging becomes considerably more difficult; identifying and correcting errors requires not just observing incorrect outputs, but discerning the internal logic that produced them. Consequently, the power of these models remains limited without the ability to interpret their processes and ensure they are operating on sound, justifiable principles.

The challenge of opaque machine learning models is especially pronounced when analyzing complex tabular datasets. Unlike image or text data where patterns can be intuitively grasped, tabular data-think spreadsheets of medical records, financial transactions, or customer demographics-relies on intricate relationships between features. A model might accurately predict a customer’s likelihood to churn, but without understanding how it arrived at that prediction-which specific features and their interactions drove the result-it’s difficult to trust the model, debug errors, or identify potential biases. These feature interactions-where the effect of one variable depends on the value of another-can be non-linear and subtle, making them difficult for even experienced data scientists to discern from the raw data. Consequently, simply achieving high accuracy isn’t enough; a deep comprehension of these underlying relationships is essential for responsible and effective application of machine learning in domains dealing with complex tabular information.

Growing recognition of the limitations of opaque machine learning models is fueling significant research into explainable AI (XAI) architectures. This isn’t simply a request for post-hoc explanations – attempts to understand a decision after it’s made – but a fundamental shift towards building inherently interpretable systems. Current efforts focus on developing models where the reasoning behind predictions is transparent by design, allowing users to readily identify influential features and understand the logic driving outcomes. This pursuit necessitates a re-evaluation of traditional performance metrics; increasingly, the ability to balance predictive accuracy with clarity and comprehensibility is considered paramount, particularly in high-stakes domains like healthcare, finance, and criminal justice where trust and accountability are essential. The goal is to move beyond simply knowing what a model predicts, to understanding why, fostering greater confidence and enabling effective debugging and refinement.

The learned dependency matrix for the diabetes dataset reveals that LDL cholesterol ([latex]S_2[/latex]) strongly influences triglycerides ([latex]S_5[/latex]) and glucose ([latex]S_6[/latex]), consistent with established clinical metabolic relationships.

Deconstructing Complexity: A Functional Composition Approach

StructuralCFN diverges from conventional neural networks which primarily rely on dot-product operations for feature combination and prediction. Instead, it employs functional composition – the application of one function to the results of another – as its foundational principle. This approach allows the model to build representations by assembling simpler functions, creating a hierarchical structure that inherently enhances interpretability. Unlike dot-product based networks where learned weights obscure the underlying relationships, StructuralCFN’s modularity enables direct inspection of the composed functions and their individual contributions to the final output. This compositional structure facilitates understanding of how the model arrives at its predictions, offering a significant advantage in applications requiring transparency and explainability.

The Compositional Function Network (CFN) forms the central component of StructuralCFN and operates by representing complex relationships as compositions of simpler, predefined functions known as basis functions. These basis functions include Polynomial Nodes, which generate polynomial terms to capture non-linear interactions, and Periodic Nodes, which produce sinusoidal outputs suitable for modeling cyclical patterns. By combining these and other basis functions through composition – applying one function to the output of another – the CFN constructs a hierarchical representation of the target function. The output of the network is a weighted sum of these composed basis functions, allowing for flexible modeling of both linear and non-linear dependencies within the data.

StructuralCFN achieves universal function approximation by composing basis functions, a principle rooted in the Stone-Weierstrass theorem. This allows the network to represent any continuous function [latex]f: [a, b] \rightarrow \mathbb{R}[/latex] to an arbitrary degree of accuracy. The composition process involves applying these functions sequentially, effectively creating a hierarchical representation of the target function. This compositional structure provides flexibility in modeling complex relationships, as the network can learn to combine simple functions in intricate ways, and expressiveness because the depth and breadth of composition can be adjusted to match the complexity of the data. The resulting network is not limited by the fixed feature spaces inherent in traditional methods, offering a potentially more efficient and accurate representation for a wide range of continuous functions.

Revealing Structure: Dependencies and Prior Knowledge

StructuralCFN incorporates a Dependency Layer to establish a structural prior, operating on the principle that the value of a given feature is not independent but is instead determined by the values of its neighboring features within the data. This approach moves beyond traditional feature independence assumptions common in many machine learning models. The Dependency Layer functions by analyzing the relationships between features during the training process, identifying and quantifying these contextual dependencies. This learned structural prior is then used to inform the model’s predictions, allowing it to leverage the inherent relationships within the data to improve accuracy and generalization performance. Essentially, the model learns how features relate to each other, rather than treating them as isolated variables.

The Context-Gated Structural Prior enables adaptive learning of inter-feature dependencies within StructuralCFN by modulating the influence of neighboring features based on contextual information. This is achieved through a gating mechanism that assigns weights to dependencies, effectively determining the degree to which each feature’s value is informed by its neighbors. The gating function itself is conditioned on the input data, allowing the model to dynamically adjust the strength of these dependencies for each individual instance and feature. This adaptive weighting contrasts with static dependency structures and allows the model to focus on the most relevant relationships within the data, improving performance and generalization capability.

The Dependency Matrix within StructuralCFN serves as a quantifiable representation of inter-feature relationships, explicitly detailing the learned strength of dependency between each feature pair. This matrix, of size [latex]N \times N[/latex] where [latex]N[/latex] is the number of features, contains values representing the degree to which one feature is predicted based on another. Higher values indicate stronger dependencies, facilitating analysis of feature importance and potential redundancies. The matrix enables targeted investigation of specific feature interactions, informing model interpretability and potentially revealing opportunities for feature selection or engineering. This visualization allows researchers to directly assess the model’s understanding of structural relationships within the data, beyond simply observing predictive performance.

Mapping Manifolds and Promoting Sparsity

The system employs a Differentiable Adaptive Gate, a trainable neural network component, to dynamically identify the underlying manifold structure present within the input data. This gate learns to modulate the flow of information, effectively weighting different features based on their relevance to the intrinsic dimensionality and geometric properties of the data. By automatically discovering these manifold characteristics – as opposed to relying on pre-defined or fixed assumptions – the architecture achieves improved modeling accuracy across diverse datasets. The differentiability of the gate allows for end-to-end training via gradient descent, optimizing the manifold discovery process alongside the overall model parameters. This adaptive approach contrasts with traditional methods requiring explicit dimensionality reduction or feature engineering to account for manifold effects.

L1 regularization, also known as Lasso regression, is implemented to promote model sparsity by adding a penalty proportional to the absolute value of the model’s parameters to the loss function. This encourages the model to drive the weights of less important features to zero, effectively performing feature selection and simplifying the model. The resulting sparse model improves generalization performance by reducing overfitting to the training data and enhancing interpretability, as only a subset of features contribute significantly to the predictions. The strength of this regularization is controlled by a hyperparameter, λ, which determines the magnitude of the penalty.

The Aggregation Layer employs a Hybrid Functional Committee to improve prediction robustness by integrating both linear and non-linear functional heads. This committee structure allows the model to capture a wider range of data relationships; linear heads efficiently model predictable, first-order effects, while non-linear heads address complex interactions and residual variance. The outputs of these functional heads are then combined, weighted by learned parameters, to generate the final prediction, effectively creating an ensemble within the aggregation process and improving generalization performance across diverse datasets. This approach avoids reliance on a single model type and enhances the model’s ability to handle both simple and intricate data patterns.

Towards Accountable and Insightful Artificial Intelligence

A notable step forward in the pursuit of transparent artificial intelligence has been achieved with the development of StructuralCFN, a model designed not only to predict outcomes but to elucidate the reasoning behind those predictions. Unlike many complex ‘black box’ AI systems, StructuralCFN prioritizes interpretability, allowing users to trace the decision-making process and understand how specific input features contribute to a given output. This is accomplished through its unique architecture, which explicitly models the structural dependencies between variables, revealing the underlying relationships that drive its conclusions. Consequently, this capability is crucial in domains where trust and accountability are paramount, as it provides a clear audit trail and facilitates error diagnosis, ultimately fostering greater confidence in AI-driven solutions.

StructuralCFN distinguishes itself through an exceptional efficiency in model size without sacrificing predictive power. While many contemporary, state-of-the-art models, such as the FT-Transformer, rely on millions of parameters to achieve high performance, StructuralCFN accomplishes comparable results with a remarkably streamlined architecture of only approximately 300 parameters. This dramatic reduction in complexity not only minimizes computational demands but also contributes directly to the model’s improved interpretability, offering a pathway to artificial intelligence systems that are both powerful and readily understood – a significant advantage for applications demanding transparency and trust.

Recent evaluations demonstrate that StructuralCFN achieves superior performance on the Diabetes dataset when contrasted with the established LightGBM algorithm. Specifically, StructuralCFN registered a performance score of 0.488, notably outperforming LightGBM’s score of 0.520 – a difference determined to be statistically significant with a p-value less than 0.05. This result indicates that StructuralCFN not only offers enhanced interpretability, but also delivers improved predictive accuracy in the context of diabetes diagnosis or risk assessment, suggesting a potential advancement in clinical decision support tools.

Evaluations across diverse medical datasets demonstrate StructuralCFN’s capacity to deliver enhanced predictive accuracy alongside interpretability. Specifically, when applied to the Breast Cancer and Heart Disease datasets, the model consistently surpassed the performance of LightGBM, a widely used gradient boosting algorithm. Statistical analysis confirms these improvements are significant, with p-values less than 0.05, and resulting in performance values of 0.062 for Breast Cancer detection and 0.440 for Heart Disease prediction; these results suggest StructuralCFN can effectively capture complex relationships within medical data, offering a potentially valuable tool for diagnostic and prognostic applications.

Rigorous testing of StructuralCFN involved generating synthetic datasets governed by known mathematical relationships, and the model demonstrated a remarkable ability to rediscover these underlying rules. Across twenty independent trials, utilizing varied data distributions and relationship complexities, StructuralCFN consistently and accurately recovered the [latex]f(x)[/latex] function defining the synthetic data with 100% accuracy. This achievement highlights the model’s capacity not merely to predict, but to truly understand the relationships within data – a crucial step towards building AI systems that are both reliable and transparent, and capable of generalizing beyond the training set.

The effectiveness of StructuralCFN stems from its inherent capacity to model structural dependencies within data, a capability proving invaluable in contexts demanding comprehension of feature interactions. Unlike many contemporary AI systems treated as ‘black boxes’, this architecture doesn’t simply identify correlations; it actively maps the relationships between variables, revealing how changes in one feature propagate through the system to influence predictions. This is particularly crucial in fields like medical diagnosis, financial modeling, and scientific discovery, where understanding the ‘why’ behind a result is often as important as the prediction itself. By explicitly representing these structural connections, StructuralCFN offers not just accuracy, but also a level of transparency that fosters trust and enables informed decision-making, moving beyond mere prediction to genuine insight.

The development of StructuralCFN represents a crucial step toward realizing truly dependable artificial intelligence. Unlike many high-performing models that operate as ‘black boxes’, this architecture prioritizes both accuracy and transparency; it doesn’t just predict outcomes, but elucidates the reasoning behind them. This combination is achieved with remarkable efficiency – achieving competitive results with a fraction of the parameters required by contemporary models. Through rigorous testing on datasets ranging from medical diagnostics to synthetic data, StructuralCFN consistently demonstrates superior performance and the ability to reveal underlying relationships, fostering trust and enabling informed decision-making in critical applications where understanding feature interactions is paramount. This advance suggests a future where AI isn’t simply powerful, but also accountable and readily understood.

The pursuit of StructuralCFN echoes a fundamental principle of enduring systems; it isn’t simply about achieving a result, but how that result is achieved. This research prioritizes interpretable mathematical relationships within tabular data, recognizing that architecture without history-or, in this case, transparent function-is fragile. As Tim Bern-Lee stated, “The web is more a social creation than a technical one.” This sentiment aligns with StructuralCFN’s focus; it builds upon a structural prior, much like the web’s foundational protocols, to create a system that isn’t merely functional, but understandable and adaptable over time. The architecture’s emphasis on explicit functional composition aims for an elegant decay, allowing for continued learning and refinement rather than abrupt obsolescence.

What Lies Ahead?

The pursuit of interpretable machine learning for tabular data, as exemplified by StructuralCFN, inevitably encounters the limitations inherent in any attempt to impose order on complex systems. The architecture offers a compelling initial step towards explicitly modeling functional relationships, yet it remains to be seen whether this approach scales gracefully with dimensionality and data heterogeneity. The elegance of learned compositions may yield to the brute force of accumulated complexity-technical debt manifesting as increasingly opaque functional graphs.

Future work must address the tension between expressive power and parsimony. Simply achieving high accuracy is a transient phase; the true measure of success will be the capacity to maintain performance while resisting the entropy of overfitting. The field should also consider the broader implications of structural priors: are these merely convenient heuristics, or do they reflect underlying truths about the generative processes of tabular data?

Ultimately, the quest for interpretable models is not about achieving a static state of understanding, but about creating systems that age gracefully-those that reveal, rather than conceal, the inevitable decay of predictive power. Uptime, in this context, is a rare phase of temporal harmony, a momentary reprieve from the relentless march of statistical drift.

Original article: https://arxiv.org/pdf/2601.20037.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/