AI Uncovers Hidden Equations of Nature

Author: Denis Avetisyan

Researchers are leveraging the power of artificial intelligence to automatically discover fundamental equations governing complex physical phenomena.

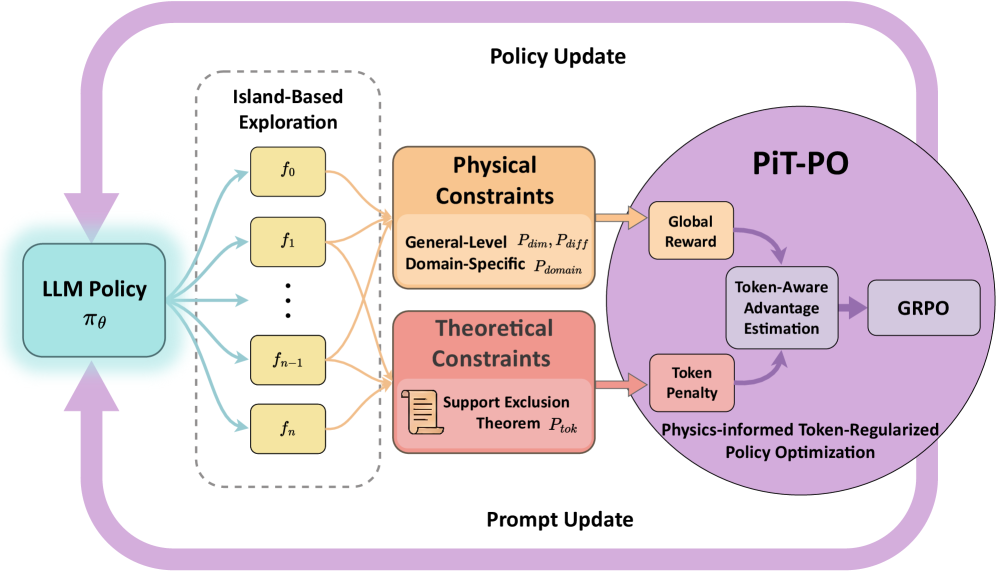
The PiT-PO framework refines large language models into adaptive equation generators through a reinforcement learning process driven by dual-constraint evaluation-balancing physical feasibility with theoretical consistency-to produce parsimonious and physically plausible results at a token level, effectively moving beyond static proposition towards dynamic refinement.

A novel framework, PiT-PO, combines large language models with physics-informed constraints and reinforcement learning for accurate and interpretable symbolic regression, particularly in turbulence modeling.

Despite the promise of large language models (LLMs) for scientific discovery, existing approaches to symbolic regression often treat them as static generators, yielding equations lacking physical consistency or structural parsimony. This work introduces PiT-PO, a novel framework detailed in ‘LLM-Based Scientific Equation Discovery via Physics-Informed Token-Regularized Policy Optimization’, which evolves LLMs into adaptive generators via reinforcement learning and rigorously enforces both hierarchical physical validity and token-level redundancy penalties. Consequently, PiT-PO achieves state-of-the-art performance on standard benchmarks and successfully discovers novel turbulence models, even empowering smaller models to outperform larger, closed-source alternatives. Could this approach democratize access to advanced scientific modeling and accelerate discovery across diverse domains?

The Turbulence Trap: Why Simple Equations Fail

The persistent difficulty in accurately modeling turbulent flow represents a fundamental hurdle across numerous scientific and engineering disciplines. Turbulence, characterized by chaotic and unpredictable fluid motion, impacts everything from the efficiency of aircraft wings and internal combustion engines to the accuracy of weather prediction and climate models. Current computational methods often struggle to resolve the full spectrum of scales inherent in turbulent flows, necessitating the use of approximations and statistical models. This reliance on simplification introduces uncertainties that can significantly limit the predictive power of simulations, hindering progress in fields that depend on reliable fluid dynamics calculations. Addressing this challenge requires not only increased computational power but also innovative theoretical frameworks and modeling techniques capable of capturing the complex interplay of forces governing turbulent behavior.

Conventional approaches to establishing the equations that govern fluid motion frequently stumble when confronted with the chaotic reality of turbulence. These methods typically depend on substantial simplifications of the underlying physics, or the incorporation of data gleaned from specific, limited experiments. While useful in certain controlled conditions, these simplifications introduce inaccuracies when attempting to predict behavior in more complex, real-world scenarios. For instance, assuming a fluid is perfectly uniform or neglecting the interplay between different scales of motion can lead to significant deviations between modeled predictions and actual observations. Consequently, current models often struggle to accurately forecast phenomena like weather patterns, aircraft drag, or the efficiency of energy transfer in turbulent flows, highlighting the need for more robust and fundamentally grounded theoretical frameworks.

The [latex]ReynoldsStressTensor[/latex] occupies a pivotal role in describing turbulent flows, effectively representing the forces exerted by turbulent eddies on the surrounding fluid; however, its accurate determination presents formidable challenges. This tensor isn’t a simple scalar value but a complex mathematical object with six independent components, each reflecting stress in a particular direction. Directly solving for these components within the governing Navier-Stokes equations is computationally prohibitive due to the vast range of scales involved in turbulence – from large, energy-containing eddies to the smallest dissipative structures. Consequently, turbulence models often rely on approximations and closure schemes to represent the [latex]ReynoldsStressTensor[/latex], introducing uncertainties and limitations. Furthermore, physical constraints, such as the requirement for positive definite stress tensors to ensure physically realistic behavior, complicate the development of accurate and stable closure models. Overcoming these mathematical and physical constraints is therefore crucial for improving the predictive capability of turbulence models across a wide range of engineering and environmental applications.

The learned model accurately predicts stream-wise velocity contours, aligning closely with both DNS data and the standard [latex]k-\omega SST[/latex] RANS model.

From Black Boxes to Equations: A Glimmer of Hope

Symbolic regression is a type of regression analysis that seeks to identify a mathematical expression that best describes the relationship between input variables and output variables. Unlike traditional regression which assumes a predefined functional form – such as a linear or polynomial model – symbolic regression operates by searching the space of possible mathematical expressions. This search is typically performed using evolutionary algorithms, which iteratively refine candidate equations based on their ability to fit observed data, measured by a fitness function – often based on minimizing the residual sum of squares. The output of a symbolic regression process is a mathematical equation, expressed in terms of basic mathematical operators [latex]\left( +, -, *, /, \sin, \cos, \exp, \log \right)[/latex], that provides a compact and interpretable model of the underlying data generating process. This differs from black-box models, offering insights into the relationships between variables and potentially revealing underlying physical laws.

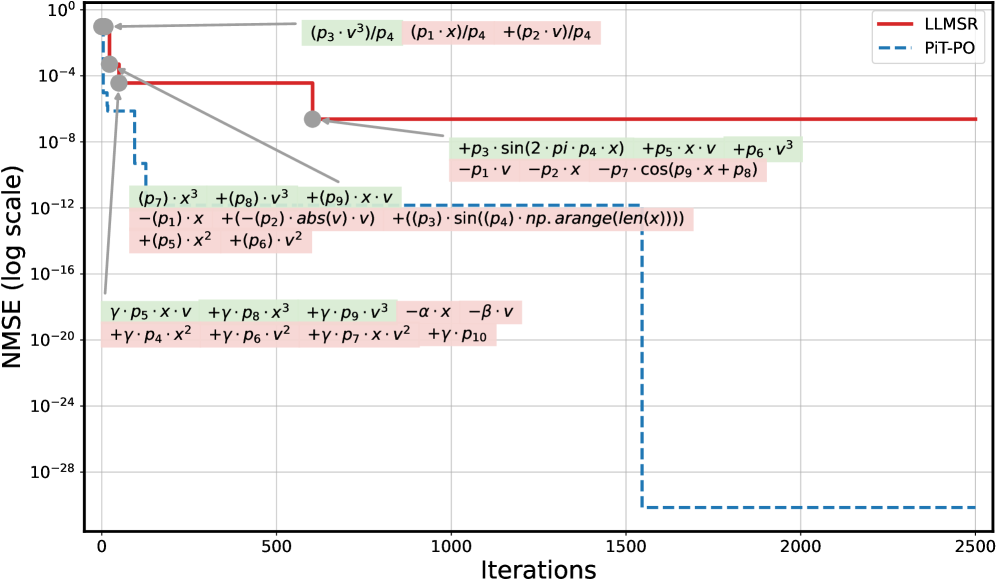
Large Language Models (LLMs) improve symbolic regression (LLM-SR) by introducing a prior probability distribution over potential equation structures. Traditional symbolic regression methods often explore the equation space randomly, leading to inefficient searches. LLM-SR, conversely, utilizes the LLM’s pre-existing knowledge of mathematical relationships and syntax to guide the search toward more plausible equations. This is achieved by prompting the LLM to generate candidate equations, effectively biasing the search space. The LLM assigns higher probabilities to equations that conform to typical mathematical forms and relationships observed during its training, increasing the likelihood of discovering simpler, more generalizable models that fit the provided data. This prior distribution significantly reduces the computational cost and improves the success rate of equation discovery compared to unguided approaches.

Direct application of Large Language Models (LLMs) to symbolic regression faces limitations regarding adherence to physical plausibility and mathematical correctness. While LLMs excel at generating syntactically valid expressions, they lack inherent understanding of physical units or dimensional analysis, often producing equations with inconsistent or meaningless terms. Furthermore, LLMs may struggle to consistently enforce mathematical constraints such as positivity, monotonicity, or boundary conditions, leading to solutions that, while fitting the training data, are not mathematically well-defined or physically realistic. This necessitates the incorporation of additional mechanisms, such as penalty terms or constraint satisfaction modules, to guide the LLM towards generating valid and meaningful equations, or the use of techniques to verify and correct LLM-generated expressions post-hoc.

LLM-SR and PiT-PO ([latex]Llama-3.1-8B[/latex]) consistently reduce Normalized Mean Squared Error (NMSE) across the LLM-SR Suite, as demonstrated by median trajectories (lines) and the range of performance across different seeds (shaded regions), with detailed results for smaller models in Appendix C.1.

PiT-PO: Forcing the LLM to Play by the Rules

PiT-PO utilizes a novel framework to convert Large Language Models (LLMs) into adaptive generators for symbolic regression. This is achieved through the implementation of InSearchPolicyOptimization, a process that dynamically refines the search strategy employed by the LLM during equation discovery. Rather than a static search, the policy is iteratively improved based on the performance of generated equations, guiding the LLM towards more promising areas of the search space. This optimization focuses on balancing exploration – investigating diverse equation forms – with exploitation – refining equations that show initial promise. The resulting adaptive search process significantly enhances the efficiency and accuracy of symbolic regression performed by the LLM, allowing it to discover equations that effectively model the underlying data.

PiT-PO’s core functionality relies on `DualConstraintEvaluation`, a process that assesses candidate equations generated by the LLM against two distinct constraint sets. `MathematicalConstraints` verify the validity of the equation’s structure and operators – ensuring, for example, dimensional consistency and adherence to algebraic rules. Simultaneously, `PhysicalConstraints` validate the equation’s physical plausibility, enforcing adherence to known physical laws governing the modeled system. This concurrent evaluation, rather than sequential filtering, allows for more efficient pruning of invalid candidates and prioritizes solutions that satisfy both mathematical rigor and physical realism, improving the overall accuracy and reliability of the symbolic regression process.

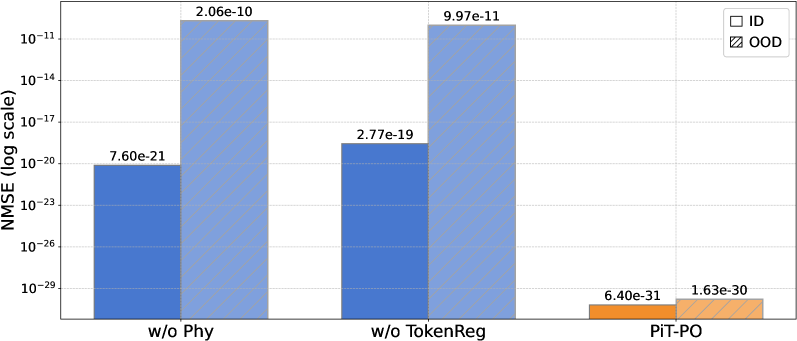
The PiT-PO framework incorporates constraints beyond data fitting to enhance the validity of discovered equations. Specifically, it enforces both mathematical and physical constraints, including [latex]EnergyConsistency[/latex] and [latex]BoundaryConditionConsistency[/latex], alongside a critical [latex]RealizabilityConstraint[/latex] which ensures the derived equations represent physically plausible systems. Evaluation on the LLM-SRBench dataset demonstrates that this constraint-driven approach achieves a symbolic accuracy of up to 94.6%, indicating a substantial improvement in the reliability and correctness of the generated symbolic regressions compared to methods focused solely on data fidelity.

Iterative searches using PiT-PO and LLM-SR on Oscillator1 with Llama-3.1-8B-Instruct progressively refine equation structures, as indicated by decreasing Normalized Mean Squared Error (NMSE) and the evolution from erroneous (red) to correct (green) terms.

Putting PiT-PO to the Test: Turbulent Flows and Beyond

The challenge of turbulence modeling received focused attention through the application of PiT-PO, a novel approach tested rigorously against the well-established benchmark of [latex]PeriodicHillFlow[/latex]. This specific flow configuration, characterized by periodic obstacles generating complex turbulent structures, served as an ideal proving ground for the method. By targeting this computationally demanding scenario, researchers aimed to demonstrate PiT-PO’s capacity to accurately represent the intricate dynamics of turbulent flows, a longstanding problem in fluid dynamics. The selection of [latex]PeriodicHillFlow[/latex] allowed for detailed comparison with existing models and validation against established experimental data, ultimately showcasing PiT-PO’s potential as a powerful tool for advancing turbulence research and engineering applications.

The predictive capability of PiT-PO is demonstrated through its successful discovery of governing equations for turbulent flow, a notoriously complex physical phenomenon. By analyzing data from the Periodic Hill Flow benchmark, PiT-PO autonomously formulated equations that accurately capture the intricate dynamics of turbulence, going beyond simple data fitting. This isn’t merely a replication of known behavior; the discovered equations reveal underlying relationships within the flow, allowing for robust predictions of how the turbulence will evolve under various conditions. The method’s effectiveness lies in its ability to distill the essential physics from data, providing a powerful tool for modeling and understanding fluid dynamics where traditional approaches often fall short. [latex]Re = \frac{U L}{\nu}[/latex]

The predictive capability of the newly discovered equations extends beyond mere alignment with experimental data; they inherently adhere to established physical constraints governing fluid dynamics. This rigorous consistency bolsters confidence in the model’s reliability and generalizability, suggesting an understanding of the underlying physics rather than simply memorizing patterns. Quantitative assessment confirms this qualitative strength, as the equations consistently achieve lower Normalized Mean Squared Error (NMSE) values when benchmarked against Large Language Model-based Subgrid Reynolds stress modeling (LLM-SR). This superior performance indicates a more accurate representation of turbulent flow behavior, offering a promising advancement in turbulence modeling techniques and highlighting the potential for physics-informed machine learning approaches.

Investigations reveal that PiT-PO not only models known turbulent flows with precision but also exhibits a robust capacity to generalize to previously unseen conditions. This is evidenced by its significantly lower Normalized Mean Squared Error out-of-distribution (NMSEOOD) compared to alternative methods. Importantly, PiT-PO achieves this enhanced predictive power within a constrained computational budget – specifically, a fixed allocation of 25,000 seconds – while simultaneously minimizing the Normalized Mean Squared Error (NMSE). This efficiency suggests that PiT-PO offers a compelling balance between accuracy, generalization ability, and computational cost, making it a promising tool for tackling complex fluid dynamics problems where extrapolating to new scenarios is crucial.

Comparison of Reynolds stress components reveals that [latex]RANS[/latex], [latex]DSRRANS[/latex], [latex]LLM-SR[/latex], [latex]PiT-PO[/latex], and [latex]DNS[/latex] exhibit distinct anisotropic behavior in periodic hill training flow.

A Glimmer of Automation in the Pursuit of Knowledge

PiT-PO signifies a considerable advancement in the automation of scientific inquiry, offering researchers a powerful new tool for navigating the intricacies of complex systems. Traditionally, discovering relationships within these systems demanded extensive manual experimentation and analysis; PiT-PO, however, employs algorithms to systematically search for underlying equations governing observed data, drastically reducing the time and resources required. This framework doesn’t simply correlate data points; it actively seeks out physically plausible explanations, leveraging known physical principles to guide its search and ensure the discovered relationships are not merely statistical anomalies. By automating this crucial step in the scientific process, PiT-PO promises to accelerate discovery across diverse fields, allowing scientists to focus on interpreting results and formulating new theories rather than being bogged down in exhaustive data analysis.

PiT-PO distinguishes itself by directly embedding known physical principles into its equation discovery process, a departure from traditional ‘black box’ machine learning approaches. This integration isn’t merely about feeding data into an algorithm; rather, the framework actively constrains the search space to solutions that adhere to fundamental laws – such as conservation of energy or Newton’s laws of motion. Consequently, PiT-PO doesn’t just identify correlations within data; it seeks equations that accurately represent the underlying physics governing a system. This capability is particularly crucial when dealing with limited datasets or noisy data, where purely data-driven methods often struggle. By prioritizing physical plausibility, the framework increases the likelihood of uncovering truly generalizable equations, potentially revealing previously unknown relationships and accelerating the pace of scientific discovery in fields ranging from fluid dynamics to materials science. The system can, for example, search for equations describing the motion of a pendulum, not simply memorizing the observed trajectory, but deriving an equation akin to [latex] \theta”(t) + \frac{g}{L} \sin(\theta(t)) = 0 [/latex], which captures the underlying oscillatory behavior.

Researchers are actively broadening the application of the PiT-PO framework beyond its initial successes, with ongoing efforts targeting diverse scientific fields such as materials science, molecular biology, and even social sciences. This expansion isn’t merely about applying the same algorithms to different data; it involves adapting the system to accommodate the unique governing principles and complexities inherent in each domain. A key area of investigation centers on PiT-PO’s capacity to move beyond equation discovery and begin formulating entirely new, testable hypotheses-essentially, acting as a generative engine for scientific inquiry. The ultimate goal is to leverage the framework’s ability to identify patterns and relationships within data to not only explain existing phenomena but also to predict previously unknown interactions and guide future experimentation, potentially accelerating the pace of discovery across multiple disciplines.

Ablation studies demonstrate that removing components from PiT-PO negatively impacts its performance, highlighting the importance of each constituent part.

The pursuit of elegant solutions, as demonstrated by this PiT-PO framework for scientific equation discovery, often feels like building sandcastles against the tide. The article details a method to guide Large Language Models with physics-informed constraints – a valiant attempt to impose order on chaos. It’s a temporary reprieve, though. One can’t help but recall Edsger W. Dijkstra’s observation: “Program testing can be a very effective process, but it can never be complete.” The tests will pass, the model will seem robust, until production, inevitably, exposes the hidden assumptions and edge cases. The beauty isn’t in the discovered equation, but in how long it delays the inevitable entropy.

What’s Next?

The pursuit of automated equation discovery, predictably, has arrived at a point where the complexity of the scaffolding threatens to eclipse the simplicity of the underlying physics. This ‘PiT-PO’ framework, while demonstrating a capacity for symbolic regression, merely delays the inevitable. The problem isn’t finding an equation that fits the data – that’s been solvable with increasingly elaborate curve-fitting for decades. It’s finding one that generalizes beyond the training domain, and doesn’t collapse into a monstrous overparameterized mess when confronted with actual production data. They’ll call it AI and raise funding, naturally.

The real challenge isn’t the Large Language Model itself, but the encoding of ‘physics-informed constraints’. Right now, it feels… brittle. A meticulously crafted loss function, designed to nudge the model towards acceptable behavior, will inevitably fail in corner cases. The system, once a simple bash script that plotted a line, will become a sprawling, undocumented labyrinth of regularization terms. And, inevitably, the documentation will lie again.

Future work will undoubtedly focus on scaling – larger models, more data, even more constraints. But a more fruitful avenue might involve accepting imperfection. Perhaps the goal shouldn’t be discovering the ‘true’ equation, but generating a family of approximations, each valid within a specific regime. Acknowledging the inherent limitations of the model, and building in mechanisms for graceful degradation, might be a more realistic-and ultimately more useful-path forward. Tech debt is just emotional debt with commits, after all.

Original article: https://arxiv.org/pdf/2602.10576.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/