AI-Powered Physics: Scaling Assessment with Generated Problems

Author: Denis Avetisyan

Researchers have developed a system leveraging artificial intelligence to automatically create and verify large numbers of physics problems, paving the way for more robust and scalable educational assessments.

The distribution of student accuracy on problem bank 6-1 closely mirrors that of a language model simulation, with error bars quantifying the inherent measurement uncertainty in both assessments.

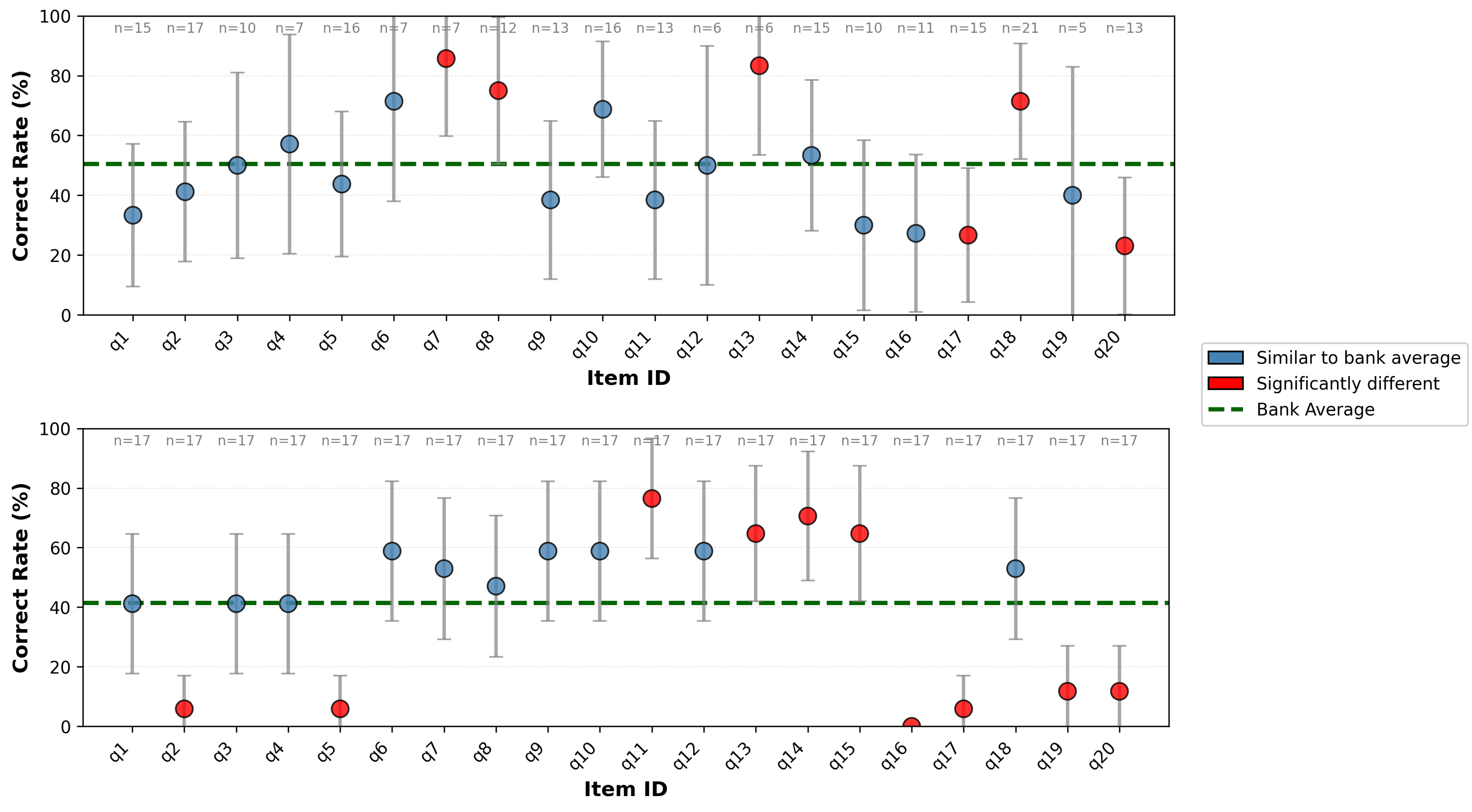
This work details a framework using large language models and prompt chaining to generate and validate isomorphic physics problems for reliable, large-scale assessment.

Traditional STEM assessment methods struggle with accessibility, security, and comparability at scale. This paper introduces a framework-‘Scalable Generation and Validation of Isomorphic Physics Problems with GenAI’-leveraging large language models to automatically generate and rigorously validate large banks of isomorphic physics problems. Results demonstrate that this approach yields assessment banks with statistically homogeneous difficulty, as corroborated by strong correlations (Pearson’s ρ up to 0.594) between language model evaluations and actual student performance. Could this framework offer a pathway toward more robust, adaptable, and equitable educational assessment systems?

The Illusion of Mastery: Why We Teach Procedures, Not Physics

Physics instruction frequently prioritizes the application of formulas to solve a high volume of standardized problems, a practice that inadvertently fosters memorization over genuine comprehension. This emphasis on repetitive problem-solving often trains students to recognize patterns and apply pre-learned solutions, rather than encouraging them to develop a deep understanding of underlying physical principles. Consequently, learners may excel at replicating solutions to familiar problems but struggle when confronted with novel scenarios requiring conceptual application and critical thinking. The approach inadvertently shifts the focus from understanding [latex]F = ma[/latex] to simply applying it, hindering the development of transferable problem-solving skills essential for future scientific endeavors and a robust grasp of physics itself.

A significant drawback of relying heavily on rote learning in physics is its limited ability to foster genuinely transferable problem-solving skills. When students primarily focus on memorizing solution techniques for specific problems, they often struggle when confronted with even slightly modified scenarios. This is because the memorized procedures aren’t connected to a deeper understanding of the underlying physical principles; instead, they remain brittle and context-dependent. Consequently, a student might successfully solve a textbook problem but fail to apply the same concepts to a real-world situation or a novel problem that requires a creative approach. The emphasis on replicating known solutions, rather than analyzing the problem’s core elements and constructing a solution from first principles, ultimately hinders the development of adaptable and resilient problem-solving abilities-a critical skill for success in advanced physics and related fields.

Truly gauging a student’s grasp of fundamental physics principles demands assessment strategies that move beyond standard problem sets. Current evaluations often unintentionally test pattern recognition rather than conceptual understanding, as students may solve problems by applying memorized procedures to superficial variations. To address this, educators are increasingly focused on developing problem banks specifically designed to isolate core concepts. These banks utilize a limited number of underlying principles, presenting them through diverse mathematical representations and contextual scenarios, yet minimizing changes to the essential physics involved. By controlling for these superficial variations, assessment can more accurately pinpoint genuine conceptual mastery and predictive ability – the capacity to apply knowledge effectively to genuinely novel challenges, rather than simply replicating learned solutions.

The Automated Echo: Generating Problems at Scale

Large Language Models (LLMs) present a viable method for automatically generating isomorphic problem banks, which are sets of problems sharing the same underlying mathematical structure but differing in superficial details. This automation is achieved by training LLMs on datasets of existing problems and their solutions, enabling them to synthesize new problems conforming to specified parameters. The key benefit lies in the potential for scalable content creation; LLMs can rapidly produce a large number of unique problem instances, significantly reducing the manual effort traditionally required for curriculum development and assessment generation. Furthermore, LLMs can be conditioned to generate problems with controlled difficulty levels and varying parameters, allowing for the creation of personalized learning experiences and adaptive testing systems.

Prompt chaining addresses the complexity of automated content generation by breaking down the overall task into a series of interconnected prompts. Instead of relying on a single, comprehensive prompt to produce a complete output, this technique structures the generation process as a pipeline. Each prompt in the chain receives the output of the previous prompt as input, allowing for iterative refinement and control. This modular approach simplifies the creation of complex content, facilitates error diagnosis and correction within specific stages, and enables the application of different LLM capabilities to specialized sub-tasks, ultimately improving the quality and consistency of the generated content.

Integrating tool use with Large Language Models (LLMs) extends their generative capabilities by enabling access to external functions and APIs. This allows LLMs to move beyond purely textual generation and incorporate computational or data-driven constraints into the problem bank creation process. For example, a tool could verify the mathematical correctness of a generated equation, a physics simulation could validate the feasibility of a scenario, or an API call could retrieve real-world data to ground problem parameters. By offloading validation and constraint enforcement to these external tools, LLMs can significantly improve the accuracy, consistency, and overall validity of the generated problem variations, addressing limitations inherent in relying solely on the LLM’s internal knowledge and reasoning abilities.

The Mirage of Consistency: Validating What We Build

Difficulty homogeneity within generated problem banks is critical for reliable assessment; problems designed to evaluate the same underlying concept should consistently require a similar level of cognitive effort to solve. This ensures that variations in student performance reflect actual differences in understanding, rather than inconsistencies in problem difficulty. A lack of homogeneity introduces noise into the assessment, potentially misclassifying student proficiency and hindering accurate knowledge tracing. Establishing this consistency requires careful control during problem generation, followed by empirical validation using student performance data to identify and address any outliers or inconsistencies in difficulty levels.

Difficulty consistency within a generated problem bank can be quantitatively assessed using established statistical methods. Pearson Correlation can determine the linear relationship between problem completion rates or scores, indicating whether problems intended to test the same concept yield similar performance metrics; a high positive correlation suggests consistent difficulty. Item Response Theory (IRT) provides a more nuanced approach, modeling the probability of a correct response based on both student ability and problem difficulty; IRT parameters, specifically item difficulty and discrimination, allow for the precise comparison of problems and identification of outliers that deviate significantly from the expected difficulty level for a given concept. These methods require a statistically significant sample size of student responses to ensure reliable results.

Problem validation necessitates the collection and analysis of student performance data to empirically determine the effectiveness of generated questions. This data includes metrics such as accuracy rates, completion times, and common error patterns. Statistical analysis of these metrics allows for the quantification of problem difficulty and discrimination – the ability of a problem to differentiate between students with varying levels of understanding. Specifically, a statistically significant correlation between expected performance and actual student results indicates strong validation; conversely, discrepancies highlight potential issues with problem quality, clarity, or alignment with learning objectives. This iterative process of data collection and analysis informs refinement of the problem generation process and ensures the created problem bank accurately assesses intended skills.

The Promise of Adaptation: A Future of Personalized Physics

The creation of truly personalized physics education is becoming increasingly feasible through the automated generation of isomorphic problem banks. This innovative approach moves beyond static assessments by constructing numerous, structurally identical problems-isomorphs-that differ only in numerical values or superficial details. By dynamically generating these variations, educators can create tailored assessments that pinpoint a student’s conceptual grasp, rather than their ability to solve a specific, memorized problem. This ensures that evaluations accurately measure underlying understanding of physics principles, independent of rote memorization or mathematical manipulation skills. The technique effectively isolates the core concepts being tested, offering a more precise and nuanced evaluation of each student’s knowledge and identifying specific areas where targeted intervention can maximize learning potential.

The power of automatically generated problem banks extends beyond simply offering varied practice; it lies in the ability to dynamically adjust problem difficulty to suit individual student needs. By altering numerical values, physical constants, or even the complexity of the scenario within a given problem type, the system can create isomorphic problems that test the same underlying concepts at different cognitive demands. A student consistently solving problems with smaller values or simpler setups might be presented with increasingly complex scenarios, while a struggling learner receives modified problems that reinforce foundational understanding. This granular control over difficulty ensures that each student is consistently challenged at an appropriate level, preventing both frustration and boredom, and fostering a more effective and personalized learning experience.

The creation of isomorphic problem banks isn’t merely about generating practice questions; it unlocks the potential for truly adaptive learning systems. These systems dynamically assess a student’s evolving understanding and, crucially, respond with precisely tailored feedback and support. By pinpointing specific areas of difficulty – revealed through performance on varied problem iterations – the system can deliver targeted interventions, offering hints, explanations, or alternative problem approaches. This individualized approach contrasts sharply with traditional, one-size-fits-all instruction, and allows students to progress at their own pace, mastering concepts before moving forward. The result is a demonstrable maximization of learning outcomes, as students receive support exactly when and where they need it, fostering deeper conceptual understanding and sustained engagement with the material.

The Limits of Scale: Reasoning Towards Robust Systems

The capacity of large language models to generate complex and nuanced problems hinges significantly on advancements in instruction tuning and the development of models explicitly designed for reasoning. Through carefully crafted prompts and training data, these models are not simply memorizing patterns, but learning to apply logical steps and problem-solving strategies. This targeted approach moves beyond superficial question generation, allowing the models to create problems that require genuine cognitive effort – demanding more than recall, and instead emphasizing analytical skills. Consequently, the quality of generated problems increases, becoming more isomorphic and diverse, which is essential for robust assessment and truly personalized learning experiences. This focus on reasoning capability represents a pivotal shift, enabling LLMs to become powerful tools for both educational content creation and adaptive evaluation.

Research indicates that expanding the parameter count of large language models (LLMs) doesn’t simply improve performance-it fundamentally alters their capacity for complex reasoning. Larger models demonstrate a heightened ability to not only solve problems but also to generate a multitude of alternative, yet structurally equivalent, problems. This capability stems from the increased representational power afforded by greater scale, allowing the model to explore a broader solution space and identify isomorphic variations. Consequently, a sufficiently scaled LLM can create diverse problem sets that test the same underlying concepts in novel ways, effectively probing a student’s genuine understanding beyond rote memorization and fostering a more robust and adaptable skillset. This suggests that continued scaling remains a viable pathway toward increasingly sophisticated and versatile reasoning systems.

The advent of automated problem generation, powered by large language models, signals a paradigm shift in educational assessment. Rather than relying on static tests, future systems can dynamically tailor challenges to an individual’s evolving skill level, presenting increasingly complex problems as proficiency grows and revisiting foundational concepts where needed. This adaptive approach moves beyond simply measuring what a student knows to assessing their capacity for problem-solving and critical thinking in real-time. By continuously calibrating difficulty and content, these systems promise to unlock personalized learning experiences, maximizing engagement and fostering deeper understanding – ultimately moving away from a ‘one-size-fits-all’ model of education towards a more nuanced and effective system.

The pursuit of automated assessment, as detailed in this work, echoes a fundamental truth about complex systems. A system that never breaks is, indeed, a dead one. The framework’s ability to generate and validate isomorphic physics problems isn’t about achieving a flawless bank of questions; it’s about building a resilient ecosystem capable of adapting and evolving. The inherent potential for variation within the generated problems-a natural consequence of the GenAI approach-is not a bug, but a feature. It’s a recognition that true scalability lies not in perfect replication, but in managed imperfection, and the framework’s prompt chaining method demonstrates a willingness to embrace the unpredictable nature of creation. As Ken Thompson once said, “Debugging is twice as hard as writing the code in the first place. Therefore, if you write the code as cleverly as possible, you are, by definition, not smart enough to debug it.”

The Horizon of Problems

The facile success of automated problem generation, as demonstrated, is not a destination but a symptom. The system doesn’t solve the challenge of assessment; it merely shifts the locus of failure. Currently, the emphasis lies on generating isomorphic problems – variations on a theme. But isomorphism is a brittle property. A truly robust assessment doesn’t resist change, it anticipates it. The inevitable drift in underlying model assumptions, the slow corruption of the knowledge base, will not manifest as incorrect answers, but as subtly different questions.

The current framework treats prompts as directives, but views them as prophecies. Each carefully crafted instruction is a prediction of how the system will misinterpret, extrapolate, and ultimately, diverge from intended behavior. Long-term reliability isn’t achieved through validation against a fixed set of answers, but through continuous monitoring of the shape of the generated problems – identifying emerging patterns of distortion before they become critical failures.

The true scalability lies not in the quantity of problems generated, but in the capacity to observe and adapt to the evolving ecosystem of the Large Language Model itself. The system will not be perfected; it will become increasingly complex, increasingly unpredictable, and ultimately, increasingly interesting. The goal is not to build an assessment, but to cultivate a garden of problems, constantly pruned and reshaped by the forces of entropy and change.

Original article: https://arxiv.org/pdf/2602.05114.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/