Physics Proved by AI: A New Era for Automated Reasoning

Author: Denis Avetisyan

Researchers have developed a system that leverages artificial intelligence to formally prove physics theorems, pushing the boundaries of automated reasoning and mathematical problem-solving.

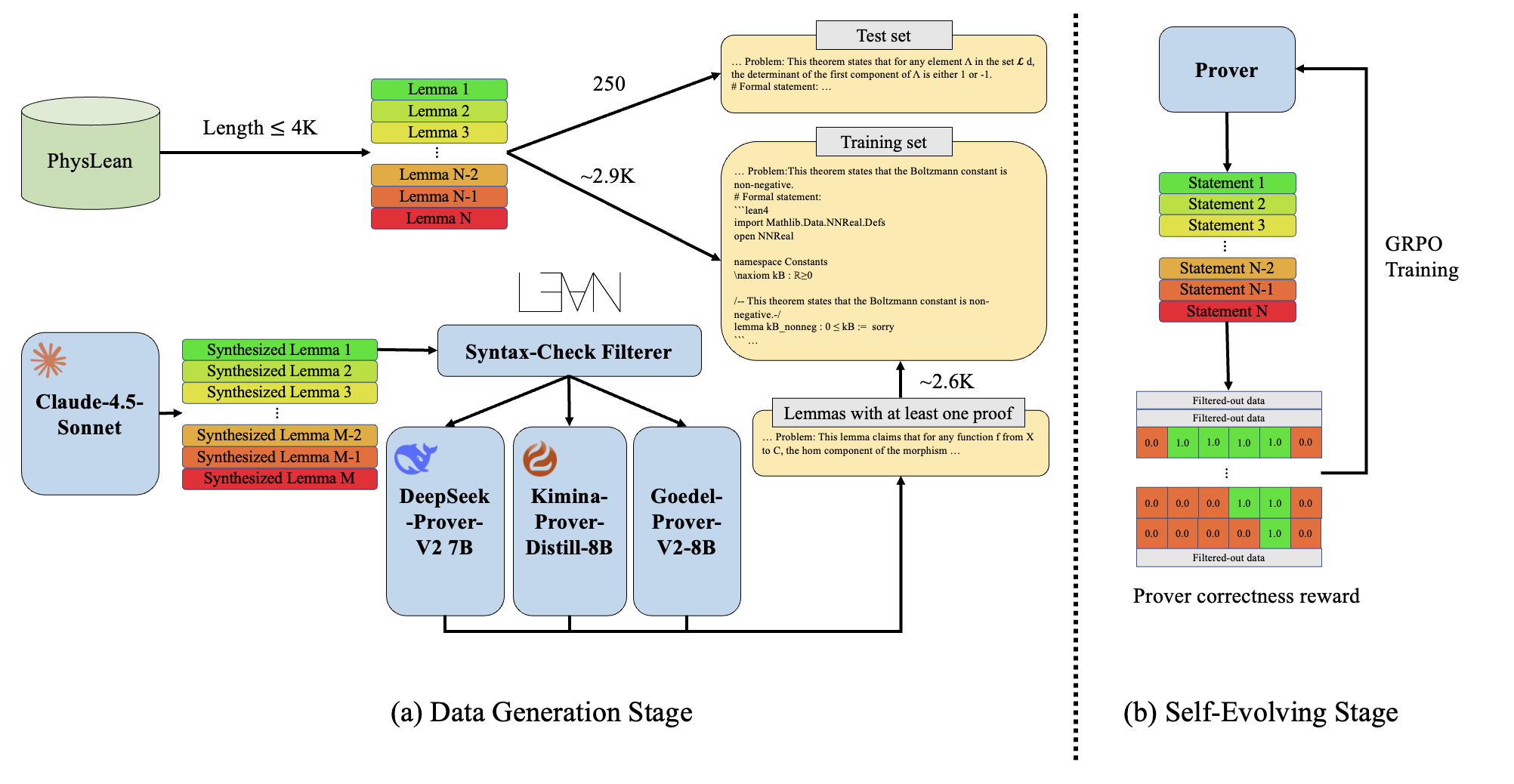
A physics prover framework systematically evolves automated reasoning capabilities by first constructing a training dataset of 5,541 statements-sourced from both existing formalized physics and synthetically generated lemmas validated by Lean’s syntax and proof-checking-and then employing a Graph-based Reinforcement Prover Optimizer (GRPO) trained on proof correctness as a reward signal, effectively bootstrapping a system capable of independently verifying physical principles.

This work introduces PhysProver, a formal theorem prover for physics built on large language models, reinforcement learning, and a novel physics-focused dataset.

While large language models excel at natural language reasoning and have begun to impact formal mathematics, their application to formal theorem proving within physics remains largely unexplored. This limitation motivates the work presented in ‘PhysProver: Advancing Automatic Theorem Proving for Physics’, which introduces a novel approach to enhance formal reasoning in the physics domain. By training the DeepSeek-Prover-V2-7B model with reinforcement learning on a dedicated dataset, PhysLeanData, PhysProver achieves a [latex]2.4\%[/latex] improvement across multiple physics sub-domains and demonstrates non-trivial generalization to mathematical benchmarks. Does this paradigm shift offer a viable pathway for extending the capabilities of formal provers beyond traditional mathematical disciplines and into the complexities of scientific reasoning?

Deconstructing the Foundations: The Limits of Formal Proof

The bedrock of physics relies on the unwavering certainty of its theories, demanding rigorous verification at every stage; however, the increasing complexity of modern physics presents a formidable challenge to traditional proof methods. While historically, physicists have relied on careful analysis, peer review, and experimental corroboration, these approaches struggle with the sheer length and intricacy of contemporary derivations, particularly those involving advanced mathematical frameworks like [latex]Quantum Field Theory[/latex] or [latex]General Relativity[/latex]. The potential for subtle errors to propagate through lengthy proofs is significant, and the human capacity for exhaustive checking is demonstrably limited. Consequently, a growing need exists for more robust and automated verification techniques capable of handling the scale and sophistication of modern physical theories, ensuring the continued reliability of this foundational science.

The painstaking process of translating the intuitive language of physics into the strict logic required for formal verification presents a significant bottleneck in modern research. While physicists routinely rely on mathematical derivations, these are often lengthy and complex, leaving room for subtle errors that can propagate through calculations and potentially invalidate entire theoretical frameworks. Manually formalizing these theories – essentially rebuilding each argument from first principles within a formal system – demands an enormous investment of time and expertise, diverting resources from the core task of scientific discovery. This meticulous, yet error-prone, undertaking frequently reveals inconsistencies that were previously overlooked, demanding further refinement and slowing the pace of progress in areas such as quantum field theory and general relativity. The sheer complexity of contemporary physics means that even seemingly minor mistakes can be exceptionally difficult to detect, highlighting the urgent need for automated or semi-automated formalization tools.

Current automated theorem provers, while powerful in formal logic and mathematics, often falter when applied to the intricacies of advanced physics. These systems typically lack the domain-specific knowledge – encompassing not just equations but also the underlying physical principles, intuitive assumptions, and nuanced interpretations – necessary to navigate complex proofs. Unlike mathematical proofs which rely on explicitly stated axioms, physical reasoning frequently employs implicit knowledge and relies on approximations or idealizations. Consequently, a theorem prover might struggle with seemingly straightforward physical derivations, requiring extensive manual guidance or adaptation. Furthermore, many physical theories involve continuous mathematics, infinite-dimensional spaces, and subtle topological considerations – areas where existing provers have limited capacity. Bridging this gap necessitates the development of new tools capable of representing physical knowledge effectively and reasoning with the unique challenges inherent in the discipline, potentially incorporating techniques from machine learning and symbolic regression to augment formal verification.

PhysProver: Reversing the Proof – An RL-Driven Approach

PhysProver represents a new approach to automated theorem proving, leveraging the capabilities of the DeepSeek-Prover-V2-7B large language model, which is publicly available under an open-source license. This foundation allows for community contribution and scrutiny of the system’s architecture and functionality. Rather than constructing a prover from scratch, PhysProver builds upon and adapts an existing, pre-trained model, enabling faster development and potentially improved performance through transfer learning. The choice of DeepSeek-Prover-V2-7B provides a baseline level of reasoning ability that is then refined through training on a specialized dataset, as opposed to requiring the model to learn both general language understanding and formal proof techniques simultaneously.

PhysProver employs Reinforcement Learning (RL) to automatically discover and refine strategies for constructing formal proofs. The system learns through interaction with a dataset comprising 5,541 formalized theorems, treating proof steps as actions within an environment. An RL agent is trained to maximize a reward function correlated with successful proof completion, effectively learning which sequences of proof tactics are most likely to yield valid results. This data-driven approach allows PhysProver to surpass the limitations of manually designed proof strategies and adapt to the complexities of automated theorem proving.

PhysLeanData serves as the training corpus for PhysProver, comprising 5,541 formalized theorems specifically within the domain of physics. This dataset is characterized by its expression of mathematical statements in the Lean4 proof assistant language, enabling machine-readability and facilitating the application of automated theorem proving techniques. The curation process involved translating physical principles and results into rigorous logical formulations suitable for Lean4, ensuring both mathematical correctness and representational clarity. The dataset’s composition focuses on a diverse range of physics topics, providing a broad foundation for the Reinforcement Learning agent to learn effective proof strategies applicable across multiple sub-disciplines.

Fine-Tuning the Algorithm: Constraining the Search Space

Group Relative Policy Optimization (GRPO) is utilized to address challenges inherent in reinforcement learning, specifically non-stationary policy distributions which can destabilize training. GRPO achieves this by maintaining a relative entropy constraint between the current policy and a reference policy representing the behavior of previous iterations. This constraint effectively regularizes policy updates, preventing drastic shifts that can lead to performance degradation. By optimizing a policy within this constrained space, GRPO facilitates more stable learning and accelerates convergence compared to traditional policy optimization methods. The algorithm computes a trust region update, limiting the divergence between successive policies and promoting consistent improvement throughout the training process.

Rejection Sampling Fine-tuning was implemented to improve training efficiency by selectively utilizing in-distribution data. This technique involves generating samples and then applying an acceptance/rejection criterion based on a learned density model, ensuring that only high-quality, representative data points are used for fine-tuning. By focusing on data confirmed to align with the expected input distribution, the algorithm minimizes the impact of potentially noisy or irrelevant samples, resulting in faster convergence and improved model performance. The acceptance rate is dynamically adjusted to balance sample quality and training speed, optimizing the fine-tuning process for the specific dataset and model architecture.

Chain-of-Thought Prompting improves model performance by encouraging the generation of intermediate reasoning steps prior to arriving at a final answer. This technique involves providing prompts that explicitly request a step-by-step explanation or justification of the thought process, effectively transforming the model into one that not only provides an answer, but also articulates how it reached that conclusion. By decomposing complex tasks into a series of smaller, more manageable steps, the model demonstrates increased accuracy and interpretability, particularly in tasks requiring multi-hop reasoning or logical inference. The approach relies on leveraging the model’s pre-existing knowledge and linguistic capabilities to construct a coherent and verifiable chain of thought, leading to more reliable and transparent results.

Beyond the Training Set: Generalization and the Future of Automated Discovery

PhysProver exhibits a noteworthy capacity for generalization, as demonstrated through evaluations on the MiniF2F benchmark – a dataset designed to assess performance on problems differing from those encountered during training. This ability to handle out-of-distribution data is crucial for real-world applicability, and PhysProver achieved over a 1% improvement in Pass@16 accuracy when compared to its base model. The Pass@16 metric indicates the probability of finding at least one correct solution within 16 attempts, and this increase signifies a tangible enhancement in the model’s robustness and problem-solving consistency when faced with novel physical scenarios. This result highlights not simply memorization of training examples, but a developing capacity to apply learned principles to previously unseen challenges.

The developed model demonstrates a significant advancement in problem-solving capabilities within the realm of physics, achieving an overall accuracy of 35.6% on a dedicated physics dataset. This result isn’t merely incremental; it surpasses the performance of current state-of-the-art mathematical provers by a margin of 2.4%. This improvement suggests the model is effectively learning and applying physical principles to solve complex problems, indicating a nuanced understanding beyond purely mathematical manipulation. The achievement highlights the potential for artificial intelligence to not only replicate, but also enhance, human reasoning in scientific domains, paving the way for automated assistance in physics research and education.

Continued development of this physics problem-solving model centers on two key strategies to address increasingly challenging scenarios. Researchers plan to substantially expand the training dataset, exposing the system to a wider range of physical principles and problem types, thereby enhancing its generalization capabilities. Simultaneously, exploration of more sophisticated reinforcement learning techniques is underway, aiming to refine the model’s reasoning process and enable it to decompose complex problems into manageable steps. This dual approach-data augmentation coupled with algorithmic advancement-promises to unlock the potential for tackling physics problems currently beyond the reach of automated systems, ultimately paving the way for a more robust and versatile artificial intelligence capable of scientific discovery.

The pursuit of automated reasoning, as demonstrated by PhysProver, isn’t about building infallible systems-it’s about meticulously dismantling assumptions until only verifiable truth remains. The project’s reliance on reinforcement learning to refine a large language model mirrors a process of controlled demolition, stress-testing the boundaries of both physics and mathematical logic. This resonates with Edsger W. Dijkstra’s observation: “It is not sufficient to prove that something works; you must also prove that it does not work.” The elegance of PhysProver lies not in its success rate, but in its systematic attempt to disprove existing theorems and identify weaknesses-a true exercise in reverse engineering reality, pushing the limits of formal theorem proving.

Beyond Proof: Charting Unseen Connections

The emergence of PhysProver, while demonstrating a notable stride in automated reasoning within physics, subtly underscores a far older problem: the limitations inherent in formalizing intuition. It isn’t merely about achieving proof, but about the very act of translation-rendering a physicist’s ‘sense’ of a solution into the rigid grammar of a theorem prover. The system excels by learning patterns, but genuine discovery often resides in the deviations, in the elegant violations of expectation. The next iteration must, therefore, actively cultivate a capacity for controlled error-a means of exploring the edges of logical consistency, rather than simply reinforcing it.

Current datasets, even those specifically constructed for physics, remain artifacts of pre-existing knowledge. They are, at best, maps of territories already charted. A truly robust system will need to generate its own problems-to pose questions that expose gaps in current understanding. This necessitates a shift from passive learning to active inquiry, a process akin to scientific hypothesis generation. The architecture must embrace the chaotic, recognizing that the most fruitful avenues of investigation are often obscured by noise.

Ultimately, PhysProver is a mirror. It reflects not only the structure of physical laws, but also the architecture of human reasoning. The challenge now lies in building a system that can not only solve problems, but also reframe them, revealing connections previously hidden within the seemingly intractable complexity of reality. It is a reminder that chaos is not an enemy, but a mirror of architecture reflecting unseen connections.

Original article: https://arxiv.org/pdf/2601.15737.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Deconstructing the Foundations: The Limits of Formal Proof

PhysProver: Reversing the Proof – An RL-Driven Approach

Fine-Tuning the Algorithm: Constraining the Search Space

Beyond the Training Set: Generalization and the Future of Automated Discovery

Beyond Proof: Charting Unseen Connections

See also: