Agents Learn to Count, But Struggle to Generalize

by

Author: Denis Avetisyan

New research reveals how artificial agents develop numerical communication through interaction, showcasing both impressive precision and inherent limitations in scaling to unseen numbers.

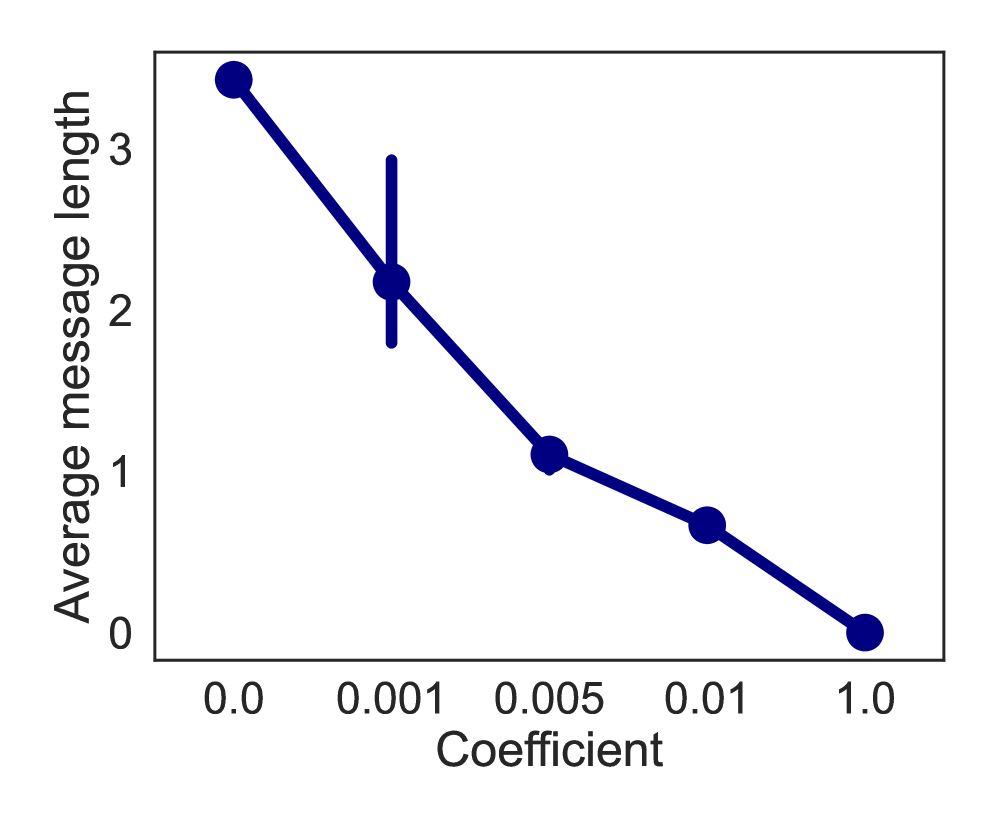
The study demonstrates that penalizing longer messages in a discrete communication system-trained on numerosities of one to five with a three-token vocabulary-induces a trade-off between accuracy and message length, as evidenced by a decreasing conditional entropy and average message length with increasing regularization coefficients.
The study demonstrates that penalizing longer messages in a discrete communication system-trained on numerosities of one to five with a three-token vocabulary-induces a trade-off between accuracy and message length, as evidenced by a decreasing conditional entropy and average message length with increasing regularization coefficients.

Artificial agents can emerge with a shared numerical code via interaction, but lack the compositional structure needed for robust generalization beyond trained values.

While human language efficiently encodes numerical concepts, it remains unclear whether communicative pressure alone can drive the emergence of similar representations in artificial agents. This is the central question addressed in ‘The emergence of numerical representations in communicating artificial agents’, which investigates how agents develop codes for representing quantities through interaction. The study demonstrates that agents can achieve precise communication of learned numerosities using both discrete and continuous signals, yet struggle to generalise to unseen numbers due to a lack of compositional structure in their emergent codes. Can additional pressures beyond simple communication foster the development of genuinely compositional and generalisable numerical systems in artificial intelligence?

The Foundations of Shared Quantity: Beyond Simple Signaling

Truly effective communication transcends the simple transmission of data; it necessitates a shared cognitive grasp of quantity, a concept known as ‘numerosity’. This isn’t merely about recognizing that a certain number of items are present, but rather a mutual understanding of how many. Research indicates that both humans and many animal species possess a surprisingly accurate, though limited, capacity to estimate quantities without counting, relying instead on approximate number systems. However, translating this internal representation into a communicative signal requires a receiver capable of interpreting that signal with a comparable understanding of quantity – a significant hurdle, as signals themselves are often arbitrary and divorced from the numerical value they represent. Consequently, successful communication isn’t just about sending a signal, but establishing a shared ‘number sense’ between sender and receiver, ensuring the intended quantity is accurately perceived.

Current communication systems, whether biological or artificial, frequently encounter limitations when conveying information about quantities not previously encountered. This inflexibility stems from the tendency to rely on fixed, pre-defined signals for specific amounts – a system that breaks down when faced with novel numerical values. Researchers are discovering that effective communication necessitates codes capable of generalization, allowing for the representation of an infinite range of quantities through compositional structures rather than discrete symbols. This demand for flexible codes extends beyond simple counting; it highlights a fundamental challenge in building systems that can adapt and communicate about the ever-changing numerical landscape of the world, prompting investigation into systems mirroring the compositional nature of human language where complex meanings are built from simpler components.

The difficulty in establishing robust communication systems isn’t simply about transmitting what is being communicated, but also how quantities are represented. A fundamental challenge lies in the arbitrariness of these symbolic representations; there’s no inherent reason why a particular sound or visual cue should signify ‘three’ or ‘seven’. This lack of natural connection necessitates a significant learning process for both the sender and receiver, demanding that they forge an association between abstract symbols and concrete quantities. Consequently, communication strategies are not built on intuitive understanding, but on memorization and learned convention, making the system vulnerable to errors and limiting its flexibility when encountering novel or complex numerical information. This reliance on learned associations presents a substantial hurdle in developing truly generalizable and efficient communication codes, particularly when dealing with systems that require representing an unbounded range of quantities.

Communication performance, measured by conditional entropy and accuracy, improves with balanced training data across classes, as demonstrated by experiments using sketches with varying numerosity and agent contexts.
Communication performance, measured by conditional entropy and accuracy, improves with balanced training data across classes, as demonstrated by experiments using sketches with varying numerosity and agent contexts.

The Referential Game: A Framework for Investigating Communication

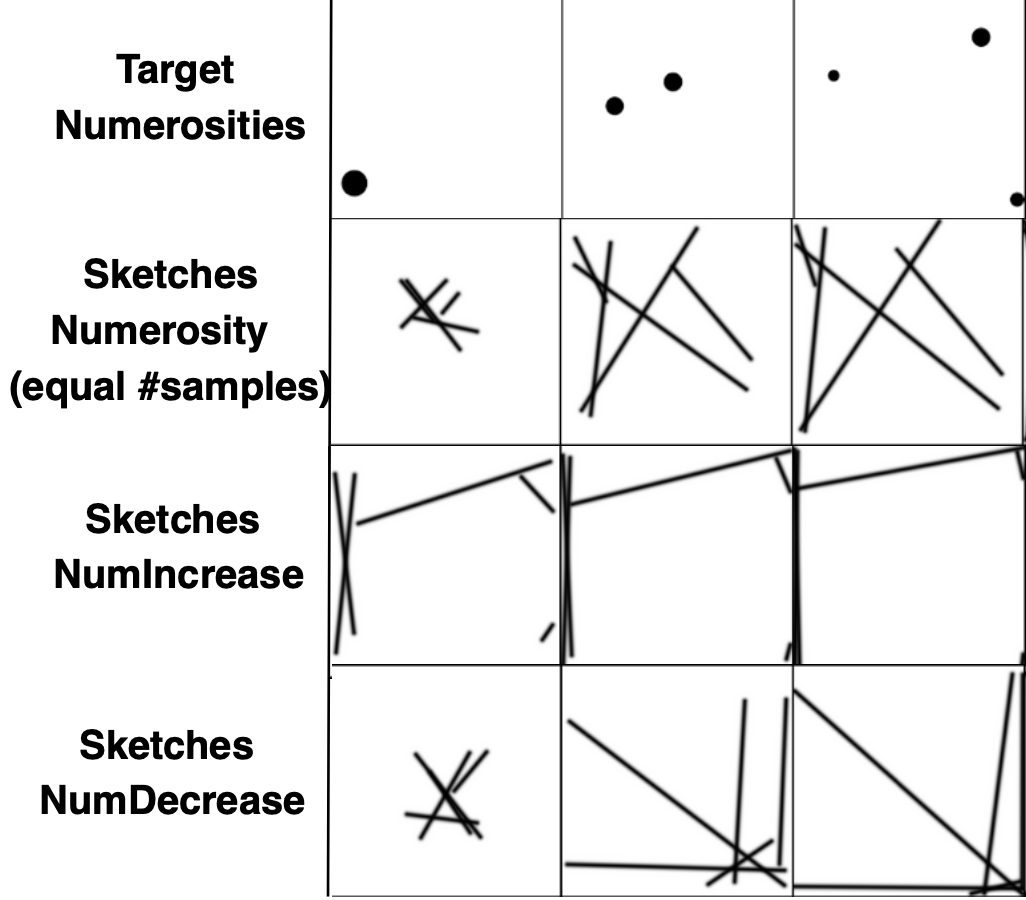
The Referential Game is a computational task used to investigate the emergence of communication strategies between artificial agents. In this setup, agents are required to convey information regarding the quantity, or ‘numerosity’, of visual stimuli to one another. The task is designed to assess how effectively agents can both encode and decode messages related to numerical values, and serves as a platform for studying the development of shared symbolic systems. Performance is measured by the receiver agent’s ability to accurately predict the numerosity based solely on the message received from the sender, allowing for quantitative analysis of communication success and the evaluation of different learning algorithms.

The communication framework utilizes neural network agents to facilitate learning through iterative interaction and error correction. These agents are trained using a multi-class hinge loss function, which penalizes incorrect classifications and encourages the development of effective communication strategies. The hinge loss operates by maximizing the margin between the correct class and the highest-scoring incorrect class, thereby promoting clear differentiation in communicated information. This loss function is applied to the agents’ outputs, guiding the adjustment of their internal parameters and improving their ability to both encode and decode messages over time. The agents learn to associate specific inputs with appropriate outputs, refining their communication protocols through repeated trials and feedback derived from the hinge loss calculation.

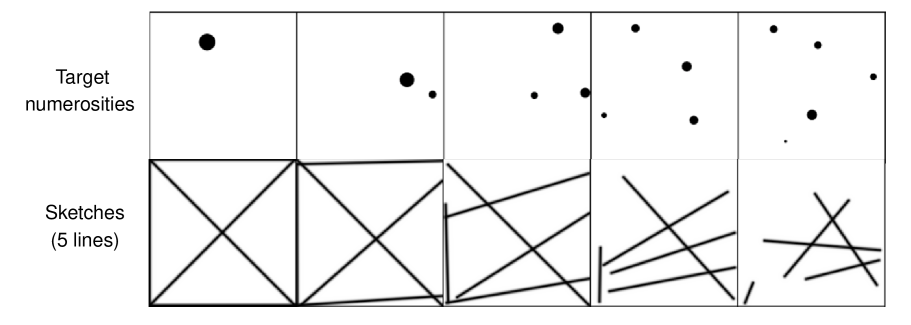
Communication within the referential game framework is facilitated through two distinct methods: discrete and continuous signaling. Discrete communication relies on a vocabulary of learned tokens; agents select from a predefined set of symbols to convey information about numerosity. Conversely, continuous communication allows agents to generate sketches – vector-based images – to represent the target quantity. These sketches are represented as continuous vectors, offering a potentially richer and more nuanced signaling space compared to the discrete token selection. Both methods are evaluated based on their ability to enable accurate information transfer between agents during the referential game task.

The referential game challenges a Receiver to identify a target numerosity from a set of five possibilities based on a discrete message from a Sender, even when the target instance differs from the Sender's view, as illustrated by example sketches representing numerosities from 1 to 5.
The referential game challenges a Receiver to identify a target numerosity from a set of five possibilities based on a discrete message from a Sender, even when the target instance differs from the Sender’s view, as illustrated by example sketches representing numerosities from 1 to 5.

Precision and Compositionality: The Building Blocks of Generalization

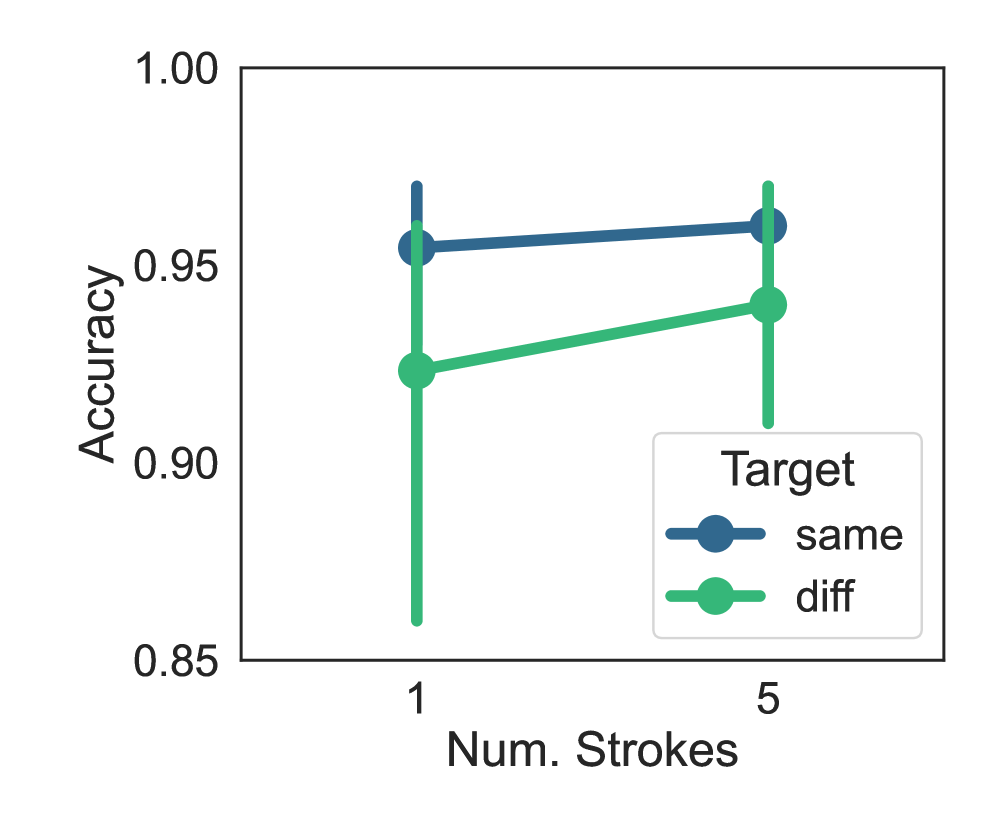
Communication precision, a critical metric for successful information transfer, refers to the unambiguous mapping of each signal to a specific quantity. This is quantitatively supported by minimizing [latex]Conditional Entropy[/latex], which measures the uncertainty in the receiver’s interpretation of a signal given the sender’s intent. Experimental results demonstrate that agents achieve high communication accuracy, particularly in the ‘Diff’ condition, where the sender and receiver observe different visual representations of the same numerosity. This suggests that agents can effectively generalize beyond specific visual instances and reliably convey quantities even when faced with variations in presentation, highlighting the importance of a robust signal-to-quantity mapping.

Compositionality, as a principle of communication, enables agents to represent a broader range of numerical values than those explicitly trained on. This is achieved by combining previously learned signals-representations of smaller quantities-to construct signals for larger, novel quantities. Rather than requiring separate training for each possible numerosity, compositionality allows the system to generalize by building complex representations from simpler components. This capacity is critical for scaling communication systems to handle an unbounded range of numerical values, as it avoids the need for exhaustive training data and promotes efficient representation of unseen quantities.

Agents employ distinct encoder architectures to process different input modalities for numerosity representation. Discrete signals are processed using Long Short-Term Memory (LSTM) encoders, which are recurrent neural networks designed to capture sequential dependencies within the input. Visual representations in the form of ‘Sketches’ are instead processed using Vision Transformer (ViT) encoders, leveraging a self-attention mechanism to identify relevant features within the image. Both encoder types ultimately translate these inputs into a numerical representation of the intended quantity, allowing for subsequent processing and comparison during communication tasks.

Communication accuracy, measured both discretely and continuously (via sketches), remains consistent whether agents are shown identical images (blue) or different images representing the same quantity (green), indicating the model effectively conveys numerosity from 1 to 5.
Communication accuracy, measured both discretely and continuously (via sketches), remains consistent whether agents are shown identical images (blue) or different images representing the same quantity (green), indicating the model effectively conveys numerosity from 1 to 5.

Beyond the Known: Exploring the Limits of Extrapolation

A fundamental aspect of any system learning to represent quantities lies in its ability to handle both familiar and novel values. When a system operates within the range of values it was trained on – for example, predicting a number between 1 and 10 after being trained on numbers 1 through 10 – this is known as interpolation. However, true intelligence requires moving beyond the known; when a system attempts to represent quantities outside its training range – predicting a value of 12 after training only on 1 through 10 – this is termed extrapolation. Successfully extrapolating demonstrates a deeper understanding of underlying principles, rather than simply memorizing training data, and is a critical measure of a system’s adaptability and generalization capabilities. The difficulty of extrapolation often surpasses that of interpolation, highlighting the challenge of applying learned knowledge to unseen scenarios.

Effective generalization, a hallmark of intelligent systems, relies on a capacity to not only understand data within the learned range – interpolation – but also to confidently extend that understanding to novel, unseen values – extrapolation. Recent research demonstrates this principle through sketch-based communication of numerosity, achieving a remarkably low conditional entropy of 1.348 even when conveying quantities outside the initial training set. This indicates a high degree of information efficiency; the system can communicate extrapolated values with minimal ambiguity. This ability to extrapolate, alongside interpolative accuracy, highlights the system’s robustness and flexibility in handling a broader range of numerical inputs, suggesting a capacity for adaptable and reliable communication beyond the confines of learned data.

The ease with which a numerical quantity is learned and communicated appears directly linked to its prevalence within the initial training data; quantities encountered more frequently are demonstrably easier for the system to both represent and convey. Analysis reveals that sketch-based representations diverge based on this training frequency, with heatmaps visualizing distinct patterns for common versus rare numerosities. This suggests the system doesn’t treat all numbers equally, instead prioritizing and refining its representation of those encountered most often during the learning phase – a phenomenon mirroring cognitive biases observed in human numerical processing. Consequently, the system’s ability to generalize beyond the training set is not uniform, exhibiting a tendency to more accurately represent and communicate frequently observed quantities.

The model successfully extrapolates numerosity beyond its training range of [latex]1-{20}[/latex] to 25, as demonstrated by consistent communication accuracy across both discrete extrapolation and interpolation tasks, leveraging a message previously optimized for the highest pretrained numerosity.
The model successfully extrapolates numerosity beyond its training range of [latex]1-{20}[/latex] to 25, as demonstrated by consistent communication accuracy across both discrete extrapolation and interpolation tasks, leveraging a message previously optimized for the highest pretrained numerosity.

The study illuminates how emergent communication systems, while capable of achieving precision, often lack the underlying structure for robust generalization. This mirrors a core tenet of scalable systems – clarity of idea over sheer power. As Tim Berners-Lee aptly stated, “The Web is more a social creation than a technical one.” The agents’ success in establishing a numerical code highlights the social aspect of communication, but their struggle with novel numbers reveals a critical limitation. Without compositional structure, the system, much like a poorly designed web, fails to scale beyond its initial training, demonstrating that a system’s behavior is fundamentally dictated by its structure.

Where Do We Go From Here?

The emergence of shared numerical codes, even rudimentary ones, from agent interaction is a compelling observation. However, the limitations revealed in generalisation beyond the training set are hardly surprising. A system built on memorisation, however elegant the initial interaction, will always falter when faced with true novelty. The research highlights a crucial point: arbitrariness in a code is not enough; it must be tethered to a structure that allows for flexible composition. The agents demonstrated a capacity for creating a code, but not the code – the one that maps seamlessly to underlying quantity, independent of specific instances.

Future work should move beyond simply observing code emergence and focus on architectural constraints that encourage compositional structure. The challenge lies not merely in getting agents to agree on a signal, but in building systems where that signal inherently embodies the principles of numerical representation. Perhaps inspiration can be drawn from the innate constraints present in human cognition – the inherent hierarchical structure of language, for example. A clever design, one feels, is usually a fragile one. Simplicity, a system built on fundamental principles, will likely prove more robust.

Ultimately, this line of inquiry points toward a deeper question: can true intelligence arise from interaction alone, or is there a necessary substrate of pre-existing structure? The answer, one suspects, lies somewhere in the elegant tension between these two forces. It is not enough to create a system that appears to understand number; the goal must be to build one that genuinely embodies it.

Original article: https://arxiv.org/pdf/2602.10996.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-13 00:27