Swarm Intelligence for Robotics: Finding the Best Path Forward

by

Author: Denis Avetisyan

A new optimization technique leverages the collective behavior of particle swarms to dramatically improve trajectory planning and achieve global optimality in robotic systems.

For long-horizon planning challenges, a Cross-Boundary Optimization (CBO) approach demonstrably outperforms the established Covariance Matrix Adaptation Evolution Strategy (CMA), as implemented in equations (18) and (19), achieving significantly superior results across the evaluated population at each iteration.
For long-horizon planning challenges, a Cross-Boundary Optimization (CBO) approach demonstrably outperforms the established Covariance Matrix Adaptation Evolution Strategy (CMA), as implemented in equations (18) and (19), achieving significantly superior results across the evaluated population at each iteration.

Consensus-based optimization (CBO) offers a robust solution to complex trajectory optimization problems by minimizing surrogate objectives through particle dynamics and consensus mechanisms.

Despite advances in trajectory optimization for robotics, many methods remain susceptible to local optima, hindering their ability to discover truly optimal solutions. This paper introduces ‘Consensus-based optimization (CBO): Towards Global Optimality in Robotics’, a novel zero-order optimization technique leveraging population dynamics to robustly converge towards global optima. Through theoretical analysis and benchmarks across challenging robotic scenarios-including long-horizon planning, dynamic balancing, and high-dimensional optimization-we demonstrate that CBO consistently outperforms existing methods. Could this approach unlock a new paradigm for global trajectory optimization and enable more sophisticated robotic behaviors?

The Illusion of Optimality

Trajectory Optimization, the process of determining the ideal sequence of movements for a robotic system, underpins the execution of increasingly complex tasks – from autonomous navigation and surgical procedures to dexterous manipulation and advanced assembly. However, achieving this optimality is a significant computational hurdle; as the complexity of the task – and therefore the length of the planned trajectory, or ‘horizon’ – increases, the number of possible control sequences explodes, demanding exponentially more processing power. This computational expense stems from the need to evaluate numerous potential trajectories, assess their performance against desired goals, and iteratively refine the control inputs to minimize errors and maximize efficiency. Consequently, finding truly optimal solutions often proves intractable, forcing engineers to rely on approximations or simplified models, potentially sacrificing performance or robustness in real-world applications.

Trajectory optimization, vital for enabling robots to perform intricate tasks, faces significant hurdles when planning over extended periods – a concept known as Long Horizon Planning. The core difficulty stems from the cumulative effect of small errors; each incremental step in a long sequence introduces a degree of uncertainty, and these inaccuracies compound over time, ultimately leading to drastically suboptimal or even failed trajectories. Furthermore, the problem’s dimensionality increases exponentially with the number of degrees of freedom in the robot and the length of the planned sequence, creating a computationally intractable space to search for an ideal solution. This ‘curse of dimensionality’ means that even modest increases in planning horizon or robot complexity can render traditional optimization methods prohibitively slow or require massive computational resources, limiting their applicability to real-world robotic systems.

Gradient-based optimization techniques, while computationally efficient for trajectory optimization, present significant hurdles in practice. These methods rely on iteratively adjusting control sequences in the direction of the steepest descent – or ascent – of a cost function, but this process is highly sensitive to initial conditions and parameter tuning. The algorithms can easily become trapped in local minima, yielding suboptimal solutions that appear ideal within a limited scope but fail to achieve the global best. Furthermore, enforcing constraints – such as joint limits for a robotic arm or collision avoidance – often necessitates complex penalty functions or projection steps, further complicating the optimization process and potentially hindering convergence. Consequently, achieving robust and reliable performance with gradient-based methods demands considerable expertise and careful calibration for each specific robotic system and task.

The limitations of gradient-based trajectory optimization necessitate exploration of alternative approaches, especially when dealing with real-world robotic systems operating in unpredictable environments. These systems often present scenarios where obtaining accurate gradient information is difficult or impossible due to sensor noise, model inaccuracies, or the complexity of the dynamics themselves. Consequently, researchers are investigating derivative-free optimization techniques, such as evolutionary algorithms and reinforcement learning, that can navigate the search space without relying on explicit gradient calculations. These methods, while potentially more computationally demanding, offer robustness and the capacity to handle complex constraints and non-differentiable cost functions, paving the way for more adaptable and reliable robotic control in challenging and uncertain conditions.

Optimization using CBO successfully generates a 2-second G1 humanoid trajectory for free locomotion, as demonstrated by the progression from start to end positions (with target positions indicated by the shadowed silhouette).
Optimization using CBO successfully generates a 2-second G1 humanoid trajectory for free locomotion, as demonstrated by the progression from start to end positions (with target positions indicated by the shadowed silhouette).

The Allure of Gradient-Free Methods

Zero-order optimization methods represent a class of algorithms that estimate the optimal solution to a problem without requiring explicit gradient calculations. These methods operate solely on function evaluations – determining the output of a function for given inputs – and utilize this information to iteratively refine the search for the minimum or maximum value. This characteristic makes them particularly advantageous in scenarios where gradient information is unavailable, unreliable, or computationally expensive to obtain, such as in black-box optimization, problems with noisy objective functions, or when dealing with discrete or non-differentiable functions. Consequently, zero-order methods broaden the applicability of optimization techniques to a wider range of real-world problems compared to gradient-based approaches.

Model Predictive Path Integral (MPPI) and Covariance Matrix Adaptation Evolution Strategy (CMA-ES) are both established derivative-free optimization techniques. MPPI is a trajectory optimization method that utilizes a reinforcement learning approach, sampling multiple trajectories and weighting them based on their cost and a noise process; it excels in continuous control problems with relatively low dimensionality. CMA-ES, conversely, is an evolutionary algorithm that adapts the covariance matrix of a multivariate normal distribution to guide the search process; it demonstrates strong performance in high-dimensional, black-box optimization, but can be sensitive to the choice of initial covariance matrix and step size adaptation parameters. While both methods avoid gradient calculations, MPPI typically requires more function evaluations per iteration but can benefit from parallelization, whereas CMA-ES often converges more slowly but with greater robustness in complex landscapes.

Derivative-free optimization methods, while versatile, exhibit computational scaling issues related to problem dimensionality and dynamic complexity. The number of function evaluations required for convergence generally increases with the number of optimization variables, leading to a high computational cost in high-dimensional state spaces. Furthermore, complex dynamics – characterized by non-linearities, constraints, or multiple interacting variables – necessitate a greater number of evaluations to accurately estimate the objective function and its sensitivities, compounding the computational burden. This is because these methods rely on sampling the function space to approximate gradients or perform direct search, making them less efficient than gradient-based methods when gradients are available.

Current research in trajectory optimization is heavily focused on developing new algorithms to address limitations in computational efficiency and robustness. Existing derivative-free methods, while capable of handling problems without gradient information, often struggle with the curse of dimensionality and can be sensitive to noise or uncertainties in the system dynamics. Novel algorithms aim to mitigate these issues through techniques such as adaptive sampling strategies, surrogate modeling, and the incorporation of problem-specific knowledge. Improvements in efficiency are typically measured by reductions in the number of function evaluations required to reach a satisfactory solution, while robustness is assessed by the algorithm’s ability to consistently find feasible and near-optimal trajectories despite perturbations or model inaccuracies. These advancements are crucial for applying trajectory optimization to increasingly complex real-world scenarios.

While both MPPI and CMA fail to navigate the obstacle course and reach the tunnel, CBO successfully avoids all barriers and completes the task across varying environmental configurations.
While both MPPI and CMA fail to navigate the obstacle course and reach the tunnel, CBO successfully avoids all barriers and completes the task across varying environmental configurations.

Consensus-Based Optimization: A Different Approach

Consensus-Based Optimization (CBO) utilizes a population-based approach, maintaining a set of candidate solutions that evolve iteratively to locate optimal values. This method efficiently explores the solution space by evaluating multiple potential solutions concurrently and combining their information. Crucially, CBO employs surrogate objective minimization, meaning it approximates the true objective function with a simpler, computationally cheaper surrogate model. This allows for faster evaluation of candidate solutions, particularly in scenarios where the true objective function is expensive to compute. The surrogate model is updated as new solutions are evaluated, improving its accuracy and guiding the population towards promising regions of the solution space.

Consensus-Based Optimization (CBO) utilizes a communication protocol where each candidate solution within a population shares information with its peers to establish a collective understanding of the optimization landscape. This is achieved by each solution broadcasting its current best estimate of the objective function and related parameters; a consensus value is then computed, typically through averaging or a weighted sum, to create a shared, refined estimate. By incorporating this collective knowledge, individual solutions can more effectively adjust their search direction and accelerate convergence towards optimal solutions, as the consensus value provides a more robust and accurate representation of the solution space than relying solely on individual evaluations.

Consensus-Based Optimization (CBO) distinguishes itself from numerous optimization techniques by eliminating the need for explicit contact constraint handling. Traditional methods often require the formulation and enforcement of constraints to prevent the penetration of objects or ensure physically plausible solutions. CBO, however, implicitly satisfies these constraints through the consensus mechanism and population-based search, allowing it to directly address ‘Contact Implicit Optimization’ problems where contact constraints are not explicitly defined within the optimization formulation. This simplification streamlines the optimization process, reduces computational overhead, and broadens the applicability of CBO to a wider range of scenarios, particularly those involving complex contact interactions.

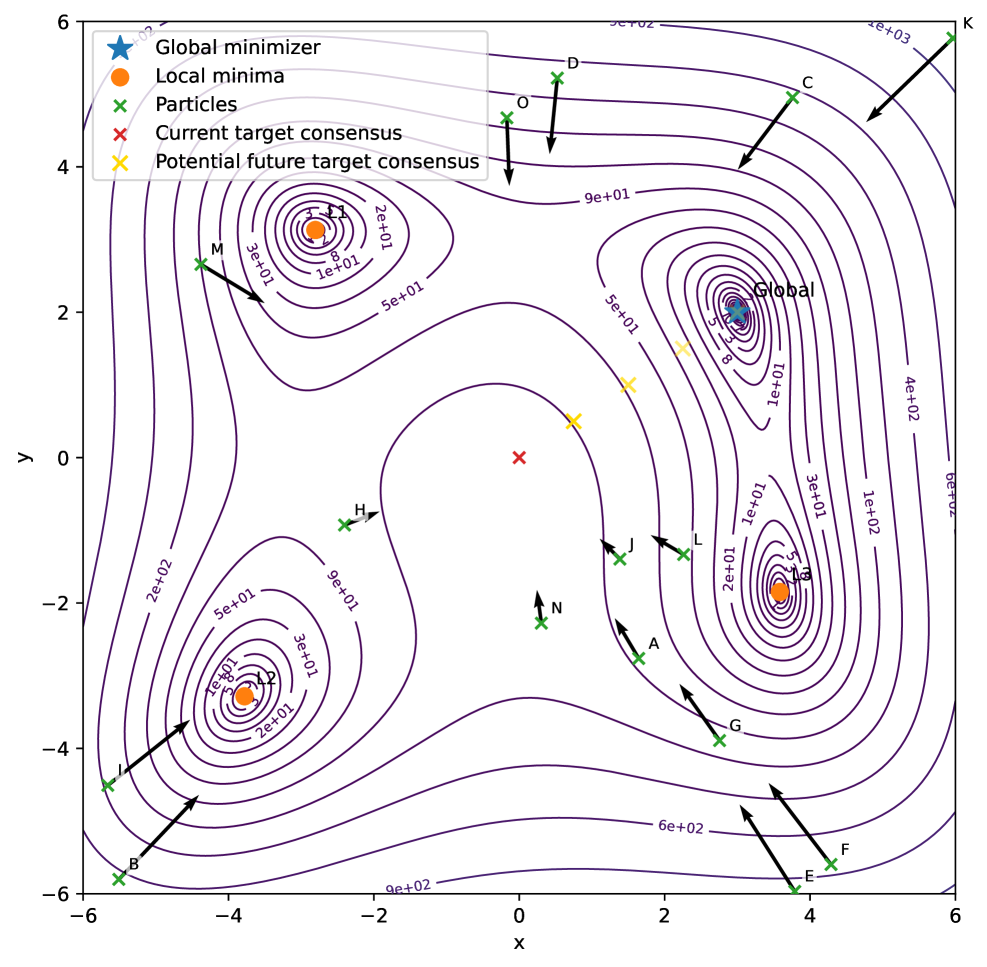
Performance analysis of the Consensus-Based Optimization (CBO) algorithm was conducted using standard benchmark functions, including the Himmelblau function – a four-dimensional test case characterized by a complex, highly curved solution space and a single global minimum. Rigorous testing with such functions demonstrates CBO’s capacity to effectively navigate non-convex landscapes and locate optimal or near-optimal solutions. Quantitative results, derived from repeated trials across various starting points, indicate a consistent ability to converge towards the global minimum with a defined level of accuracy and computational efficiency, validating the algorithm’s robustness and scalability for complex optimization problems.

This contour plot illustrates how the Centralized Batch Optimization (CBO) method, indicated by the star, effectively navigates a cost function landscape to outperform several local optimization approaches.
This contour plot illustrates how the Centralized Batch Optimization (CBO) method, indicated by the star, effectively navigates a cost function landscape to outperform several local optimization approaches.

The Devil is in the Details: Convergence and Evaluation

Central to validating the Constrained Bayesian Optimization (CBO) algorithm is a rigorous proof of convergence achieved through Lyapunov Function analysis. This mathematical technique establishes the system’s stability by demonstrating that a defined Lyapunov function-a scalar function whose value decreases over time-guarantees the algorithm will consistently approach an optimal solution. The analysis doesn’t merely suggest CBO might converge, but provides theoretical guarantees regarding its performance, ensuring it avoids oscillations or divergence during the optimization process. By formally demonstrating convergence, researchers establish a solid foundation for CBO’s reliability and predictability, setting it apart from empirical approaches and offering assurance of consistent, stable performance even in complex optimization landscapes. This analytical validation is crucial for deploying CBO in safety-critical applications where predictable behavior is paramount.

Assessing the speed at which an optimization algorithm approaches a solution requires a metric sensitive to the distribution of possible outcomes, and the Wasserstein distance – also known as the Earth Mover’s Distance – proves particularly well-suited for this purpose. Unlike simpler measures that only consider point-wise differences, the Wasserstein distance quantifies the minimum ‘cost’ of transforming one probability distribution into another, effectively measuring the ‘distance’ between the algorithm’s current state and the optimal solution’s distribution. This is especially crucial in complex optimization problems where multiple solutions might exist, or where the solution space is non-Euclidean. By employing the Wasserstein distance, researchers gain a robust and meaningful evaluation of the algorithm’s convergence rate, revealing not just if a solution is found, but how efficiently the algorithm navigates the probabilistic landscape towards optimality – a critical factor for real-world applications demanding both accuracy and speed.

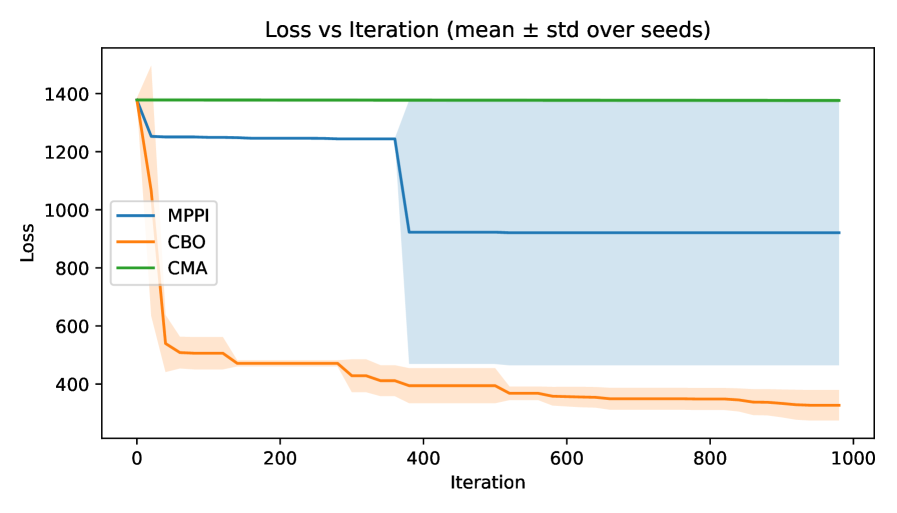
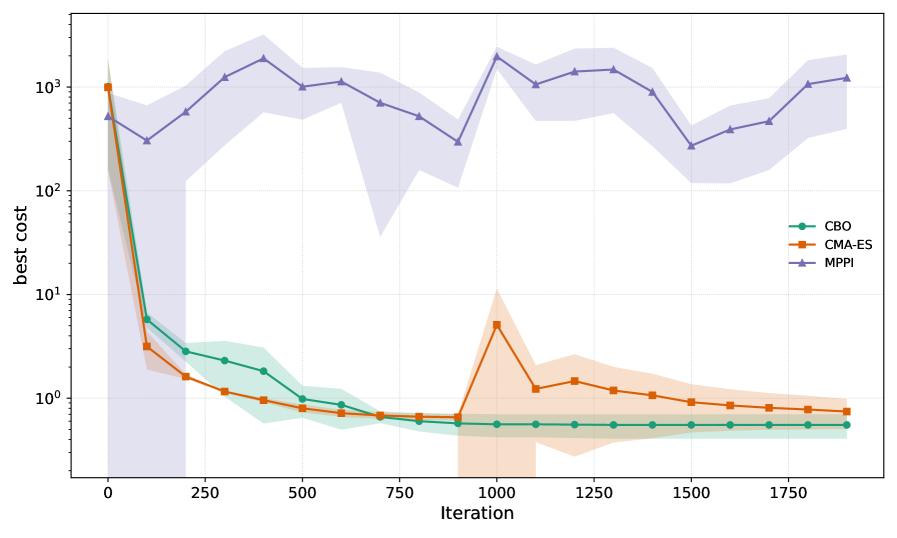
Evaluations reveal that the developed Constrained Bayesian Optimization (CBO) algorithm presents a viable and effective alternative to established zero-order optimization techniques. Across a series of rigorous experiments, CBO consistently achieved a substantial reduction in cost function values compared to benchmark methods. Notably, CBO outperformed both Model Predictive Path Integral (MPPI) and Covariance Matrix Adaptation Evolution Strategy (CMA-ES) in terms of optimization efficiency and solution quality. This performance advantage was particularly evident in complex, high-dimensional scenarios, such as 23-degree-of-freedom humanoid simulations, where MPPI and CMA-ES encountered significant difficulties; CBO, however, consistently succeeded in optimizing trajectories, highlighting its robustness and potential for application in challenging robotic control tasks.

Complex trajectory optimization for high-dimensional systems, such as 23-degree-of-freedom humanoid robots, often presents significant challenges for conventional zero-order methods. Recent investigations reveal that algorithms like Model Predictive Path Integral (MPPI) and Covariance Matrix Adaptation Evolution Strategy (CMA-ES) encounter difficulties in these scenarios, frequently failing to converge to viable solutions. However, the proposed approach, denoted as CBO, demonstrably succeeds in optimizing trajectories for these complex humanoids where its counterparts falter. This success isn’t merely qualitative; CBO consistently generates feasible and effective trajectories, highlighting its inherent robustness and superior performance in tackling the intricacies of high-dimensional, dynamic systems. The ability to navigate such challenging simulations underscores CBO’s potential as a valuable tool for advanced robotics and control applications.

Across the benchmark double-cartpole task, the CBO algorithm consistently outperforms CMA-ES with lower variance, indicating more reliable performance.
Across the benchmark double-cartpole task, the CBO algorithm consistently outperforms CMA-ES with lower variance, indicating more reliable performance.

The pursuit of global optimality, as this paper champions with Consensus-Based Optimization, feels…familiar. It’s a predictable arc. They’ll tout improved trajectory optimization, claim a breakthrough in robotics, and soon enough, production will introduce a new sensor, a slightly different load, or, heaven forbid, users will do something unexpected. Then, the elegant particle dynamics will be wrestling with a reality it wasn’t designed for. Donald Davies famously said, “The computer is a machine for making fast mistakes.” It’s a bleak truth, but applicable here. This CBO method, with its surrogate objective minimization, may find a local peak with admirable efficiency, but it’s only a matter of time before the real world demonstrates that optimality is a fleeting illusion. They’ll call it AI and raise funding, of course.

Beyond the Horizon

The promise of global optimality is, predictably, appealing. This work demonstrates an advance in trajectory optimization, but the truly interesting problems will emerge when deployed beyond controlled simulations. Any system predicated on a ‘consensus’ will inevitably discover the limits of that agreement. It will be fascinating to observe the first instance where the particle swarm prioritizes a locally optimal, yet spectacularly inefficient, solution simply because it is universally agreed upon. Anything self-healing just hasn’t broken yet.

The current framework, while an improvement on existing zero-order methods, still relies on a population-based approach. This introduces the usual scaling challenges. As robotic systems become more complex, the computational cost of maintaining consensus across a sufficiently large particle swarm will become prohibitive. The inevitable response will be attempts at ‘selective consensus’ – algorithms that cherry-pick agreement, effectively reintroducing the biases this approach seeks to avoid.

Documentation for these algorithms, of course, will remain a collective self-delusion. If a bug is reproducible, it implies a stable system – a rare and cherished state. The true measure of success will not be the elegance of the optimization, but the robustness of the failure modes when the inevitable occurs. The next step isn’t necessarily better optimization, but a more honest accounting of the chaos inherent in complex systems.

Original article: https://arxiv.org/pdf/2602.06868.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-10 08:26