Uncovering Hidden Order: AI’s New Lens on Physical Data

by

Author: Denis Avetisyan

Researchers are harnessing the power of artificial intelligence to identify underlying symmetries and reduce complexity in datasets, offering a novel approach to understanding the fundamental structure of physical phenomena.

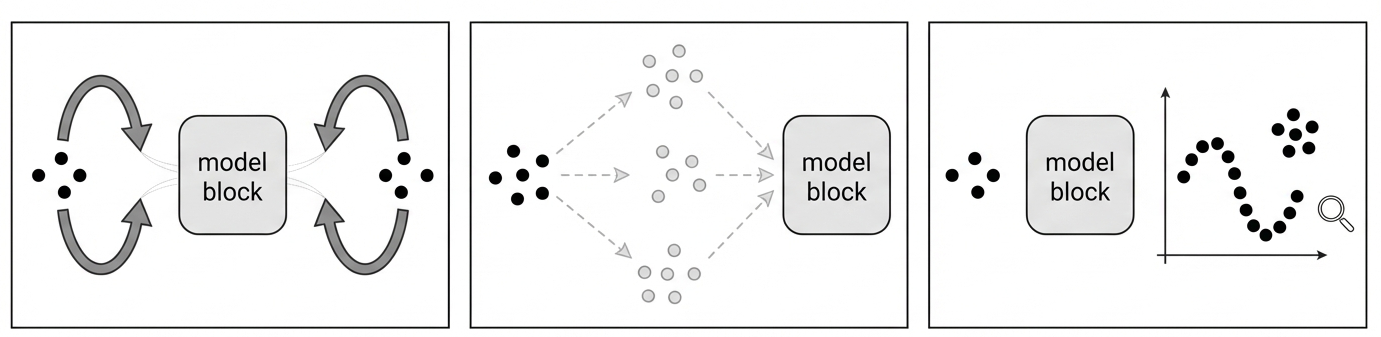
Symmetry within machine learning manifests across three distinct approaches: architectural imposition of invariance, implicit introduction through data manipulation, and emergent organization arising within latent spaces-a progression where control gives way to the spontaneous formation of order without explicit design.
Symmetry within machine learning manifests across three distinct approaches: architectural imposition of invariance, implicit introduction through data manipulation, and emergent organization arising within latent spaces-a progression where control gives way to the spontaneous formation of order without explicit design.

This review explores the use of variational autoencoders for symmetry detection, representation learning, and dimensionality reduction in scientific data analysis.

Despite the central role of symmetry in organizing physical laws and reducing complexity, identifying these underlying principles from data remains a significant challenge. This review, ‘Artificial Intelligence and Symmetries: Learning, Encoding, and Discovering Structure in Physical Data’, explores the emerging intersection of symmetry principles and modern machine learning techniques, particularly variational autoencoders, to address this issue. We demonstrate how data-driven approaches can reveal symmetry-induced dimensionality reduction through the self-organization of latent spaces, offering a complementary perspective to traditional theoretical methods. Can these techniques ultimately provide a pathway to automatically infer fundamental symmetries directly from complex physical datasets, bypassing the need for explicit inductive biases?

The Universe Whispers of Order

The universe, at its most fundamental level, operates according to principles of symmetry, where transformations leaving a physical system unchanged correspond to conserved quantities. This isn’t merely an aesthetic preference of nature; it’s a deeply ingrained rule. For instance, the homogeneity of space – the idea that physics doesn’t change with location – dictates the conservation of linear momentum. Similarly, the uniformity of time leads to energy conservation, and rotational symmetry ensures angular momentum remains constant. [latex]E = mc^2[/latex] itself, a cornerstone of modern physics, arises from the symmetry between space and time. These symmetries don’t just simplify equations; they provide powerful constraints, allowing physicists to predict behavior and understand complex systems by focusing on the invariant properties rather than the details of change. This principle extends beyond classical mechanics into quantum field theory and particle physics, providing a framework for classifying particles and interactions based on their symmetry properties.

The elegance of physical laws, often expressed through symmetry, frequently clashes with the inherent disorder of observed data. Real-world measurements are rarely perfect reflections of underlying principles; instead, they are riddled with noise, imperfections, and deviations that disrupt idealized symmetries. This ‘symmetry breaking’ manifests in various ways – a slightly asymmetric distribution of particles, a fluctuating signal, or seemingly random variations in a pattern – and introduces significant challenges for analysis. Consequently, techniques designed to exploit symmetry must account for these imperfections, often requiring complex algorithms to filter noise, identify true underlying patterns, and extract meaningful information from otherwise chaotic datasets. Addressing this discrepancy between theoretical symmetry and empirical messiness is therefore paramount to accurate modeling and robust data interpretation.

Effective data representation hinges on recognizing inherent symmetries within a system, or, crucially, acknowledging when those symmetries are absent. Data often reflects underlying physical laws governed by these principles; a rotating sphere, for instance, possesses radial symmetry which simplifies its description. However, real-world measurements are invariably subject to noise and external influences that break these symmetries. Failing to account for this symmetry breaking can lead to inaccurate models and flawed interpretations; a slightly deformed sphere requires a more complex representation than its perfectly symmetrical counterpart. Therefore, sophisticated data analysis techniques prioritize identifying and characterizing both the symmetries that remain and the ways in which they are disrupted, enabling a more concise, accurate, and ultimately useful portrayal of complex phenomena.

Current data science endeavors increasingly focus on harnessing the power of symmetry to refine analytical methodologies. Researchers are developing algorithms that actively seek and exploit inherent symmetries within datasets, dramatically reducing computational load and improving the accuracy of models. This approach moves beyond simply acknowledging symmetry; it integrates it directly into the data processing pipeline. By recognizing patterns and redundancies dictated by symmetry, these techniques require less data for training and generalize more effectively to unseen examples. Furthermore, robust data analysis now incorporates methods for gracefully handling symmetry breaking – the inevitable deviations from perfect symmetry found in real-world phenomena – ensuring that analytical outcomes remain reliable even with imperfect or noisy data. The ultimate goal is not merely to describe data, but to build predictive models that are both efficient and resilient, leveraging the fundamental principles of symmetry as a cornerstone of modern data science.

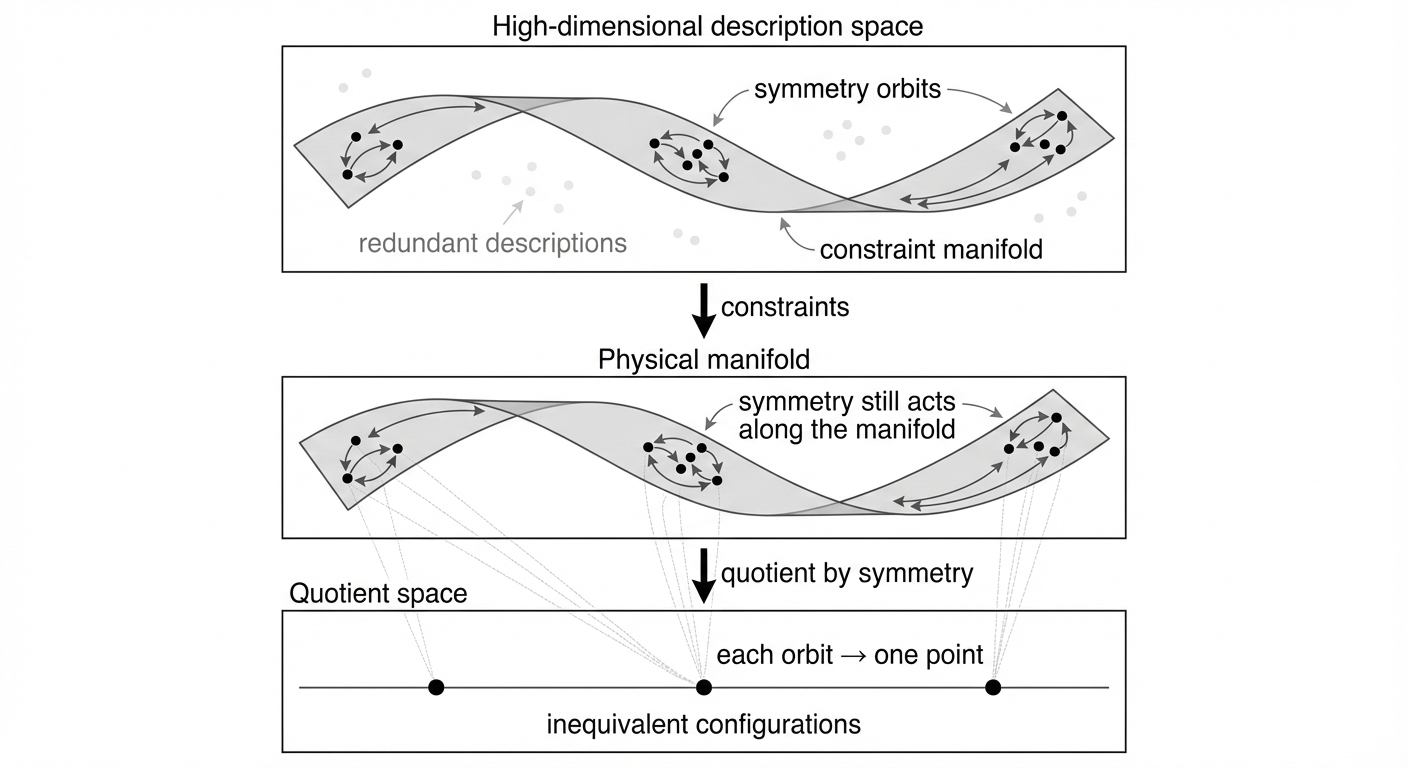
Symmetry reduces the dimensionality of physically possible configurations by identifying equivalent states and further restricting the data to physically inequivalent degrees of freedom, effectively distilling information from a high-dimensional space.
Symmetry reduces the dimensionality of physically possible configurations by identifying equivalent states and further restricting the data to physically inequivalent degrees of freedom, effectively distilling information from a high-dimensional space.

Reducing Complexity Through Invariance

Traditional dimensionality reduction techniques, such as Principal Component Analysis and autoencoders, operate by identifying and retaining the most significant axes of variance within a dataset. These methods typically assume each input variable represents an independent degree of freedom and, consequently, treat all variables as equally informative during the simplification process. This approach can be computationally inefficient and may fail to exploit inherent relationships or constraints within the data. By not accounting for potential redundancies or correlations among variables, these techniques may retain dimensions that contribute little to the overall representation of the data, hindering performance and interpretability. Consequently, applying domain-specific knowledge to prioritize or eliminate variables before or during dimensionality reduction can substantially improve the efficiency and accuracy of the resulting simplified dataset.

Symmetry within a dataset implies the existence of relationships between variables that reduce the number of independent parameters needed to describe the system. This reduction arises because symmetric transformations leave certain properties invariant, meaning that changes along one or more dimensions can be predicted from changes in others. Consequently, dimensions involved in symmetric relationships represent redundant degrees of freedom; the information they contain is already encoded within the remaining, independent dimensions. Exploiting these symmetries during dimensionality reduction can therefore minimize information loss and improve the efficiency of the process by focusing analysis on the truly independent variables defining the data’s structure.

Our analysis demonstrates a quantifiable relationship between effective dimensionality – the number of independent variables genuinely contributing to a system’s behavior – and established physical constraints. Specifically, systems governed by conservation laws, such as conservation of energy, momentum, or angular momentum in particle physics, exhibit a reduced effective dimensionality corresponding to the number of remaining independent degrees of freedom after applying those constraints. Similarly, in geometric systems, symmetries like translational or rotational invariance constrain possible configurations, lowering the effective dimensionality from the initial parameter space. This correspondence is not merely qualitative; we observe a direct numerical link between the reduction in dimensionality and the number of independent constraints imposed by these fundamental laws, validating the utility of dimensionality reduction as a means of identifying and exploiting underlying system symmetries.

Standard Principal Component Analysis (PCA) identifies orthogonal linear combinations of variables that capture maximum variance; however, it does not inherently account for known symmetries within the data. Incorporating symmetry constraints into PCA, such as requiring principal components to transform according to specific symmetry groups, reduces the search space for optimal components. This constrained optimization leads to more efficient computation, particularly in high-dimensional datasets, and can result in more physically or geometrically meaningful principal components. The efficiency gains stem from reducing the number of free parameters in the PCA optimization problem and preventing the algorithm from exploring solutions that violate established symmetry principles. Furthermore, the resulting components are often more robust and interpretable due to the explicit enforcement of these constraints.

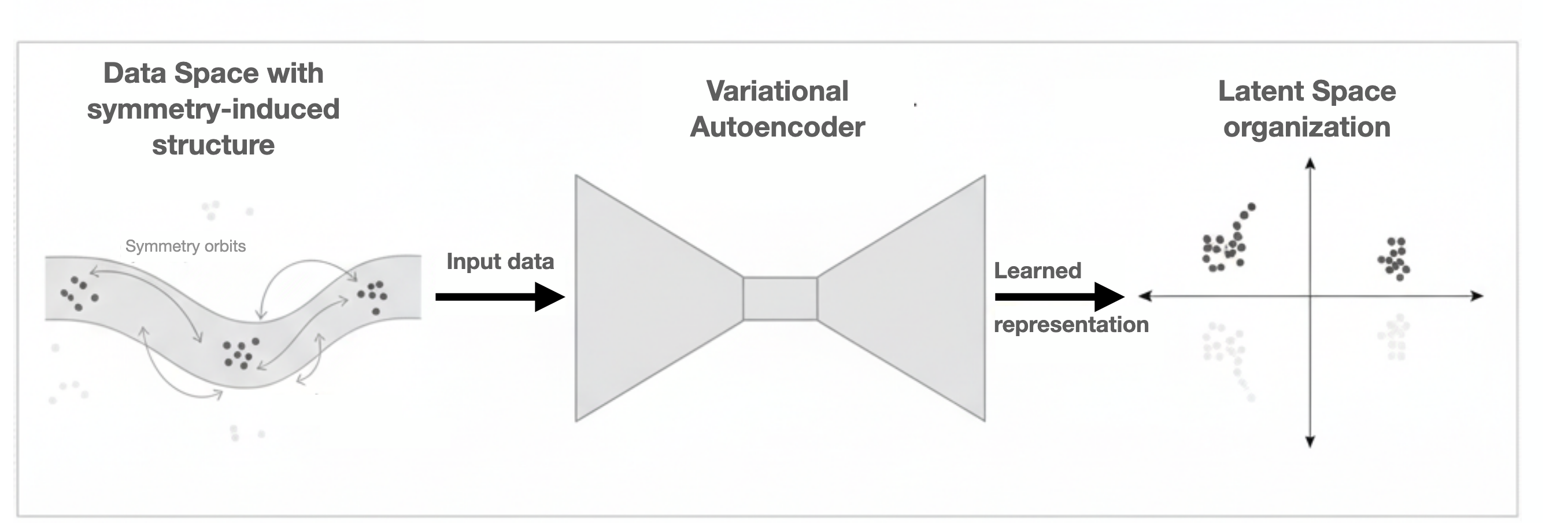
Variational autoencoders leverage symmetry-induced constraints to compress data onto a lower-dimensional manifold, prioritizing symmetry-independent latent degrees of freedom during training to balance reconstruction accuracy and efficient representation.
Variational autoencoders leverage symmetry-induced constraints to compress data onto a lower-dimensional manifold, prioritizing symmetry-independent latent degrees of freedom during training to balance reconstruction accuracy and efficient representation.

Unveiling Structure Through Generative Models

Generative models operate by learning the probabilistic distribution inherent in a training dataset. This learned distribution is then utilized to generate new data points that statistically resemble the original data. The process typically involves defining a model with parameters, estimating those parameters from the data using techniques like maximum likelihood estimation, and then sampling from the learned distribution to create new instances. The quality of generated samples is directly related to the model’s ability to accurately capture the complexities of the underlying data distribution; more sophisticated models, such as those employing deep neural networks, can often capture highly complex distributions and generate correspondingly realistic samples. This capability has applications in areas like image synthesis, text generation, and music composition, where the goal is to create new content indistinguishable from real-world examples.

Representation learning focuses on automatically discovering and extracting salient features from raw data to create condensed and informative data representations. These representations, often of lower dimensionality than the original input, are critical for effective generative modeling because they facilitate learning the underlying data distribution with fewer parameters and increased generalization ability. A well-learned representation captures the essential variations within the data, enabling generative models to synthesize new samples that are both realistic and diverse. The quality of the learned representation directly impacts the performance and efficiency of subsequent generative processes; compact representations minimize computational cost, while informative representations preserve the necessary details for high-fidelity generation.

Variational Autoencoders (VAEs) establish a probabilistic framework for learning latent representations of data. These models utilize an encoder network to map input data to a probability distribution in a latent space, and a decoder network to reconstruct the original data from samples drawn from this distribution. Our research demonstrates the utility of VAEs in identifying and organizing latent spaces to reveal underlying symmetry-induced structure within datasets. Specifically, by analyzing the organization of the latent space, we can identify dimensions that correspond to symmetries present in the data, allowing for a more interpretable and compact representation. This approach enables the discovery of inherent data characteristics without requiring explicit symmetry labels or prior knowledge.

The Information Bottleneck (IB) Principle provides a theoretical framework for learning representations that balance compactness and information retention. IB seeks to find a compressed representation [latex]Z[/latex] of input data [latex]X[/latex] that minimizes the mutual information [latex]I(X;Z)[/latex], thereby enforcing compactness, while simultaneously maximizing the mutual information between the representation [latex]Z[/latex] and a target variable [latex]Y[/latex], denoted as [latex]I(Y;Z)[/latex]. This optimization process encourages the discovery of representations that discard irrelevant information from the input while preserving information crucial for predicting the target, resulting in efficient and informative data encoding. Applying IB during representation learning compels the model to prioritize salient features and create representations that are both concise and predictive.

Analysis of hadron collision data reveals a latent relevance spectrum with a softened hierarchy, indicating approximate and kinematically dependent constraints, as detailed in Ref.Sanz (2025).
Analysis of hadron collision data reveals a latent relevance spectrum with a softened hierarchy, indicating approximate and kinematically dependent constraints, as detailed in Ref.Sanz (2025).

The Power of Symmetry in Modeling

Data augmentation, a common technique for expanding training datasets, benefits substantially when guided by an understanding of inherent symmetries within the data itself. Rather than applying random transformations, informed augmentation leverages the predictable ways in which data changes under operations like rotation, reflection, or permutation. By generating new training examples that respect these symmetries, models learn to focus on essential features, becoming less sensitive to irrelevant variations and thus improving generalization performance. This approach is particularly valuable when labeled data is scarce, as it effectively multiplies the information content of existing samples and builds robustness against noisy or incomplete inputs – ultimately leading to more reliable and efficient machine learning systems.

Equivariant Neural Networks represent a paradigm shift in neural network design by explicitly incorporating the principles of symmetry. Traditional neural networks often treat inputs as existing in isolation, failing to recognize inherent symmetries present in the data – such as an object remaining identifiable regardless of its rotation or translation. These networks, in contrast, are constructed to ensure that the network’s output transforms in a predictable way when the input undergoes a known transformation. This is achieved by designing network layers that respect these symmetries, meaning a rotation of the input will result in a corresponding rotation of the output, rather than an arbitrary change. The benefit extends beyond simply maintaining geometric relationships; it drastically reduces the number of parameters needed to learn a symmetric function, improving generalization, enhancing robustness to perturbations, and fostering a more efficient use of data – ultimately leading to models that are both more powerful and more interpretable.

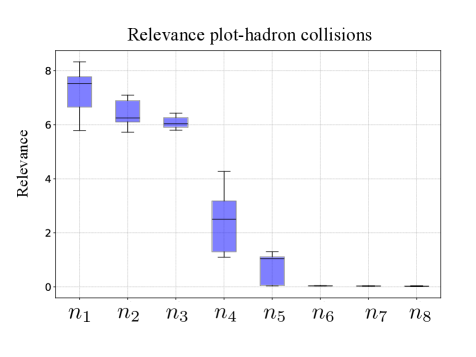
Generative models, while powerful, often rely on a high-dimensional latent space where many dimensions contribute little to the generated output. Recent research has introduced a “relevance measure” to dissect this latent space, quantifying each variable’s contribution to the reconstruction of generated data. This measure doesn’t simply identify unimportant dimensions – it reveals a hierarchical structure, demonstrating how latent variables organize themselves to control different aspects of the generated content. By pinpointing the number of effectively utilized dimensions, researchers gain insights into the model’s true capacity and can potentially reduce dimensionality without sacrificing performance, leading to more efficient and interpretable generative processes. The technique offers a pathway toward understanding how generative models represent information, moving beyond a ‘black box’ approach to a more transparent and controllable system.

The convergence of robust modeling techniques – leveraging symmetry in data augmentation and network design – yields benefits extending beyond simple predictive power. Models built with these principles demonstrate enhanced generalization capabilities, performing reliably even with noisy or incomplete data. Importantly, these approaches aren’t merely about achieving higher accuracy; they also foster interpretability, allowing researchers to understand how a model arrives at its conclusions. This increased transparency is coupled with improved computational efficiency; by exploiting inherent symmetries, these models often require fewer parameters and less training data to reach peak performance, representing a significant advancement in practical machine learning applications.

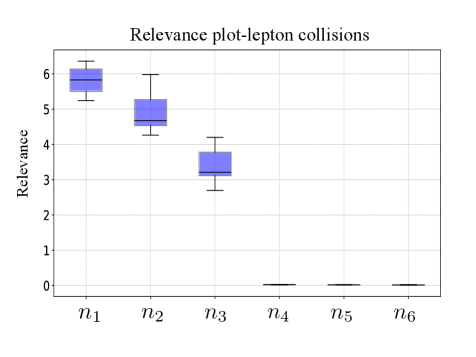
Analysis of lepton collision data reveals three dominant latent directions corresponding to the constraints imposed by momentum conservation, as demonstrated in Ref. Sanz (2025).
Analysis of lepton collision data reveals three dominant latent directions corresponding to the constraints imposed by momentum conservation, as demonstrated in Ref. Sanz (2025).

The exploration of symmetries within complex datasets, as detailed in the article, mirrors a fundamental principle of emergent order. The system reveals its underlying structure not through imposed control, but through the identification of inherent patterns-a process akin to discovering the ‘local rules’ governing a complex organism. Marie Curie observed, “Nothing in life is to be feared, it is only to be understood.” This sentiment resonates deeply with the paper’s approach; rather than attempting to dictate structure, the variational autoencoders serve as a diagnostic lens, illuminating the latent symmetries already present within the physical data. The reduction of dimensionality through latent space analysis isn’t about simplification, but about recognizing the core, organizing principles that govern the system’s behavior.

Beyond the Looking Glass

The pursuit of symmetry, as this work demonstrates, isn’t about imposing order, but about recognizing its inherent presence. The variational autoencoder, deployed as a diagnostic, merely offers a new lens through which to view data’s self-organization. The true challenge lies not in finding symmetry, but in understanding why it so readily emerges – why the universe seems predisposed to efficient encoding. This suggests a deeper principle at play, one where complexity isn’t built, but sculpted from simpler foundations.

Limitations remain, of course. Current methods struggle with symmetries that aren’t explicitly present in the training data, hinting at a need for architectures that can infer underlying structure. Furthermore, the interpretation of the latent space-that compressed representation of reality-remains a subjective exercise. A more rigorous connection to effective field theory, beyond simply mirroring its mathematical forms, is crucial. The goal shouldn’t be to replicate known physics, but to allow the data itself to suggest new theoretical frameworks.

Stability and order emerge from the bottom up; top-down control is merely an illusion of safety. Future work should focus less on building intelligent systems and more on creating environments where inherent organizational principles can flourish. The machine isn’t the architect; it’s a mirror, reflecting the universe’s own elegant self-assembly.

Original article: https://arxiv.org/pdf/2602.02351.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-02-03 13:09