Beyond Sets: Learning Continuous Representations for Discrete Data

Author: Denis Avetisyan

A new framework, CORDS, offers a powerful way to represent variable-size collections of objects using continuous fields, bridging the gap between discrete and continuous learning.

The study transforms a two-dimensional function into a density field [latex]\rho(x,y)[/latex] by treating local peaks and valleys as individual entities and encoding their relationships using the CORDS method, effectively mapping a continuous surface onto a discrete representation.

CORDS introduces a novel approach to representing discrete structures with continuous fields, achieving competitive results in areas like molecular generation and object detection.

Many machine learning tasks require predicting sets of objects with variable cardinality, presenting challenges for methods reliant on fixed-size inputs or explicit set size inference. To address this, we introduce ‘CORDS: Continuous Representations of Discrete Structures’, a novel framework that represents discrete sets as continuous fields-a density field encoding location and count, and a feature field capturing attributes. This invertible mapping allows models to operate entirely in continuous space while remaining precisely decodable to discrete sets, demonstrating robust performance across molecular generation, object detection, and simulation-based inference. Could this continuous representation paradigm unlock new capabilities for handling complex, variable-sized data in diverse scientific domains?

Deconstructing Sets: The Limits of Fixed Representation

Across diverse scientific fields, from molecular biology to social science, researchers frequently encounter data structured as sets of varying sizes. These sets – be they molecules interacting in a solution, particles detected in a physics experiment, or individuals connected within a social network – present a fundamental challenge for traditional data analysis techniques. Many established methods rely on representing data within fixed-size grids or tensors, an approach that inherently struggles with the flexibility required to efficiently handle sets containing a differing number of elements. This mismatch often necessitates padding, truncation, or other forms of data manipulation, leading to information loss and hindering the development of models capable of generalizing across datasets with varying set sizes. The inability to directly process variable-size sets limits the potential for discovering meaningful patterns and relationships within these complex systems.

A fundamental challenge in analyzing variable-size sets arises from the common practice of forcing these collections into fixed-size input formats. This process invariably results in information loss, as details specific to the set’s actual size and constituent relationships are either discarded or distorted to fit the predefined structure. Consequently, models trained on fixed-size representations struggle to generalize effectively when presented with sets differing significantly in scale or complexity from those encountered during training. The inherent limitation restricts the adaptability of these approaches, hindering their application to real-world scenarios where set sizes are rarely uniform and often crucial to meaningful analysis. This inflexibility underscores the need for methods that can inherently accommodate variable-size inputs without sacrificing critical information or predictive power.

A significant limitation of many current approaches to analyzing variable-size sets lies in their dependence on permutations – all possible orderings of the set’s elements. While permutations theoretically capture all relational information, calculating and processing them rapidly becomes computationally prohibitive as set size increases – a problem scaling factorially. More critically, this permutation-based approach treats sets as purely symbolic arrangements, effectively discarding any potential underlying geometric structure or spatial relationships that might exist between the elements. This lack of geometric awareness hinders the development of models capable of generalizing effectively to unseen data, as it fails to leverage potentially crucial information encoded in the relative positions or arrangements of set members. Consequently, researchers are actively seeking alternative methods that move beyond simple reordering to incorporate inherent structural understanding within these variable-size sets.

NNMNIST digits are encoded into a density field [latex]
ho(\mathbf{r})[/latex] and per-class feature fields [latex]h\_{k}(\mathbf{r})[/latex], with the total number of objects represented by the integral of the density field [latex]N=\in t\rho(\mathbf{r})\,d\mathbf{r}[/latex].

CORDS: A Fluid Representation for Variable Collections

CORDS represents variable-sized sets of objects by transforming discrete object data into continuous density and feature fields. This is achieved by defining each object as a point in a continuous space and then representing the set as a function that maps points in this space to a density value and a feature vector. The density field indicates the presence of an object, while the feature vector encodes its attributes. This continuous representation allows CORDS to move beyond the constraints of permutation-sensitive methods, which struggle with unordered data, and instead leverage the tools of continuous function analysis for set processing. Effectively, CORDS converts a discrete set into a continuous function [latex]f: \mathbb{R}^n \rightarrow \mathbb{R}^d[/latex], where [latex]n[/latex] represents the dimensionality of the feature space and [latex]d[/latex] represents the feature vector length.

CORDS utilizes a Temporal Backbone to sequentially process attributes associated with each object within a set; this backbone is a recurrent neural network that captures dependencies between attributes and generates a time-series representation of object characteristics. Concurrently, Channels are incorporated to encode nuanced features; each channel focuses on a specific aspect of the object’s attributes, allowing for a multi-faceted representation. These channels operate independently but contribute to a unified feature vector, enabling the network to differentiate between objects based on subtle variations in their attributes and relationships. The combined output of the Temporal Backbone and Channels provides a rich, informative representation of each object within the set, facilitating downstream tasks.

Traditional set-based methods often rely on permutation-invariant operations, requiring computation across all possible orderings of set elements – a process with factorial complexity. CORDS avoids this limitation by encoding sets as continuous fields, effectively transforming discrete set elements into values within a continuous space. This representation allows for the application of standard convolutional or other continuous function processing techniques, significantly reducing computational cost. Consequently, operations on sets are performed on these fields, enabling efficient computation regardless of set size or the number of elements, and facilitating parallelization on standard hardware.

Denoising diffusion transforms initially dispersed node feature fields [latex]\mathbf{h}_{\text{n}}(\mathbf{r})[/latex] into well-separated continuous representations that accurately encode discrete graph structure and allow for reconstruction of node positions and features.

Echoes of Physics: Borrowing from Simulation

CORDS utilizes computational techniques inspired by physics-based simulations, specifically drawing from Smoothed-Particle Hydrodynamics (SPH) and Particle-in-Cell (PIC) methods. Both SPH and PIC rely on representing a field as a continuous function derived by convolving discrete particles with smoothing kernels. These kernels define the influence of each particle on neighboring points, effectively distributing particle properties to create a smooth field representation. This approach avoids the need for explicit grid structures, offering flexibility in handling complex geometries and varying data densities. The convolution operation, typically a weighted average based on distance and kernel function, determines the value of the field at any given location.

CORDS leverages the inherent stability and computational efficiency of techniques originating in physics-based simulation, specifically those found in Smoothed-Particle Hydrodynamics (SPH) and Particle-in-Cell (PIC) methods. SPH and PIC are well-established for handling dynamic systems and field calculations by representing data as discrete particles and utilizing convolution with smoothing kernels to approximate continuous fields. By adopting this approach, CORDS minimizes common issues associated with neural field training, such as instability during optimization, and improves performance by benefiting from decades of research focused on optimizing these particle-based methods. This results in faster convergence and more robust training, particularly when dealing with complex geometric data.

CORDS leverages recent progress in Equivariant Neural Fields to improve the representation of geometric data. Prior methods, including DeepSDF, NeRF, and SIREN, have demonstrated success in implicit and neural rendering applications; however, CORDS extends these approaches by incorporating equivariance properties. This ensures that the learned neural fields transform consistently with input coordinate transformations, leading to more robust and accurate geometric representations. Specifically, CORDS builds upon these foundations to better model complex shapes and topologies, addressing limitations in earlier methods regarding generalization and detail preservation.

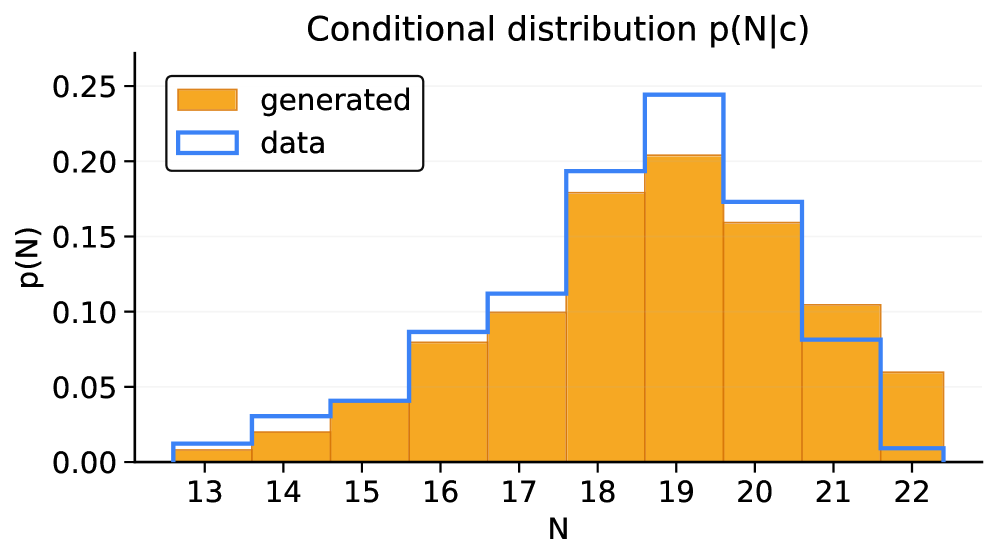
Simulation-based inference recovers light curves [latex]\ell[/latex] from posterior samples [latex]\theta \sim p(\theta \mid \ell)[/latex] by decoding sampled fields into component parameters and simulating the resulting curves, ultimately yielding a posterior distribution over the number of components [latex]p(N \mid \ell)[/latex].

Validation and Expansion: The Molecular Frontier

The CORDS framework exhibits notable efficacy in generating molecular structures, as evidenced by its performance on benchmark datasets including QM9 and GeomDrugs. Rigorous evaluation reveals that CORDS consistently surpasses the capabilities of Graph Neural Network (GNN) baselines across crucial metrics such as validity, uniqueness, and novelty of generated compounds. This improved performance isn’t simply about creating more molecules, but generating molecules with desirable characteristics and diverse structural features – a key advancement in computational chemistry and drug discovery. The method’s ability to consistently outperform established GNN approaches highlights its potential as a powerful tool for de novo molecular design and virtual screening, offering a promising pathway toward the identification of novel therapeutic candidates and materials.

A significant advantage of the CORDS methodology lies in its inherent capacity to process sets of variable size, enabling robust generalization across diverse molecular structures. Unlike many generative models constrained by fixed-length inputs, CORDS can effectively represent and generate molecules containing differing numbers of atoms – a critical capability for real-world applications where molecular complexity varies considerably. This flexibility stems from the set-based nature of the representation, allowing the model to adapt to any molecular size without requiring padding or truncation – techniques that can introduce artifacts or information loss. Consequently, the model demonstrates superior performance on datasets like QM9 and GeomDrugs, which encompass molecules with a wide range of atomic compositions, showcasing a marked improvement in its ability to extrapolate beyond the training data and accurately model unseen chemical entities.

Evaluations on standard molecular datasets reveal that CORDS attains performance competitive with, and in some cases exceeding, that of established Graph Neural Network (GNN) baselines. Specifically, when tested on the widely used `QM9` and `GeomDrugs` datasets, CORDS demonstrates a robust ability to generate valid and diverse molecular structures. Importantly, the method surpasses the performance of previously published continuous approaches specifically on the `QM9` dataset, suggesting an advancement in the field of molecular design. These results highlight CORDS’ potential as a powerful tool for both quantitative property prediction and the de novo creation of molecules with desired characteristics.

Conditional generation accurately predicts atom counts for property ranges not encountered during training, and unconditional generation on QM9, evaluated with OpenBabel postprocessing, demonstrates competitive performance against existing methods.

Beyond the Horizon: Expanding the Scope of Representation

The CORDS framework has been significantly extended through the implementation of spectral embeddings, allowing it to move beyond the limitations of traditional geometric graphs. This innovative approach transforms graph data into a spectral domain, representing nodes based on their relationships and connectivity rather than spatial coordinates. Consequently, CORDS can now be applied to a far wider range of datasets – including social networks, knowledge graphs, and even complex relational databases – where geometric interpretations are not naturally present. By focusing on the intrinsic spectral properties of these non-geometric graphs, the extension unlocks the potential for discovering patterns and relationships previously inaccessible, opening new avenues for research in diverse fields such as social science, information retrieval, and beyond.

The development of CORDS is being significantly accelerated through the integration of large language models. These models aren’t merely tools for automation; they actively participate in the coding process, generating new functionalities and refining existing code with remarkable efficiency. This approach allows researchers to rapidly prototype and test novel extensions to the framework, overcoming traditional bottlenecks in software development. Beyond simply speeding up the process, this methodology fosters innovation by enabling the exploration of a wider range of potential features and applications, effectively lowering the barrier to entry for future contributions and ensuring CORDS remains adaptable to emerging challenges in diverse scientific domains.

The continued development of CORDS is poised to address increasingly complex challenges through expansion to massive datasets. Researchers anticipate that scaling CORDS’ capabilities will unlock its potential in fields demanding sophisticated data analysis, notably robotics and computational physics. In robotics, this could facilitate more nuanced robot learning and adaptive behavior, while in computational physics, it offers a pathway toward accelerating simulations and discovering novel insights from complex physical systems. This progression necessitates not only algorithmic optimization for handling larger data volumes but also the exploration of distributed computing architectures to manage the computational demands of these advanced applications, promising a future where CORDS serves as a foundational tool for scientific discovery and technological innovation.

CORDS encodes a molecular graph into a density field [latex]
ho(\mathbf{r})[/latex] and feature fields [latex]h_{k}(\mathbf{r})[/latex] representing atom types, with the total atom count directly reflected in the integrated density [latex]K=\in t\rho(\mathbf{r})\,d\mathbf{r}[/latex].

The exploration within CORDS actively embodies a spirit of challenging established boundaries. It posits that discrete structures, traditionally handled as distinct entities, can be effectively represented through the fluidity of continuous fields. This approach isn’t merely about finding a different method; it’s about questioning the fundamental necessity of discrete categorization itself. As Henri Poincaré observed, “Pure mathematics is, in its way, the poetry of logical relations.” CORDS, in translating discrete complexities into continuous representations, demonstrates a similar elegance – a reimagining of how information is structured, and a testament to the power of reframing a problem to unlock new possibilities, particularly when dealing with variable cardinality sets and their application in areas like object detection.

Beyond the Grid: Future Exploits

The elegance of CORDS lies in its sidestepping of inherent limitations imposed by discrete representations. However, this is not a solved problem, merely a clever circumvention. The framework’s reliance on continuous fields introduces a new set of challenges – namely, the efficient encoding of truly complex relationships within those fields. Current implementations, while demonstrating competitive performance, still operate within relatively constrained search spaces. The true exploit of comprehension will come from expanding those spaces, allowing the density and feature fields to represent not just what is present, but the nuanced probabilities of what could be.

A key limitation is the implicit assumption of Euclidean space. Discrete structures rarely conform to such neat geometries. Future work must address the challenge of non-Euclidean CORDS – how to represent sets embedded in complex manifolds, or those governed by non-linear dynamics. This demands a shift in thinking, moving beyond simple coordinate-based fields towards representations that are invariant to transformations and robust to noise.

Ultimately, the success of this approach hinges on its ability to bridge the gap between continuous and discrete. The field has long treated these as opposing forces. CORDS suggests they are simply different facets of the same underlying reality. The next step is not refinement, but radical generalization – a framework that can seamlessly represent any structure, regardless of its inherent discreteness or continuity.

Original article: https://arxiv.org/pdf/2601.21583.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/