Author: Denis Avetisyan
A novel method leveraging paired autoencoders offers a powerful solution for recovering complete data from incomplete or corrupted observations.
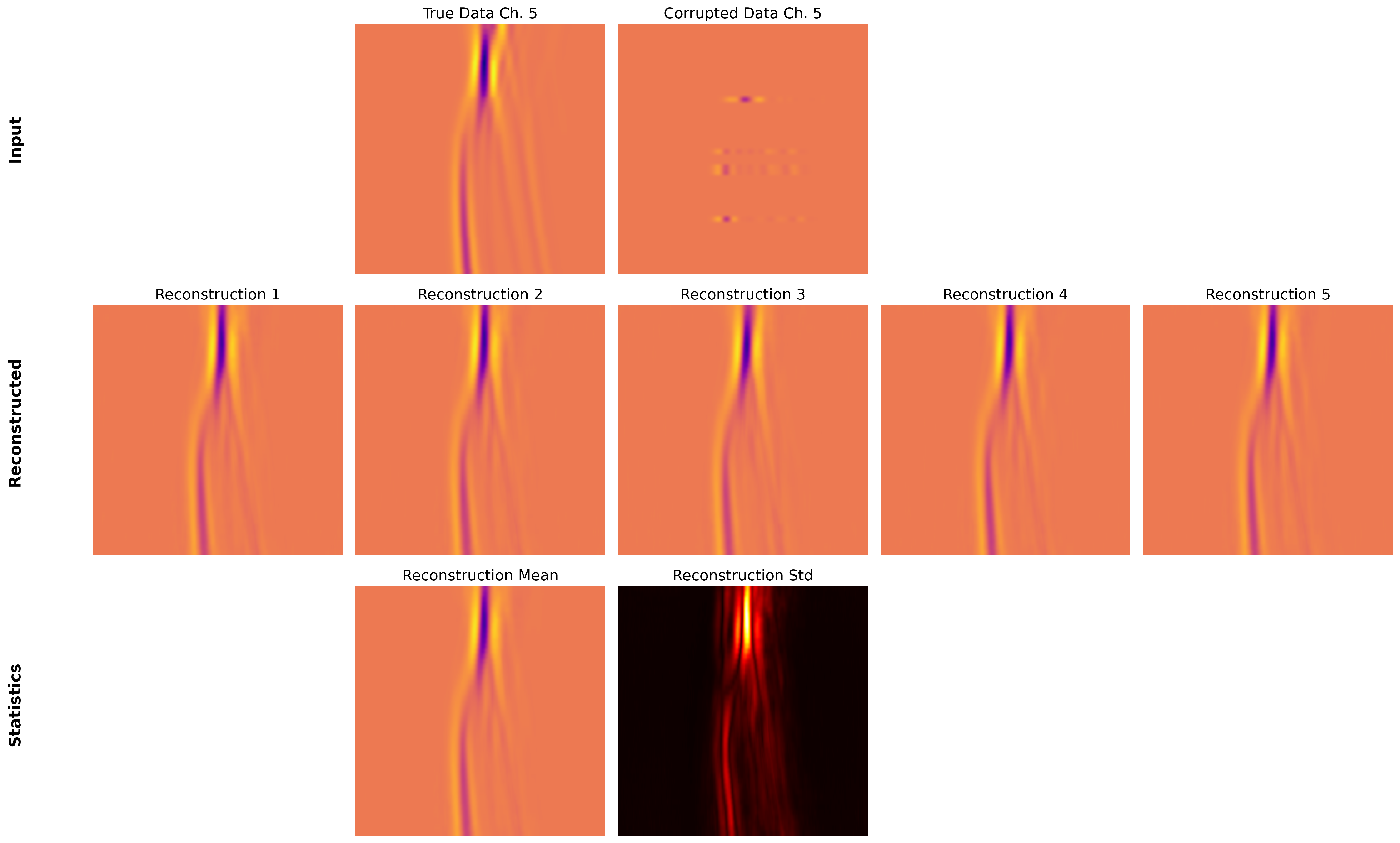
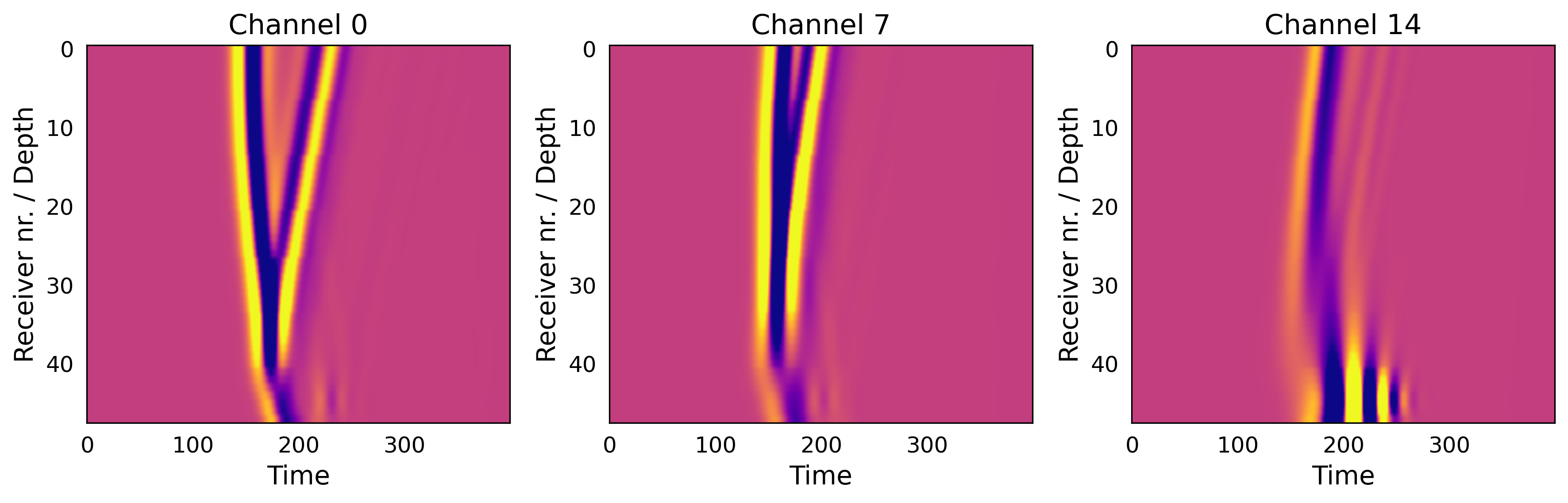
This review details a latent space inference technique utilizing paired autoencoders to address ill-posed inverse problems and enhance data reconstruction.
Inverse problems are often ill-posed, yielding unstable or non-unique solutions when reconstructing underlying parameters from incomplete or noisy observations. This work introduces a novel framework for ‘Latent Space Inference via Paired Autoencoders’ that addresses this challenge by learning consistent latent representations between parameter and observation spaces. By connecting paired autoencoders with learned mappings, we enable robust data reconstruction and improved parameter estimation, even with significant data inconsistencies. Could this approach unlock more accurate and efficient solutions for a broader range of scientific and engineering inverse problems?
Unveiling Hidden Structures: The Essence of Inverse Problems
The pursuit of understanding underlying causes from observed outcomes defines the core of inverse problems, a critical challenge across diverse scientific and engineering disciplines. From medical imaging – reconstructing internal anatomy from X-rays or MRI signals – to seismology – determining earthquake origins and Earth’s internal structure from wave propagation – and even in astronomy, where the composition of distant stars is inferred from their emitted light, these problems are ubiquitous. This approach differs fundamentally from ‘forward problems’ where causes are known and effects are predicted; instead, inverse problems require deducing the ‘source’ given the ‘result’. Consequently, they underpin technologies like signal processing, materials science, and non-destructive testing, fundamentally shaping how knowledge is gained from indirect measurements and enabling solutions where direct observation is impossible.
Inverse problems, ubiquitous across disciplines like medical imaging and geophysics, frequently exhibit a characteristic known as ill-posedness. This doesn’t imply a flaw in the underlying physics, but rather a mathematical sensitivity where small changes in observed data can lead to dramatically different, and potentially unrealistic, solutions. Unlike ‘well-posed’ problems with unique and stable answers, ill-posed problems often yield solutions that are highly unstable; they oscillate wildly or simply don’t exist at all without specific constraints. Consider attempting to reconstruct a blurry image – an infinite number of original images could produce the same blurred result. Addressing this requires carefully designed techniques, such as regularization, which introduces prior knowledge or constraints to stabilize the solution and favor physically plausible outcomes, effectively trading some accuracy for robustness and ensuring a meaningful, interpretable result.
The reliability of inferences drawn from inverse problems is frequently challenged by the pervasive presence of noise and missing data. Real-world observations are rarely perfect; sensor inaccuracies, environmental interference, and incomplete measurements introduce errors that can dramatically skew results. Consequently, researchers employ a variety of robust methods – from statistical filtering and regularization techniques to advanced machine learning algorithms – designed to mitigate these uncertainties. These approaches aim to distinguish genuine signals from spurious noise, effectively fill in gaps caused by missing data, and ultimately provide stable and meaningful solutions, even when faced with imperfect or incomplete information. The development and refinement of these techniques remain crucial for extracting accurate insights across diverse fields, including medical imaging, geophysical exploration, and signal processing.

Harnessing Data: Deep Learning as a Solution
Deep Learning provides a robust approach to solving Inverse Problems by establishing learned mappings between observed data and underlying causes or solutions. Traditional methods often rely on explicitly defined models and iterative algorithms, which can be computationally expensive and sensitive to noise. Conversely, Deep Learning models, typically employing multi-layered neural networks, learn these mappings directly from data. This data-driven approach allows the network to approximate complex, non-linear relationships that are difficult or impossible to model analytically. The efficacy of this paradigm stems from the network’s ability to generalize from training data to unseen observations, effectively reconstructing solutions to inverse problems even with incomplete or noisy inputs. This is particularly useful in scenarios where a forward model is either unknown or computationally intractable.
Deep learning’s capacity for solving complex problems relies fundamentally on its utilization of neural network architectures, with autoencoder models being particularly prominent in representation learning. Autoencoders function by learning a compressed, latent-space representation – or encoding – of input data, and then reconstructing the original input from this compressed form. This process forces the network to learn the most salient features of the data, effectively extracting meaningful representations that capture essential information while discarding noise or redundancy. The resulting latent space allows for dimensionality reduction, data denoising, and the identification of underlying patterns, providing a robust foundation for downstream tasks such as classification, regression, or anomaly detection. Different autoencoder variants, including sparse, variational, and denoising autoencoders, offer variations on this core principle to optimize representation learning for specific applications.
End-to-end inference in deep learning streamlines the solution process by enabling the neural network to learn the complete mapping from input data to desired output without requiring hand-engineered intermediate steps or explicit formulation of the underlying physical model. Traditional approaches often necessitate defining specific algorithms for feature extraction, data association, and solution reconstruction; however, end-to-end systems learn these transformations directly from data. This direct learning approach minimizes the need for domain expertise in problem formulation and allows the network to optimize all parameters simultaneously, potentially leading to improved performance and reduced computational cost. The network effectively learns a composite function that encapsulates all necessary processing stages, represented mathematically as y = f(x; \theta) , where x is the input, y is the output, and θ represents the network’s trainable parameters.

A Novel Architecture: Paired Autoencoders for Enhanced Stability
Paired Autoencoder frameworks address stability concerns in model learning by establishing direct, learned mappings between observable data in the observation space and the parameters defining a model. This bidirectional mapping-from observation to parameters and vice versa-constrains the parameter space during training, preventing parameter drift and promoting convergence. Unlike traditional autoencoders that focus solely on reconstructing inputs, Paired Autoencoders explicitly learn how changes in the observation space correlate to specific adjustments in the model’s parameters. This pairing enables more robust learning, particularly in scenarios with noisy or incomplete data, as the learned mapping provides a consistent and predictable relationship between observations and model state. The framework effectively regularizes the learning process by enforcing a structured relationship, thereby enhancing the overall stability of the learned model.
Latent Space Inference within the Paired Autoencoder architecture facilitates both efficient data reconstruction and the quantification of uncertainty associated with that reconstruction. By mapping input observations to a lower-dimensional latent space, the model reduces computational demands during the reconstruction process. Furthermore, analyzing the distribution of latent variables allows for the estimation of prediction uncertainty; wider distributions indicate greater uncertainty, while narrower distributions suggest higher confidence in the reconstructed output. This capability is achieved by propagating probabilistic information through the latent space, enabling the model to not only predict a single solution but also to provide a measure of its reliability, crucial for applications requiring risk assessment or decision-making under uncertainty.
Variational Autoencoders (VAEs) enhance latent space representation by introducing a probabilistic approach to encoding. Instead of mapping input data to a single point in the latent space, VAEs learn a distribution – typically a Gaussian distribution – parameterized by a mean and variance. This allows the model to represent uncertainty and generate diverse outputs by sampling from this distribution. During training, the Kullback-Leibler divergence D_{KL}(q(z|x) || p(z)) is minimized, encouraging the learned latent distribution q(z|x) to be close to a prior distribution p(z), often a standard normal distribution. This regularization promotes a well-behaved and continuous latent space, enabling more robust reconstruction and generation capabilities compared to standard autoencoders.
Impact and Applications: From Healthcare to Resource Exploration
The developed methodology finds immediate application in computed tomography (CT) imaging, a cornerstone of modern medical diagnostics. By accelerating the reconstruction process – the transformation of raw data into a visual image – clinicians can significantly reduce scan times, minimizing patient exposure to radiation while simultaneously enhancing image clarity. This improved speed and accuracy are particularly critical in emergency situations, where rapid diagnosis is paramount, and in applications requiring detailed visualization of subtle anatomical features. Furthermore, the technique’s robustness in handling incomplete or noisy data allows for more reliable diagnoses, even when imaging conditions are suboptimal, ultimately contributing to improved patient outcomes and a more efficient healthcare system.
Seismic inversion, a critical process in uncovering hidden geological structures, experiences a significant boost through this novel approach, yielding more reliable subsurface images for resource exploration. Traditional methods often struggle with noisy or incomplete data, leading to ambiguous results and hindering accurate assessments of potential oil, gas, or mineral deposits. This enhanced robustness allows for clearer delineation of subsurface layers, even in complex geological settings, by effectively mitigating the impact of data imperfections. Consequently, exploration teams can make more informed decisions regarding drilling locations and resource extraction strategies, reducing risks and maximizing efficiency in the pursuit of vital energy and material resources. The resulting improvements extend beyond mere image clarity, contributing to a more sustainable and cost-effective approach to resource management.
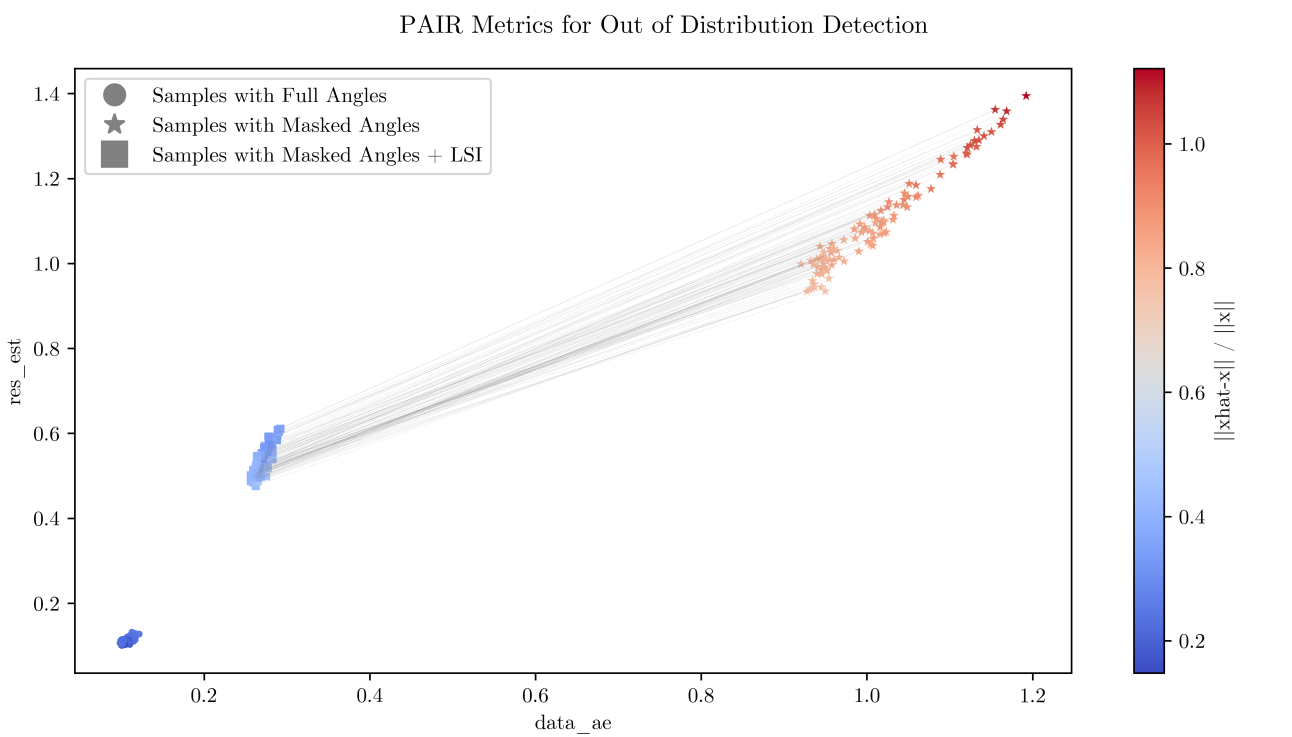
Beyond simply reconstructing a solution to an inverse problem, this methodology crucially incorporates statistical methods to rigorously quantify the inherent uncertainty within those reconstructions. This isn’t merely about obtaining an answer, but about providing a reliable estimate accompanied by a clear understanding of its limitations. By leveraging techniques like Bayesian inference and ensemble methods, the approach generates not a single value, but a probability distribution reflecting the range of plausible solutions. This allows for more informed decision-making, particularly in sensitive applications where understanding the confidence level of a result is paramount; for example, assessing the statistical significance of features identified in medical imaging or accurately evaluating resource quantities in subsurface exploration. The inclusion of uncertainty quantification transforms the reconstructed solution from a potentially misleading absolute value into a robust, statistically-grounded estimate, bolstering the overall reliability and practical utility of the findings.
The pursuit of robust data reconstruction, as detailed in this work on paired autoencoders, echoes a fundamental principle of systemic integrity. The paper elegantly addresses the challenges inherent in inverse problems – a form of ill-posedness demanding creative solutions. This mirrors the idea that a system’s overall behavior is dictated by its structure; a flawed reconstruction, much like a weakened component, compromises the whole. As John von Neumann observed, “In any investigation of this kind, it is essential to start with a clear definition of the terms.” This clarity, applied to the latent space and reconstruction process, underpins the method’s effectiveness and contributes to a more resilient solution for incomplete data.
Where Do We Go From Here?
The pursuit of solutions to ill-posed problems invariably reveals the boundaries of what can be reliably known. This work, utilizing paired autoencoders for latent space inference, offers a compelling method for data reconstruction, but it does not erase the fundamental truth: reconstruction is interpretation. The elegance of inferring structure from incomplete data relies on assumptions baked into the autoencoder architecture, and those assumptions, however cleverly designed, represent a prior belief about the underlying data generating process. The system will break along the line where that belief fails to hold.
Future work must address the question of robustness. How does this method respond to deviations from the training distribution? Can the latent space be made more resilient to noise and adversarial perturbations? More importantly, research should move beyond simply improving reconstruction fidelity and focus on quantifying the uncertainty inherent in the inference process. A perfect reconstruction is often less valuable than a faithful representation of what remains unknown.
Ultimately, the success of latent space inference will depend not on building ever-more-complex architectures, but on developing a deeper understanding of the information bottleneck. The true power lies not in squeezing data into a lower-dimensional space, but in identifying which information is truly essential, and which can be discarded without sacrificing the integrity of the system. The next generation of autoencoders will be judged not by what they can reconstruct, but by what they choose to forget.
Original article: https://arxiv.org/pdf/2601.11397.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Clash Royale Best Boss Bandit Champion decks
- Vampire’s Fall 2 redeem codes and how to use them (June 2025)
- Best Arena 9 Decks in Clast Royale
- Country star who vanished from the spotlight 25 years ago resurfaces with viral Jessie James Decker duet
- World Eternal Online promo codes and how to use them (September 2025)
- JJK’s Worst Character Already Created 2026’s Most Viral Anime Moment, & McDonald’s Is Cashing In
- ‘SNL’ host Finn Wolfhard has a ‘Stranger Things’ reunion and spoofs ‘Heated Rivalry’
- M7 Pass Event Guide: All you need to know
- Solo Leveling Season 3 release date and details: “It may continue or it may not. Personally, I really hope that it does.”
- Kingdoms of Desire turns the Three Kingdoms era into an idle RPG power fantasy, now globally available
2026-01-20 20:44