Author: Denis Avetisyan
A new framework combines boundary integral methods and machine learning to efficiently solve linear elliptic partial differential equations.
This work introduces MAD-BNO, a neural operator learning approach leveraging artificial data generated from fundamental solutions to improve accuracy and reduce computational cost for boundary integral equation solvers.
Traditional approaches to solving partial differential equations often require extensive sampling of the solution domain, presenting a computational bottleneck. This work, ‘Operator learning on domain boundary through combining fundamental solution-based artificial data and boundary integral techniques’, introduces a novel framework, MAD-BNO, that learns mappings directly from boundary data using mathematically generated artificial data and boundary integral representations. By circumventing full-domain sampling, MAD-BNO achieves accuracy comparable to existing neural operator methods while significantly reducing training time for elliptic problems like Laplace, Poisson, and Helmholtz equations. Could this boundary-focused approach unlock scalable and efficient PDE solvers for complex, three-dimensional geometries and diverse boundary conditions?
The Inevitable Bottleneck: Why PDEs Resist Simple Solutions
The behavior of the physical world, from the flow of air over an aircraft wing to the propagation of electromagnetic waves, is often governed by partial differential equations PDEs. These equations, however, present a significant challenge when seeking precise solutions, particularly when dealing with irregular shapes or systems with many interacting variables. Traditional numerical methods, while capable of approximating solutions, frequently encounter limitations when confronted with complex geometries or high-dimensional spaces. The computational cost increases dramatically, and the accuracy of the approximation can suffer, hindering progress in fields reliant on precise modeling-necessitating the development of innovative computational strategies to overcome these persistent obstacles in simulating reality.
Discretization methods, a cornerstone of numerical PDE solving, approximate continuous functions with discrete values at specific points – a process that, while enabling computation, inherently introduces both computational cost and error. The expense arises from the need for increasingly fine discretizations – more points – to accurately represent complex phenomena, particularly in higher dimensions; the number of calculations often scales exponentially with dimensionality. Simultaneously, these approximations can lead to significant errors, manifesting as inaccuracies in the solution or even numerical instability. The coarser the discretization, the faster the computation, but the larger the error; a trade-off that necessitates careful consideration of mesh refinement strategies and higher-order approximation schemes to balance efficiency and precision. This limitation drives ongoing research into adaptive methods that dynamically refine the discretization where needed, and alternative approaches that circumvent discretization altogether.
Progress across diverse scientific and engineering disciplines is fundamentally linked to the ability to accurately and efficiently solve partial differential equations. In fluid dynamics, these solvers enable the design of more aerodynamic vehicles and the prediction of weather patterns with greater precision. Electromagnetics relies on them for innovations in antenna design, wireless communication, and the development of advanced medical imaging techniques. Furthermore, structural mechanics utilizes these computational tools to create safer and more resilient buildings, bridges, and other critical infrastructure. Consequently, improvements in PDE solving algorithms directly translate into tangible advancements, pushing the boundaries of what’s possible in these fields and beyond – from optimizing energy efficiency to facilitating breakthroughs in materials science.
Beyond Discretization: Learning the Solution Landscape
Traditional methods for solving partial differential equations (PDEs) rely on discretization techniques – such as finite differences, finite elements, or spectral methods – to approximate solutions on a grid or basis. Neural Operators offer a fundamentally different approach by learning the mapping between function spaces directly, circumventing the need for explicit discretization. Instead of predicting solutions at discrete points, these models learn to approximate the infinite-dimensional solution operator \mathcal{S} that maps input functions u to output functions f , represented as f = \mathcal{S}(u) . This allows for continuous solution fields and, crucially, the ability to predict solutions for new input conditions without requiring retraining on new discrete datasets, representing a significant shift in computational PDE solving.
Neural operator models function by learning an approximation of the true solution operator, denoted as \mathcal{S}, which maps input functions u to output functions v, such that v = \mathcal{S}(u). This learned mapping allows for prediction of solutions for novel input functions without requiring additional training. Traditional methods necessitate re-solving the partial differential equation (PDE) for each new input condition, while neural operators generalize to unseen inputs by virtue of learning the underlying functional relationship. This capability is achieved through architectures designed to operate directly on function spaces, enabling the model to infer solutions for inputs not encountered during the training phase, effectively decoupling the solution process from specific discretization schemes.
DeepONet, introduced by Lu et al., establishes a core framework for neural operators by employing a branch network to encode input functions and a trunk network to decode into output functions; however, its computational complexity scales with the resolution of the input and output discretizations, limiting its efficiency for high-dimensional problems. Subsequent research has focused on addressing these limitations through modifications to the architecture, such as Fourier Neural Operators which leverage spectral representations to reduce computational cost, and MeshCNN, which applies convolutional operations directly on irregular mesh data. These alternative approaches aim to improve both the accuracy and scalability of neural operators beyond the original DeepONet formulation, particularly for problems requiring real-time predictions or handling complex geometries.
Physics-Informed Neural Networks (PINNs) represent a distinct approach to solving partial differential equations (PDEs) by integrating the governing equations directly into the neural network’s loss function. Unlike traditional methods requiring discrete datasets for training, PINNs utilize automatic differentiation to compute derivatives of the network’s output with respect to its inputs, enabling the calculation of the PDE residual at any point within the domain. This residual, representing the error in satisfying the PDE, is then added to the loss function alongside traditional data-driven loss terms, effectively enforcing the physical laws during training. The resulting network learns a solution that simultaneously minimizes data mismatch and satisfies the PDE, often requiring fewer labeled data points than conventional machine learning methods. The loss function typically takes the form \mathcal{L} = \mathcal{L}_{data} + \lambda \mathcal{L}_{PDE} , where λ is a weighting factor controlling the influence of the PDE constraint.
Reducing the Domain: A Hybrid Approach to Efficiency
The MAD-BNO framework utilizes Boundary Integral Equations (BIEs) as a core component to diminish the computational domain required for solving Partial Differential Equations (PDEs). Traditional PDE solvers discretize the entire problem domain, leading to a computational cost that scales with the volume or area of the domain. In contrast, BIEs reformulate the PDE into an integral equation defined only on the boundary of the domain. This reduction in dimensionality is significant; a 2D problem is reduced to a 1D boundary curve, and a 3D problem to a 2D surface. Consequently, computational effort and memory requirements are substantially decreased, as calculations are concentrated exclusively on representing and discretizing the boundary geometry, rather than the entire interior domain. This approach is particularly beneficial for problems with complex geometries or infinite domains where domain discretization becomes prohibitively expensive.
The MAD-BNO framework utilizes Boundary Integral Equations (BIEs) in conjunction with fundamental solutions to efficiently solve partial differential equations (PDEs) within complex geometries. Fundamental solutions, which represent the response to a point source, allow the PDE to be recast as a surface integral over the boundary of the domain, effectively reducing the computational dimensionality. This approach circumvents the need for volumetric discretization typically required by finite element or finite difference methods. Consequently, the solution is constructed directly from boundary data, minimizing computational cost and enabling accurate representation of complex domain shapes without extensive mesh refinement. The integral equation is then solved using established numerical techniques, leading to a computationally efficient method for constructing solutions in scenarios with intricate geometries and boundary conditions.
Neural Operators are integrated into the MAD-BNO framework to improve the representation of complex problem characteristics. Specifically, these operators function as learnable mappings between boundary data – encompassing both boundary conditions and source terms – and the solution operator. This allows the model to learn and generalize across a range of scenarios without requiring explicit specification of these terms. The Neural Operator effectively learns a function \mathcal{N}: X \rightarrow Y , where X represents the space of boundary data and Y represents the solution operator, enabling accurate and adaptable solutions for problems with intricate or unknown boundary characteristics. This learned representation complements the physics-based foundation of the Boundary Integral Equation method, resulting in increased solution accuracy and robustness.
Benchmarking demonstrates that the MAD-BNO framework achieves training speedups of 1 to 2 orders of magnitude when compared to current state-of-the-art methods, specifically PI-DeepONet. This acceleration is observed while maintaining a comparable level of solution accuracy, as verified through quantitative error analysis on a suite of benchmark problems. The performance gain stems from the dimensionality reduction inherent in the Boundary Integral Equation formulation, coupled with the efficient learning capabilities of the integrated Neural Operator. This allows for faster convergence during training, reducing computational costs without sacrificing solution quality.
The Fast Multipole Method (FMM) is integral to the scalability of MAD-BNO by reducing the computational complexity of evaluating the integral operators inherent in Boundary Integral Equation (BIE) formulations. Direct evaluation of these operators scales as O(N^2), where N represents the number of boundary elements. FMM approximates interactions between distant parts of the boundary with a controlled level of accuracy, reducing this complexity to O(N \log N) or even O(N) for certain problem configurations. This acceleration is crucial for handling high-dimensional problems and large-scale simulations within the MAD-BNO framework, enabling efficient computation of solutions for complex geometries and boundary conditions that would be intractable with direct evaluation methods.
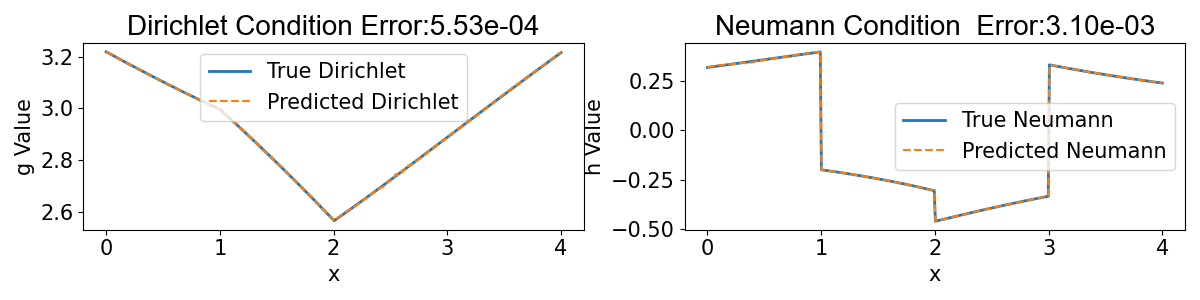
![MAD-BNO accurately predicts the analytical solution <span class="katex-eq" data-katex-display="false">m{u(x,y) = \sin(60x) \sin(80y)} </span> to the Helmholtz equation with <span class="katex-eq" data-katex-display="false"> k=100 </span>, as demonstrated by the close agreement between predicted and exact Neumann boundary values on the domain [0, 4].](https://arxiv.org/html/2601.11222v1/LN1.png)
Beyond Current Limits: Towards a More Adaptive Solver
The MAD-BNO framework demonstrates a robust capacity for managing diverse boundary conditions, crucially including both Dirichlet and Neumann types. This capability significantly expands the range of physical problems amenable to solution; Dirichlet conditions, which specify the value of a function on the boundary, are vital for modeling constrained systems, while Neumann conditions, defining the derivative across a boundary, accurately represent phenomena like heat flux or fluid flow. By effectively incorporating these conditions, MAD-BNO moves beyond simplified scenarios, offering accurate simulations of more complex, realistic physics-from electromagnetic wave propagation within defined spaces to the modeling of fluid dynamics around intricate geometries. The framework’s flexibility in handling these essential mathematical constraints establishes it as a versatile tool for a broad spectrum of scientific and engineering applications.
The MAD-BNO framework distinguishes itself through its capacity to infer complex boundary conditions directly from observational data, a capability with significant implications for traditionally challenging inverse problems. Instead of requiring explicitly defined conditions – often a major source of error or simplification – the system learns these constraints from the data itself, effectively reversing the typical PDE solving process. This data-driven approach not only circumvents the need for precise prior knowledge of boundary characteristics, but also opens avenues for parameter estimation within the governing equations. Researchers can now leverage observed system behavior to deduce previously unknown properties or refine existing models, particularly in scenarios where defining accurate boundary conditions is intractable or impossible – such as modeling subsurface flows or biological systems – fundamentally shifting the paradigm of PDE-based modeling and analysis.
A significant achievement of the MAD-BNO framework lies in its demonstrated scalability to three-dimensional problems without sacrificing accuracy. While many numerical methods experience performance degradation or require substantial computational overhead when extending from two to three dimensions, MAD-BNO maintains comparable solution fidelity in both 2D and 3D scenarios. This robustness stems from the method’s inherent design, which efficiently manages the increased complexity of higher-dimensional spaces. Consequently, researchers can confidently apply MAD-BNO to a wider range of realistic physical simulations – from fluid dynamics and heat transfer to structural mechanics – without being hampered by the computational burdens often associated with three-dimensional modeling. This scalability represents a crucial step toward practical applications and broad adoption of the framework.
Investigations are now directed toward adapting the MAD-BNO framework to address time-dependent partial differential equations, a significant expansion beyond its current steady-state capabilities. This progression necessitates tackling the complexities of temporal discretization and ensuring stability across varying time scales. Simultaneously, research is underway to explore the application of MAD-BNO to multi-physics simulations, where the interplay of different physical phenomena-such as fluid dynamics with heat transfer or electromagnetism-requires solving coupled PDEs. Successfully integrating MAD-BNO into these complex simulations promises a powerful tool for modeling intricate real-world systems and opens avenues for investigating emergent behaviors arising from the interaction of multiple physical processes. This expansion anticipates a versatile solver capable of handling a broader spectrum of scientific and engineering challenges.
The development of this methodology signifies a substantial leap towards a new era of partial differential equation (PDE) solvers. Current numerical methods often struggle with the intricacies of real-world applications, demanding extensive manual tuning and simplification of complex geometries or boundary conditions. This research demonstrates a pathway beyond these limitations, presenting a framework capable of learning directly from data and adapting to previously intractable problems. The resulting solvers promise not only enhanced accuracy and computational efficiency, but also a remarkable flexibility – allowing researchers and engineers to model increasingly sophisticated phenomena with greater confidence and reduced computational cost. Ultimately, this work positions the field to tackle previously insurmountable challenges in areas ranging from fluid dynamics and heat transfer to materials science and beyond, fostering innovation across diverse scientific and engineering disciplines.
![MAD-BNO accurately predicts the analytical solution <span class="katex-eq" data-katex-display="false"> \bm{u(x,y) = \sin(60x) \sin(80y)} </span> of the Helmholtz equation with <span class="katex-eq" data-katex-display="false"> k=100 </span>, as demonstrated by the close agreement between predicted and exact Neumann boundary values on the domain [0, 4].](https://arxiv.org/html/2601.11222v1/H10000N.png)
The pursuit of a perfectly predictive model, as explored in this work with MAD-BNO and its refinement of boundary integral techniques, echoes a fundamental truth about all systems. It is not about achieving flawless execution, but about embracing the inevitable imperfections that allow for adaptation and growth. As Carl Friedrich Gauss observed, “Errors are inevitable; it is how we correct them that defines us.” This research, by strategically introducing artificial data, doesn’t aim to eliminate error in PDE solving – a futile endeavor – but rather to guide the learning process, anticipating and accommodating limitations. A system that never breaks is, indeed, a dead one; this framework acknowledges that and builds resilience through controlled imperfection.
What Lies Ahead?
The pursuit of efficient PDE solvers, as exemplified by this work, often feels less like engineering and more like rearranging deck chairs. The elegance of boundary integral formulations, combined with the promise of operator learning, merely shifts the locus of future fragility. Scalability is, after all, just the word used to justify complexity. A framework that thrives on artificially generated data implicitly acknowledges the limitations of truly representative datasets, and therefore, the inevitable drift between training and deployment realities.
The real challenge isn’t achieving faster solutions for known equations, but building systems resilient to the unknown. Each architectural choice, each optimization for current performance, is a prophecy of future inflexibility. The creation of a perfectly general PDE solver remains a myth-a comforting fiction to sustain the effort. The next phase will likely see a move beyond simply learning solutions, towards systems that learn to adapt to novel problem structures, potentially through meta-learning or intrinsically motivated exploration of the solution space.
One anticipates a growing recognition that the boundaries of the domain are not merely geometric constraints, but the very limits of the model’s understanding. The focus will shift from minimizing error on benchmarks, to maximizing robustness in the face of unforeseen conditions. Ultimately, the success of these methods will be judged not by their speed, but by their capacity to gracefully degrade as the underlying assumptions inevitably fail.
Original article: https://arxiv.org/pdf/2601.11222.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Clash Royale Best Boss Bandit Champion decks
- Vampire’s Fall 2 redeem codes and how to use them (June 2025)
- Best Arena 9 Decks in Clast Royale
- World Eternal Online promo codes and how to use them (September 2025)
- Country star who vanished from the spotlight 25 years ago resurfaces with viral Jessie James Decker duet
- ‘SNL’ host Finn Wolfhard has a ‘Stranger Things’ reunion and spoofs ‘Heated Rivalry’
- JJK’s Worst Character Already Created 2026’s Most Viral Anime Moment, & McDonald’s Is Cashing In
- Solo Leveling Season 3 release date and details: “It may continue or it may not. Personally, I really hope that it does.”
- Kingdoms of Desire turns the Three Kingdoms era into an idle RPG power fantasy, now globally available
- M7 Pass Event Guide: All you need to know
2026-01-20 13:15