Beyond Well-Behaved Cells: Challenging Assumptions in Cylindrical Algebraic Decomposition

Author: Denis Avetisyan

A new analysis reveals that commonly held beliefs about the topological properties of cells within cylindrical algebraic decompositions do not always hold true, even in relatively simple cases.

The cornet cell <span class="katex-eq" data-katex-display="false">\mathfrak{C}</span> and the slit disk <span class="katex-eq" data-katex-display="false">\mathbb{D}_{\text{s}}</span> are delineated by dashed boundaries, establishing a geometric relationship critical to their respective definitions. — The cornet cell $\mathfrak{C}$ and the slit disk $\mathbb{D}_{\text{s}}$ are delineated by dashed boundaries, establishing a geometric relationship critical to their respective definitions.

This paper presents explicit counterexamples in ℝ⁴ demonstrating failures of contractibility of closures and regularity of sectors for certain CAD cells, disproving previously stated conjectures.

While Cylindrical Algebraic Decompositions (CADs) are foundational to both symbolic computation and the study of semi-algebraic sets, assumptions regarding their topological properties have remained largely unproven. This paper, ‘On some Exotic Cylindrical Algebraic Decompositions and Cells’, constructs explicit counterexamples in ℝ⁴ demonstrating that key topological characteristics-such as contractibility of cell closures and regularity of sectors-do not universally hold for CAD decompositions. These findings refute several long-standing conjectures posed by Davenport, Locatelli, and Sankaran regarding CADs and their topological implications. Do these results necessitate a reevaluation of the implicit assumptions underlying applications of CADs in fields like robotics and geometric modeling?

Decompositional Integrity: The Foundation of Geometric Systems

The resolution of numerous geometric problems necessitates the division of complex spaces into more manageable, simpler cells – a process akin to breaking down a complicated puzzle into individual pieces. However, simply dividing a space isn’t sufficient; the resulting decomposition must be ‘well-behaved’ to guarantee a solvable outcome. This means the cells must combine in a predictable and complete manner, avoiding ambiguities or gaps that would render subsequent calculations unreliable. Without these qualities, algorithms designed to analyze or manipulate the space can become trapped in infinite loops or produce incorrect results. Ensuring this structural integrity is, therefore, paramount to the success of any geometric computation, influencing everything from collision detection in robotics to the verification of geometric models in computer-aided design.

The utility of decomposing a geometric space into simpler cells – a common strategy for tackling complex problems – rests heavily on the characteristics of that decomposition; specifically, properties like closure-finiteness and well-borderedness are paramount. Closure-finiteness ensures that the intersection of the decomposition’s cells with any algebraic variety results in a finite number of cells, preventing infinite loops in computational processes. Well-borderedness, meanwhile, guarantees that cells meet in a controlled and predictable manner – their boundaries align neatly, simplifying calculations and preventing ambiguities when analyzing relationships between them. Without these properties, a decomposition, however elegant in theory, can become computationally intractable, hindering its practical application in fields ranging from robotics and computer-aided design to algebraic geometry and real algebraic computation. These characteristics essentially provide a level of ‘robustness’ to the decomposition, ensuring reliable and efficient performance.

Cylindrical Algebraic Decomposition (CAD) stands as a cornerstone technique in computational geometry and real algebra, enabling the rigorous solution of complex problems involving systems of polynomial equations and inequalities. However, the potency of CAD isn’t inherent; it fundamentally depends on the ‘well-behaved’ nature of the underlying decomposition. Specifically, properties such as closure-finiteness – ensuring a limited number of cells at each level of refinement – and well-borderedness – guaranteeing cells are delineated by algebraic surfaces – are critical for achieving termination and generating a practical, usable decomposition. Without these foundational qualities, the process can become computationally intractable, producing infinite or excessively complex results, and undermining the method’s ability to reliably analyze geometric and algebraic spaces. Thus, ensuring these properties are met is not merely a technical detail, but a prerequisite for the successful application of CAD.

Sectoral Analysis: Defining Localized Topological Characteristics

A sector, in the context of decomposition analysis, defines a localized region of a mathematical space that is delimited by a set of defining functions. These functions serve as boundaries, effectively creating a bounded region for focused investigation. The size and shape of a sector are determined by the specific functions used in its construction, and multiple sectors are typically used to decompose a larger, more complex space. Analyzing the behavior within each sector-rather than the entire space at once-simplifies the problem by allowing for localized assessments of properties like continuity, differentiability, and convergence. This decomposition facilitates the application of analytical techniques to individual sectors, enabling a more manageable and precise understanding of the overall system’s behavior.

Equiregularity, in the context of sector decomposition, assesses whether the local behavior of a sector is topologically equivalent to that of an open ball. This equivalence is formally determined through a ‘Homeomorphism of Pairs’, which requires a continuous, bijective mapping between the sector and the open ball, preserving the structure of both the sector’s bounding functions and its interior. Specifically, the mapping must be a homeomorphism – continuous in both directions – and must map the bounding functions of the sector to the boundary of the open ball. Sectors exhibiting equiregularity allow for the application of standard analytical techniques due to this predictable topological structure; deviations from equiregularity indicate more complex behavior requiring alternative analytical approaches.

Non-equiregular sectors, those lacking a Homeomorphism of Pairs to an open ball, necessitate adjustments to standard analytical methods. Techniques relying on local Euclidean approximations, such as those employed in manifold theory or differential equations, may yield inaccurate or invalid results when applied to these sectors. The deviation from equiregularity introduces singularities or non-smooth behavior that disrupts the assumptions underlying these techniques; specifically, properties like uniform continuity or the existence of well-defined derivatives may no longer hold. Consequently, analysis within non-equiregular sectors often requires the implementation of specialized techniques designed to address these specific irregularities, potentially involving rescaling, approximation with piecewise-smooth functions, or the use of generalized derivatives.

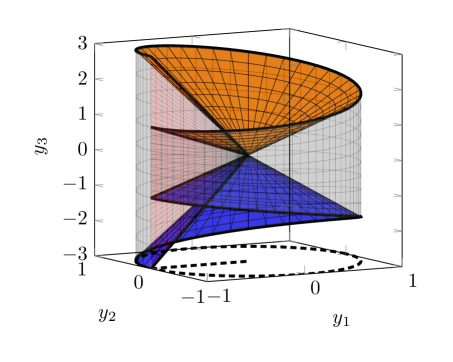
The diagram illustrates the domains <span class="katex-eq" data-katex-display="false">\mathbb{D}_{\text{s}}\odot\{-\widetilde{u}\}</span> (blue) and <span class="katex-eq" data-katex-display="false">\mathbb{D}_{\text{s}}\odot\{\widetilde{u}\}</span> (orange), their boundaries, and the sector <span class="katex-eq" data-katex-display="false">\mathbb{D}_{\text{s}}\odot(-\widetilde{u},\widetilde{u})</span> (gray) as defined in Proposition 3.12, with the red sector shown as a subset of the sector’s closure. — The diagram illustrates the domains $\mathbb{D}_{\text{s}}\odot\{-\widetilde{u}\}$ (blue) and $\mathbb{D}_{\text{s}}\odot\{\widetilde{u}\}$ (orange), their boundaries, and the sector $\mathbb{D}_{\text{s}}\odot(-\widetilde{u},\widetilde{u})$ (gray) as defined in Proposition 3.12, with the red sector shown as a subset of the sector’s closure.

Constructing the Counterexample: The Cornet Cell and Sectoral Irregularities

The Cornet Cell is a canonically defined CAD (Constructive Algebraically Defined) cell in $ℝ⁴$ utilized as a foundational element in the construction of counterexamples to several conjectures in geometric model theory. Its precise definition involves a specific arrangement of algebraic cylinders and planes, creating a bounded cell with a non-trivial boundary. This cell isn’t simply a geometric shape; it’s engineered with properties that, when combined with other CAD objects like the Slit Disk, demonstrably violate criteria for regularity. The Cornet Cell’s construction is critical because it provides a concrete, verifiable starting point for building sectors that disprove claims regarding closure-finiteness, well-borderedness, and overall regularity of CAD decompositions.

The combination of the Cornet Cell and the Slit Disk provides a mechanism for generating sectors that violate the equiregularity test. The Cornet Cell establishes a foundational geometry, while the introduction of the Slit Disk creates a specific discontinuity within that geometry. This constructed sector, defined by the intersection of the Cornet Cell and the Slit Disk, results in a non-equiregular configuration. Specifically, the resulting sector fails to satisfy the conditions required for equiregularity, as evidenced by the presence of points where the defining functions do not exhibit the necessary smoothness or algebraic properties. This failure is demonstrable through analysis of the sector’s defining equations and the resulting singularity at the intersection.

The construction of non-regular sectors relies on a precise definition of the ‘Section’ within the Cornet Cell in ℝ⁴. These sectors are designed to violate the criteria for closure-finiteness, well-borderedness, and regularity as defined by current conjectures. Specifically, the ‘Section’ is parameterized to induce a non-regular topology, meaning its boundaries do not satisfy the necessary conditions for these properties. This allows for the creation of demonstrably non-regular CAD cells, providing concrete counterexamples that disprove the stated conjectures. The parameters defining the ‘Section’ are crucial; variations result in either regular or non-regular sectors, confirming the sensitivity of these conjectures to cell geometry.

The exploration of Cylindrical Algebraic Decomposition (CAD) reveals a system where seemingly inherent topological properties do not universally hold. This work demonstrates that the contractibility of closures, previously assumed for CAD cells, is not guaranteed, highlighting the nuanced relationship between structure and behavior. As Ernest Rutherford observed, “If you can’t explain it to your grandmother, you don’t understand it well enough.” This principle resonates with the rigorous construction of counterexamples in ℝ⁴; the failure of these conjectures isn’t a flaw, but a call for a deeper understanding of the system’s underlying principles and the limitations of prior assumptions. The paper underscores that optimization in one area-assuming topological well-behavedness-creates tension points elsewhere, demanding a holistic view of the decomposition’s properties.

The Road Ahead

The demonstrated failures of previously held conjectures regarding the topological properties of Cylindrical Algebraic Decomposition (CAD) cells are not merely isolated counterexamples; they represent a fundamental re-evaluation of assumptions surrounding semi-algebraic geometry. The pursuit of closure-finiteness and well-borderedness, once considered inherent characteristics of CAD, now requires a more nuanced understanding of how structure dictates behavior in higher-dimensional spaces. The insistence on regularity, it appears, was an artifact of simplified observation.

Future work must address the implications of these findings for algorithms reliant on CAD. Simplifications predicated on presumed topological properties may introduce instability or, worse, produce incorrect results. A shift in focus toward provably robust, though perhaps less efficient, methods seems warranted. The field should consider whether the pursuit of ‘nice’ decompositions – those exhibiting convenient topological features – is ultimately a misdirection, obscuring the inherent complexity of the underlying spaces.

The question is not simply whether CAD cells are contractible or regular, but whether those properties are necessary for effective computation. Perhaps the beauty of the decomposition lies not in its elegance, but in its ability to capture complexity, even when that complexity resists easy categorization. A living system, after all, thrives on boundaries, not seamless integration.

Original article: https://arxiv.org/pdf/2601.09795.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Decompositional Integrity: The Foundation of Geometric Systems

Sectoral Analysis: Defining Localized Topological Characteristics

Constructing the Counterexample: The Cornet Cell and Sectoral Irregularities

The Road Ahead

See also: