Guiding AI to Verify Code with Structured Reasoning

Author: Denis Avetisyan

A new framework enhances the ability of large language models to formally verify software, improving accuracy and efficiency in critical code analysis.

The BRIDGE experimental architecture facilitates a flexible framework for robotic manipulation, enabling researchers to explore and implement diverse control strategies within a unified system.

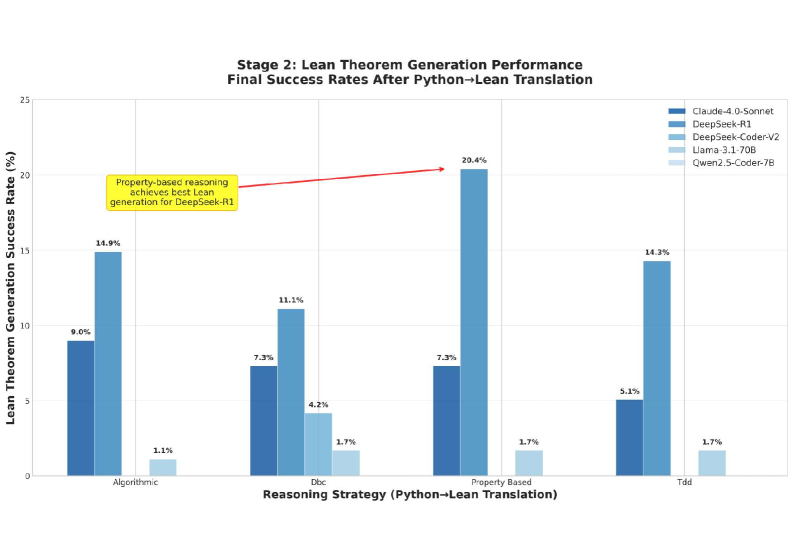
BRIDGE leverages functional programming and domain guidance to significantly advance proof generation and semantic consistency within the Lean4 theorem prover.

Despite recent advances in code generation, large language models still struggle with the rigors of formal program verification. This paper introduces BRIDGE: Building Representations In Domain Guided Program Verification, a framework designed to address this limitation by decomposing verification into interconnected domains of code, specifications, and proofs. BRIDGE elicits distinct reasoning behaviors – functional, specification-driven, and proof-oriented – as intermediate representations to substantially improve both the accuracy and efficiency of verified synthesis, achieving gains in Lean4 and Python environments. Could structured domain alignment and elicited reasoning strategies provide a pathway towards more robust and scalable verified program generation with large language models?

The Algorithm’s Silent Errors: A Verification Challenge

Contemporary software systems are fundamentally built upon intricate algorithms – from the recommendation engines shaping online experiences to the control systems governing critical infrastructure. This reliance, however, presents a substantial verification challenge; as algorithms grow in complexity, the potential for subtle errors increases exponentially. Thorough testing, while a cornerstone of software development, can only demonstrate the absence of errors under specific conditions, leaving a vast space of unexplored inputs and edge cases. The sheer scale of modern codebases, coupled with increasingly sophisticated algorithmic designs, means that guaranteeing correctness through traditional means becomes practically impossible, demanding innovative approaches to ensure reliability and prevent potentially catastrophic failures in systems upon which society increasingly depends.

Despite its prevalence, conventional software testing possesses inherent limitations in achieving complete assurance. While adept at identifying obvious flaws, testing typically explores only a finite subset of potential inputs and scenarios, leaving a vast landscape of possibilities unexamined. This is particularly problematic for complex algorithms where errors can manifest only under specific, rarely encountered conditions. Consequently, even software that passes rigorous testing may harbor subtle bugs that remain dormant until triggered by an unusual user action or unforeseen data combination. The very nature of exhaustive testing – attempting every possible input – is often computationally infeasible, especially as software complexity increases, meaning that a degree of uncertainty always persists, highlighting the need for complementary verification techniques.

While conventional software testing identifies errors through execution with specific inputs, formal verification pursues an alternative: proving a program’s correctness mathematically. This approach aims to establish absolute certainty – guaranteeing a program will always behave as intended, across all conceivable inputs – a level of assurance testing simply cannot provide. However, this rigor historically demanded specialized expertise in logic and theorem proving, presenting a significant barrier to entry for most developers. The process often involved painstakingly crafting formal specifications and then using complex tools to verify that the code adhered to those specifications, a task requiring substantial time and training. Recent advances in automated reasoning and the development of more user-friendly tools are beginning to lower this learning curve, potentially making formal verification a more practical solution for ensuring the reliability of critical software systems.

Specification reasoning consistently improves performance in both Python code generation and Lean4 formal verification compared to baseline approaches.

BRIDGE: Automating Correctness with Language Models

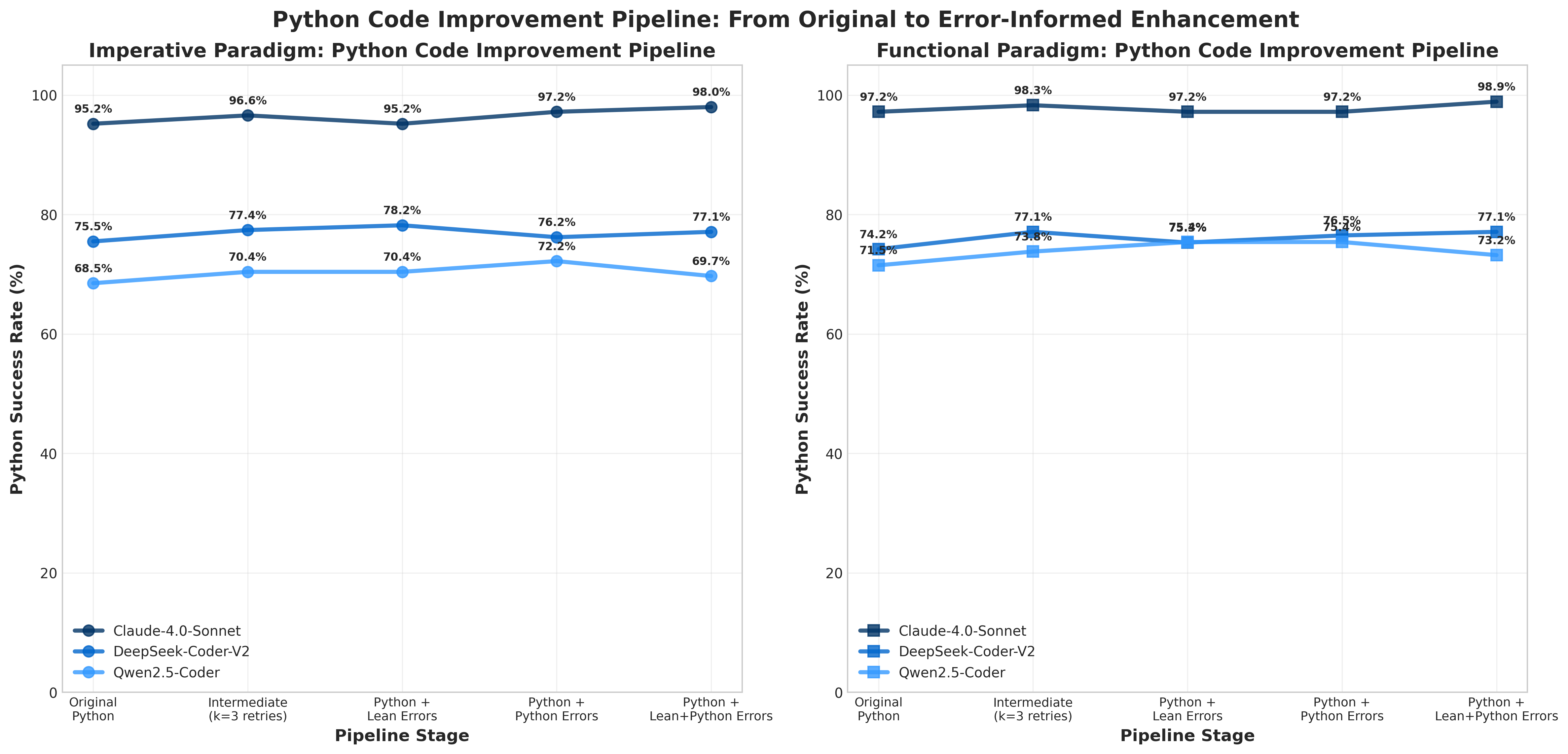
The BRIDGE Framework employs a prompting-based methodology to automate formal verification, thereby lowering the barrier to entry for obtaining correctness guarantees in software. Traditional formal verification requires significant expertise in logic and specialized tools; BRIDGE instead utilizes large language models (LLMs) that are directed, via carefully constructed prompts, to generate formal proofs. This approach shifts the focus from manual proof construction to prompt engineering, allowing users to express desired program behavior and have the LLM attempt to establish its formal validity. The framework’s accessibility stems from its reliance on natural language input and automated proof generation, reducing the need for deep expertise in formal methods.

The BRIDGE Framework utilizes large language models (LLMs) to automate the creation of formal proofs from natural language specifications. This process diminishes the need for extensive manual effort from formal verification experts, as the LLM translates human-readable requirements into a format suitable for automated theorem provers. Specifically, the LLM generates formal logic statements – typically expressed in languages like first-order logic – that represent the desired properties of a system. These generated statements then serve as input to a verification tool, which attempts to prove their correctness. By automating this translation step, BRIDGE lowers the barrier to entry for employing formal verification techniques, making them accessible to a wider range of developers and projects.

The BRIDGE Framework facilitates formal verification through multiple input modalities; it can generate proofs directly from source code, existing unit tests, or high-level natural language descriptions of the desired program behavior. Evaluation of the framework encompassed a dataset of 178 LeetCode problems, assessing performance across five distinct large language models. This broad evaluation scope demonstrates BRIDGE’s adaptability and potential for application with varying LLM architectures and problem domains, moving beyond reliance on a single verification source.

Pass@5 accuracy for Claude 4.0 Sonnet demonstrates that reasoning performance varies with sampling temperature across different prompting strategies-natural language (blue), Python-bridge (green), and OCaml-bridge (orange).

Reasoning Strategies: Functional and Imperative Approaches

BRIDGE utilizes a hybrid reasoning approach, employing both Functional Reasoning and Imperative Reasoning techniques to address the diverse requirements of code verification. The selection between these strategies is determined by the characteristics of the code under analysis; code operating on immutable data structures is effectively verified using Functional Reasoning, while code involving mutable state necessitates Imperative Reasoning. This adaptive methodology allows BRIDGE to handle a wider range of programs than systems limited to a single verification paradigm, increasing overall verification coverage and applicability.

Functional Reasoning in BRIDGE leverages the advantages of Lean4’s dependent type theory and proof assistant when verifying code that utilizes immutable data structures. Lean4’s compositional nature facilitates the breakdown of complex proofs into smaller, more manageable components, increasing verification efficiency. This is because the properties of immutable data – namely, that their state does not change after creation – simplify the reasoning process. Each function application can be considered in isolation, without needing to track state transitions, enabling a more direct and automated approach to proof construction within the Lean4 framework. The system’s ability to express and verify properties of these data structures is central to its effectiveness in this reasoning paradigm.

Verification of code involving mutable state, known as Imperative Reasoning, introduces increased complexity in proof obligations due to the need to track state changes. However, the Lean4 framework provides the necessary tools to effectively address these challenges. Comparative analysis demonstrates that employing Functional Reasoning techniques in conjunction with Lean4 results in a success rate up to 1.5 times greater than baseline imperative verification approaches, indicating a significant improvement in handling mutable state within formal verification workflows.

Functional reasoning paradigms consistently achieve higher pass@5 performance than imperative approaches across various enhancement strategies.

Validation Through Algorithmic Proofs: A Test of Reliability

The application of BRIDGE to the Maximum Beauty Problem serves as a validation case for its capabilities in verifying sorting and searching algorithms. This problem, while seemingly simple, requires rigorous proof of correctness for any proposed solution, especially concerning edge cases and performance characteristics. BRIDGE facilitates this verification by enabling the formalization of algorithm specifications and the subsequent generation of proof obligations. Successful verification demonstrates BRIDGE’s capacity to not only detect algorithmic errors but also to provide a high degree of confidence in the functional correctness of these fundamental algorithms, crucial for a variety of software applications.

The Incremovable Subarray Problem serves as a case study for evaluating the BRIDGE framework’s performance with combinatorial challenges and property-based testing methodologies. This problem involves determining if a given subarray within a larger array can be removed without altering the array’s overall structure, requiring verification of numerous possible subarray configurations. Utilizing BRIDGE, the framework automatically generates and validates properties related to the problem’s constraints and expected behavior. This automated approach contrasts with manual testing, providing a more exhaustive and reliable means of confirming the correctness of solutions designed to address the Incremovable Subarray Problem and similar combinatorial tasks.

Verification of Tree Dynamic Programming (DP) algorithms necessitates rigorous termination proofs to ensure algorithms conclude within a finite number of steps; Lean4 provides the formalization tools and automated tactics to construct and validate these proofs. Implementation of functional reasoning techniques within the Lean4 environment has demonstrably reduced syntax errors in verified Tree DP algorithms from an initial rate of 45% to 12%. This improvement signifies a substantial increase in code correctness and reliability when utilizing formal verification methods for complex algorithmic structures, specifically those involving recursive tree traversals and state management inherent in dynamic programming.

Analysis of proof generation reveals a substantial performance bottleneck transitioning from successful Python code generation (97-98%) to accurate translation into the Lean proof language (9-20%).

Towards Reliable Software: Impact and Future Directions

The development of robust and dependable software is paramount in an increasingly digital world, and the BRIDGE framework directly addresses this need through automated verification. By systematically checking software against its intended specifications, BRIDGE significantly diminishes the potential for errors and security vulnerabilities that can plague critical systems. This automation isn’t merely about speed; it’s about precision, enabling a more thorough examination of code than is often feasible with manual testing. The result is a demonstrable reduction in defects, offering increased confidence in the reliability of software controlling vital infrastructure, medical devices, and other sensitive applications. This proactive approach to error detection ultimately lowers development costs and enhances the safety and security of the digital landscape.

A core strength of the BRIDGE framework lies in its rigorous maintenance of Semantic Consistency throughout the software development lifecycle. This approach doesn’t merely check for syntactical correctness – whether code compiles or a specification is well-formed – but actively verifies that the meaning encoded in each stage – specifications, implemented code, and formal proofs – remains perfectly aligned. By establishing and upholding this semantic link, BRIDGE effectively eliminates a significant source of subtle bugs that often evade traditional testing methods. These bugs arise not from errors in code execution, but from discrepancies between what the software is intended to do, as described in its specifications, and what it actually does, as implemented in code and demonstrated through proofs; the framework’s design actively prevents these mismatches, leading to demonstrably more reliable software systems.

Ongoing development of the BRIDGE framework prioritizes scalability and practical implementation. Researchers aim to broaden its applicability beyond current limitations, enabling verification of increasingly intricate software architectures. A key objective is seamless integration with common development pipelines, minimizing disruption to existing workflows and maximizing adoption. Preliminary results indicate a substantial performance improvement; the framework is projected to achieve pass rates exceeding those of current baseline verification tools by a factor of two, even when generating proofs of comparable length, suggesting a significant leap forward in software reliability and security.

Functional programming consistently yields higher Python code success rates than imperative approaches, and while Lean error feedback improves performance, a substantial gap remains before full verification can be achieved.

The pursuit of formal verification, as demonstrated by BRIDGE, inherently demands a reduction of complexity. The framework’s emphasis on structured reasoning and functional programming isn’t merely about improving accuracy; it’s about distilling problems to their essential components. As Bertrand Russell observed, “To be able to formulate a question is often half the solution.” BRIDGE embodies this principle, transforming the challenge of proof generation into a series of manageable, logically-sound steps. The gains in code synthesis and specification generation aren’t accidental; they are the natural consequence of rigorous clarity-a testament to the power of focused, structural honesty within a complex domain like Lean4.

Where to Next?

The proliferation of tools attempting to mediate between natural language and formal systems inevitably highlights the persistent gulf between them. BRIDGE, by emphasizing structured reasoning within a functional paradigm, offers a momentary reduction in that complexity. Yet, a framework predicated on guiding a large language model tacitly admits its inherent fallibility. The true measure of progress will not be increasingly sophisticated guidance, but the eventual redundancy of it. A system requiring elaborate scaffolding to produce logically sound proofs has, in a sense, already failed to capture the essence of logical thought.

Current work focuses on improving the accuracy of proof generation. A more austere approach would prioritize minimizing the need for generation. Specification generation, too, feels like treating a symptom rather than the disease. If the intent is truly clear, the specification should emerge as a trivial consequence, not a constructed artifact. The pursuit of semantic consistency is valuable, but the ideal remains a system where inconsistency is simply impossible.

The challenge, then, is not to build better intermediaries, but to interrogate the fundamental assumptions underlying the need for translation. To ask not how to make logic more accessible to language, but whether the perceived separation is itself an illusion. Clarity is not merely a feature; it is a courtesy extended to those forced to navigate unnecessarily complex systems.

Original article: https://arxiv.org/pdf/2511.21104.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/