Seeing is Believing: Robots Learn from Watching

by

Author: Denis Avetisyan

New research demonstrates a method for soft robots to learn complex movements simply by observing video, unlocking more intuitive and adaptable control.

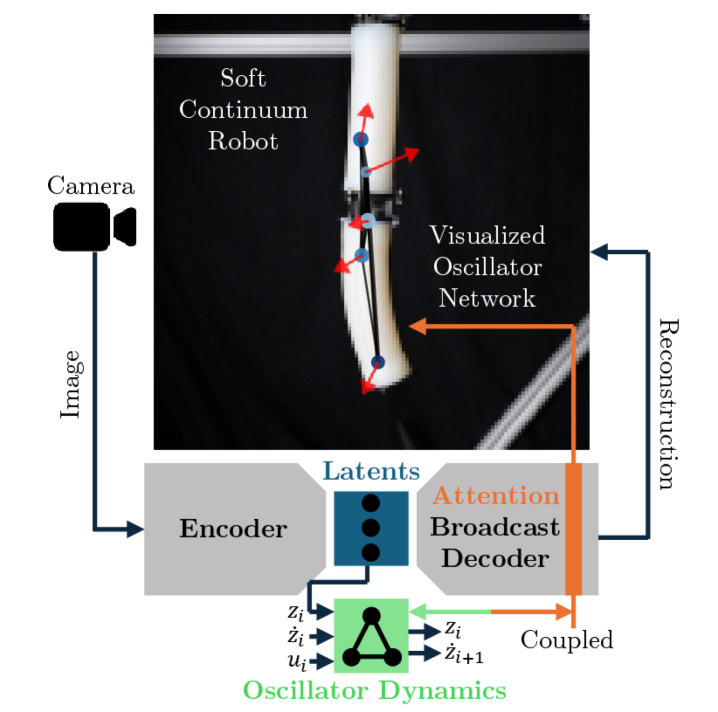
This study introduces an attention broadcast decoder (ABCD) - a plug-and-play component for learning the dynamics of soft continuum robots via autoencoders and Koopman operator theory-and uniquely couples the decoder’s attention maps to two-dimensional oscillator dynamics, enabling visualization of network-learned parameters like masses, stiffnesses, and actuation forces directly onto reconstructed or predicted images.
This study introduces an attention broadcast decoder (ABCD) – a plug-and-play component for learning the dynamics of soft continuum robots via autoencoders and Koopman operator theory-and uniquely couples the decoder’s attention maps to two-dimensional oscillator dynamics, enabling visualization of network-learned parameters like masses, stiffnesses, and actuation forces directly onto reconstructed or predicted images.

An attention-based decoder integrated with Koopman operators and oscillator networks enables interpretable learning of soft robot dynamics directly from visual data.

Learning the dynamics of soft continuum robots from visual data remains challenging, often sacrificing physical interpretability for data-driven flexibility or requiring costly prior knowledge. This work, ‘Learning Visually Interpretable Oscillator Networks for Soft Continuum Robots from Video’, addresses this gap by introducing an attention-based decoder-the ABCD-that, when paired with oscillator networks, reveals interpretable and accurate representations of robot behavior directly from video. The resulting models not only improve multi-step prediction accuracy-demonstrating up to 5.7x error reduction-but also autonomously discover physically meaningful structures like chains of oscillators. Could this fully data-driven approach unlock more intuitive and robust control strategies for soft robots operating in complex environments?

The Echo of Hidden Forces

Many systems encountered in nature and society – from weather patterns and financial markets to biological networks and social interactions – are governed by forces that are not immediately obvious. These systems possess hidden dynamics – underlying principles and relationships that shape their behavior but remain obscured within the complexity of observed data. Effectively modeling these systems necessitates going beyond surface-level observations and uncovering these latent drivers. A complete understanding requires identifying the root causes of change, the feedback loops that amplify or dampen effects, and the interdependencies between various components. Without acknowledging and accounting for these hidden processes, models risk providing inaccurate predictions and failing to capture the true essence of the system’s behavior, leading to flawed decision-making and limited predictive power.

Many conventional system modeling techniques falter when confronted with the inherent complexities of real-world phenomena. Direct analysis of raw data streams often proves insufficient, as these streams contain noise, irrelevant information, and fail to explicitly reveal the underlying causal relationships driving system behavior. Consequently, predictions generated from these approaches can be significantly inaccurate, particularly when extrapolating beyond the observed data. This limitation arises because traditional methods treat each data point as independent, overlooking the temporal dependencies and feedback loops crucial to understanding dynamic systems. The inability to discern these hidden patterns results in models that are brittle, lack generalizability, and ultimately fail to capture the nuanced intricacies of the system they aim to represent, hindering effective forecasting and control.

The pursuit of accurate system modeling increasingly relies on the ability to distill complex behaviors into readily understandable forms. Rather than grappling with the full dimensionality of raw data – which often obscures crucial relationships – researchers are focusing on discovering latent representations. These representations involve mapping high-dimensional system states onto a lower-dimensional space, effectively capturing the essential dynamics while discarding noise or irrelevant details. This dimensionality reduction isn’t merely about simplification; it aims to reveal underlying patterns and control parameters that govern the system’s evolution. By expressing dynamics in this compressed, interpretable space, models become more robust, generalizable, and capable of predicting future states with greater accuracy, ultimately offering a more insightful understanding of the system’s inherent mechanisms. Such approaches are proving vital in fields ranging from climate modeling to biological systems analysis, where uncovering hidden variables is paramount.

The 2D oscillator networks accurately model the simulated robot's dynamics, predicting future states 20 steps ahead and visualizing key parameters like mass, stiffness, and actuation forces to enhance clarity.
The 2D oscillator networks accurately model the simulated robot’s dynamics, predicting future states 20 steps ahead and visualizing key parameters like mass, stiffness, and actuation forces to enhance clarity.

Unveiling the System’s Blueprint: Representation Learning

Representation learning is a subset of machine learning concerned with discovering and utilizing effective data representations without explicit human engineering. Traditional machine learning algorithms often require hand-crafted features, a process which is both time-consuming and potentially suboptimal. Representation learning aims to automate this process, enabling algorithms to learn features directly from raw data. These learned representations, often in the form of lower-dimensional embeddings, are designed to capture the salient characteristics of the input data, facilitating improved performance on downstream tasks such as classification, prediction, and anomaly detection. The core principle is to transform data into a format that makes it easier for algorithms to extract meaningful patterns and generalize to unseen examples.

Autoencoders are neural networks trained to copy their input to their output. This is achieved through a bottleneck layer, forcing the network to learn a compressed, efficient representation of the input data. The network consists of an encoder, which maps the input to this lower-dimensional latent space, and a decoder, which reconstructs the original input from the latent representation. Training minimizes a reconstruction loss, typically mean squared error, between the input and the decoded output. This architecture compels the network to learn salient features necessary for accurate reconstruction, effectively learning a data representation without explicit labeling.

Autoencoders achieve dimensionality reduction by encoding input data into a lower-dimensional latent space, and then decoding it back to its original form. This process forces the network to learn a compressed, efficient representation of the data, capturing only the most salient features necessary for accurate reconstruction. The resulting latent space, typically of significantly reduced dimensionality compared to the input, effectively distills the essential dynamics of the data, discarding noise and redundant information. Reconstruction loss, calculated as the difference between the input and the reconstructed output, serves as the primary training signal, guiding the autoencoder to learn representations that minimize information loss during compression and decompression. The dimensionality of the latent space is a hyperparameter, controlling the degree of compression and the level of detail retained in the learned representation.

The attention broadcast decoder integrates with an autoencoder to learn image reconstruction by retrieving and spatially broadcasting attention maps and attended latents via an attention processor.
The attention broadcast decoder integrates with an autoencoder to learn image reconstruction by retrieving and spatially broadcasting attention maps and attended latents via an attention processor.

Forecasting the Inevitable: Dynamics Within the Latent Realm

The capacity for multi-step prediction in complex systems is significantly enhanced by representing system dynamics within a lower-dimensional latent space. This approach allows for the identification and modeling of underlying patterns and relationships that would be obscured in the original, high-dimensional state space. By embedding the dynamics in this latent space, prediction algorithms can more efficiently extrapolate future states based on observed trajectories. This is particularly useful for systems exhibiting non-linear behavior where traditional forecasting methods may fail. The reduced dimensionality also minimizes computational cost and improves the robustness of the predictive model, enabling accurate forecasts over extended time horizons.

Koopman Operator Theory and Oscillator Networks provide methods for modeling the underlying dynamics of complex systems within a latent space. Koopman Operator Theory linearizes nonlinear dynamical systems via an infinite-dimensional operator, allowing for prediction using linear methods. Oscillator Networks, conversely, represent system states as combinations of harmonic oscillators, effectively capturing cyclical or oscillatory behaviors. Both techniques transform the problem of predicting system evolution into a more tractable form suitable for extrapolation; Koopman theory maps observations to a higher-dimensional space where dynamics are linear, while oscillator networks decompose dynamics into frequency components. These approaches enable the prediction of future states based on observed data by learning and applying the respective operator or network representation of the system’s behavior.

Implementation of the Attention Broadcast Decoder (ABCD) in conjunction with Koopman Operators resulted in a 5.7-fold reduction in multi-step prediction error when applied to a 2-segment soft robot. Specifically, the combined approach achieved a Mean Squared Error (MSE) of $9.84e-4$. This represents a significant improvement over a standard Koopman operator-based prediction method, which yielded an MSE of $5.66e-3$ under the same conditions. The data indicates that the ABCD effectively enhances the predictive capability of the Koopman framework in this robotic system.

Performance improvements were observed when the Attention Broadcast Decoder (ABCD) was integrated with 2D oscillator networks. Specifically, the combined approach yielded a Mean Squared Error (MSE) of $6.56e-3$. This represents a significant reduction in error compared to the standard 2D oscillator network implementation, which achieved an MSE of $2.27e-2$. The data indicates that the ABCD enhances the predictive capabilities of oscillator networks, resulting in more accurate dynamic modeling.

Attention-based models (ABCD) effectively predict smooth bending transitions in 2-segment robots by extrapolating between latent states, unlike standard models which yield erratic, non-bent configurations.
Attention-based models (ABCD) effectively predict smooth bending transitions in 2-segment robots by extrapolating between latent states, unlike standard models which yield erratic, non-bent configurations.

Beyond the Known: Generalization and the Promise of Extrapolation

The true power of latent space extrapolation lies not merely in replicating observed behaviors, but in venturing beyond their confines. A well-constructed latent space doesn’t simply remember the past; it understands the underlying principles governing the data, allowing it to intelligently interpolate and extrapolate – to envision plausible outcomes for entirely new scenarios. This is achieved by compressing complex data into a lower-dimensional code – the latent vector – where smooth transitions between known data points suggest probable outcomes for unseen combinations. Essentially, the system learns the rules, not just the examples, and can therefore generate reasonable predictions even when confronted with conditions it has never explicitly experienced. This capacity is crucial in dynamic systems, offering a pathway to proactive decision-making and robust performance in uncertain environments.

The translation of these abstract predictions into recognizable forms relies heavily on the process of image reconstruction, a process intrinsically linked to the architecture of the autoencoder. This neural network learns a compressed, efficient representation of input data – the latent space – and crucially, also learns to decode this representation back into its original form. Following a prediction within the latent space – perhaps envisioning a future state or a novel configuration – the autoencoder effectively reverses its compression, generating an observable output corresponding to that predicted point. This reconstruction isn’t simply a mirroring of training data; it’s a synthesis, allowing the system to visualize and present predictions for scenarios never explicitly encountered, and offering a bridge between the mathematical realm of latent variables and the visual world of interpretable images.

The ability to accurately predict system behavior in unfamiliar scenarios represents a significant advancement across numerous fields. Applications demanding reliable performance beyond the confines of training data – such as autonomous navigation in unpredictable weather, medical diagnosis with rare conditions, or financial forecasting during market disruptions – greatly benefit from this extrapolation capability. By effectively generalizing learned patterns, these systems aren’t simply recalling memorized data, but are instead constructing plausible outcomes for previously unseen inputs. This is particularly vital in dynamic environments where complete datasets are impossible to obtain, or where unexpected events regularly occur; robust predictions enable proactive responses and mitigate potential risks, transforming systems from reactive tools into adaptable and resilient agents.

Single-segment robots consistently achieve accurate multi-step reconstructions, while the ABCD method improves long-term reconstruction accuracy for two-segment robots using both Koopman and oscillator network dynamics.
Single-segment robots consistently achieve accurate multi-step reconstructions, while the ABCD method improves long-term reconstruction accuracy for two-segment robots using both Koopman and oscillator network dynamics.

The pursuit of dynamics modeling, as demonstrated in this work with oscillator networks and attention-based decoders, reveals a fundamental truth: every system, even one as fluid as a soft robot, ultimately succumbs to the passage of time. The ABCD architecture attempts not merely prediction, but a graceful acceptance of inherent system limitations, extracting meaningful latent dynamics from video data. As John McCarthy observed, “It is better to solve one problem completely than to solve many problems partially.” This research embodies that principle, focusing on interpretable representations rather than brute-force complexity, acknowledging that a deeper understanding of a few core principles-like those captured by Koopman operators-outweighs superficial accuracy across a broader, less understood scope. Each failure in prediction, then, isn’t an error, but a signal from time, guiding refinement towards a more resilient and insightful model.

What’s Next?

The pursuit of interpretable dynamics, as demonstrated by this work, inevitably encounters the limits of representation. The attention-based decoder offers a compelling step towards distilling physically meaningful states from raw sensory input, but this is merely a localized equilibrium. The true challenge lies not in finding these states, but in acknowledging their transient nature. Uptime, in any complex system, is a rare phase of temporal harmony, inevitably yielding to decay and reconfiguration.

Future iterations must address the brittleness inherent in learned models. The current approach, while effective, remains tethered to the specific conditions of the training data. The next generation of oscillator networks will need to incorporate mechanisms for self-diagnosis and adaptation, effectively building systems that anticipate and accommodate their own degradation. Technical debt, in this context, is akin to erosion – a constant force that demands ongoing maintenance and strategic reinforcement.

Ultimately, the field edges closer to a synthesis of learning and control. However, the enduring question isn’t whether a robot can learn to move, but whether it can learn to accept its eventual immobility. The pursuit of perfect prediction is a fallacy; the art lies in designing systems that age gracefully, relinquishing control with dignity as entropy asserts its dominion.

Original article: https://arxiv.org/pdf/2511.18322.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-26 00:55