Designing with Confidence: AI Meets Physics for Robust Metasurfaces

by

Author: Denis Avetisyan

A new optimization framework leverages physics-based uncertainty to dramatically improve the reliability and efficiency of AI-driven metasurface design.

A robust design optimization workflow leverages uncertainty quantification-specifically, physics-based rules-to efficiently balance exploration and exploitation, mitigating the risk of erroneous designs that can arise when single-fidelity surrogates deviate from the training distribution during metasurface design.
A robust design optimization workflow leverages uncertainty quantification-specifically, physics-based rules-to efficiently balance exploration and exploitation, mitigating the risk of erroneous designs that can arise when single-fidelity surrogates deviate from the training distribution during metasurface design.

This work introduces a method for quantifying uncertainty in AI-driven inverse design, reducing the need for computationally intensive simulations and enabling more robust performance.

Efficiently designing complex physical systems often requires navigating a trade-off between computational cost and solution reliability. The work ‘Physics-Informed Uncertainty Enables Reliable AI-driven Design’ introduces a novel optimization framework that addresses this challenge for inverse design problems, specifically in the context of frequency-selective surfaces. By leveraging violations of fundamental physical laws as a proxy for predictive uncertainty, this approach dramatically increases design success rates-from under 10% to over 50%-while simultaneously reducing computational demands by an order of magnitude. Could this physics-informed approach unlock a new era of robust and autonomous scientific discovery across a wider range of engineering disciplines?

Navigating Complexity in Frequency-Selective Surface Design

The creation of Frequency-Selective Surfaces (FSS) for cutting-edge technologies – encompassing applications like 5G communications, radar systems, and advanced sensors – presents a significant design challenge due to the sheer complexity of the parameter space involved. These surfaces, often constructed from meticulously patterned metallic layers, achieve their functionality through the interaction of electromagnetic waves with these structures; even minor variations in the size, shape, or arrangement of the constituent elements dramatically alter the FSS’s performance. Consequently, designers must explore a vast multidimensional landscape of possible configurations – encompassing parameters like unit cell geometry, substrate material, and layer thickness – to identify optimal designs that meet stringent performance criteria. This exploration is further complicated by the need to simultaneously optimize multiple, often conflicting, objectives, such as bandwidth, polarization sensitivity, and angular stability, making the design process computationally intensive and demanding.

The design of advanced electromagnetic devices, such as Frequency-Selective Surfaces, often necessitates exploring a vast parameter space to achieve optimal performance. However, relying exclusively on computationally intensive, high-fidelity simulations for each design iteration quickly becomes impractical. These simulations, while accurate, demand significant processing time and resources, effectively restricting the number of designs that can be thoroughly investigated. This limitation hinders the potential for discovering truly innovative solutions and can lead to suboptimal designs that merely satisfy baseline requirements. Consequently, researchers are increasingly focused on developing surrogate models and efficient optimization algorithms to navigate these complex design landscapes more effectively, enabling broader exploration and accelerating the development of next-generation technologies.

Robust design of frequency-selective surfaces demands a thorough understanding of potential uncertainties, as even slight variations in manufacturing or operational conditions can significantly degrade performance. However, accurately quantifying these uncertainties presents a substantial challenge; traditional methods like Monte Carlo simulations, while conceptually straightforward, require an impractically large number of computationally expensive high-fidelity electromagnetic simulations. Furthermore, simpler, less costly approaches often rely on assumptions about uncertainty distributions that may not hold true for complex FSS geometries or material properties, leading to imprecise or overly optimistic estimations of design robustness. Consequently, researchers are actively exploring surrogate modeling techniques and advanced statistical methods to achieve a balance between computational efficiency and the fidelity needed for reliable uncertainty quantification, ultimately enabling the creation of FSS designs that consistently meet performance goals despite real-world variability.

Periodic arrangements of meta-atoms, as illustrated by the [latex]18 imes 18[/latex] and [latex]36 imes 36[/latex] pixel designs, are commonly used to create frequency-selective surfaces and other functional devices.
Periodic arrangements of meta-atoms, as illustrated by the [latex]18 imes 18[/latex] and [latex]36 imes 36[/latex] pixel designs, are commonly used to create frequency-selective surfaces and other functional devices.

Balancing Fidelity: A Multi-Level Optimization Strategy

Multi-Fidelity Optimization (MFO) enhances design space exploration by strategically combining computationally inexpensive, low-fidelity models – such as simplified physics or reduced-order models – with high-fidelity simulations that offer greater accuracy but require significant computational resources. This approach avoids the limitations of solely relying on either method; exhaustive searches with low-fidelity models can be performed initially, followed by targeted refinement using high-fidelity evaluations only on the most promising designs. The efficiency gains stem from minimizing the number of costly high-fidelity simulations required to achieve an optimal solution, effectively balancing computational cost with solution accuracy.

The Constant Attraction Phase of multi-fidelity optimization utilizes low-fidelity models – computationally inexpensive approximations of the true simulation – to perform an initial, broad exploration of the design space. This phase prioritizes quantity of evaluations over precision, aiming to quickly identify regions exhibiting favorable objective function values. By leveraging these surrogate models, a large number of design candidates can be assessed with minimal computational cost, effectively narrowing the search area before committing to more expensive, high-fidelity simulations. The resulting data informs the subsequent refinement stages by focusing computational resources on the most promising areas identified during this initial sweep.

The Alternating Strategy Phase of multi-fidelity optimization utilizes high-fidelity evaluations to refine designs identified during the initial low-fidelity exploration. This phase iteratively assesses candidate solutions with the computationally expensive, but accurate, high-fidelity model. The process alternates between exploiting promising regions – performing focused evaluations around existing best solutions – and exploring the design space to prevent premature convergence on local optima. This balanced approach ensures that designs are not only optimized based on accurate simulations, but also that the search process effectively navigates the complexity of the design space, improving the likelihood of finding a globally optimal solution. The frequency of high-fidelity evaluations is strategically managed to balance accuracy with computational cost.

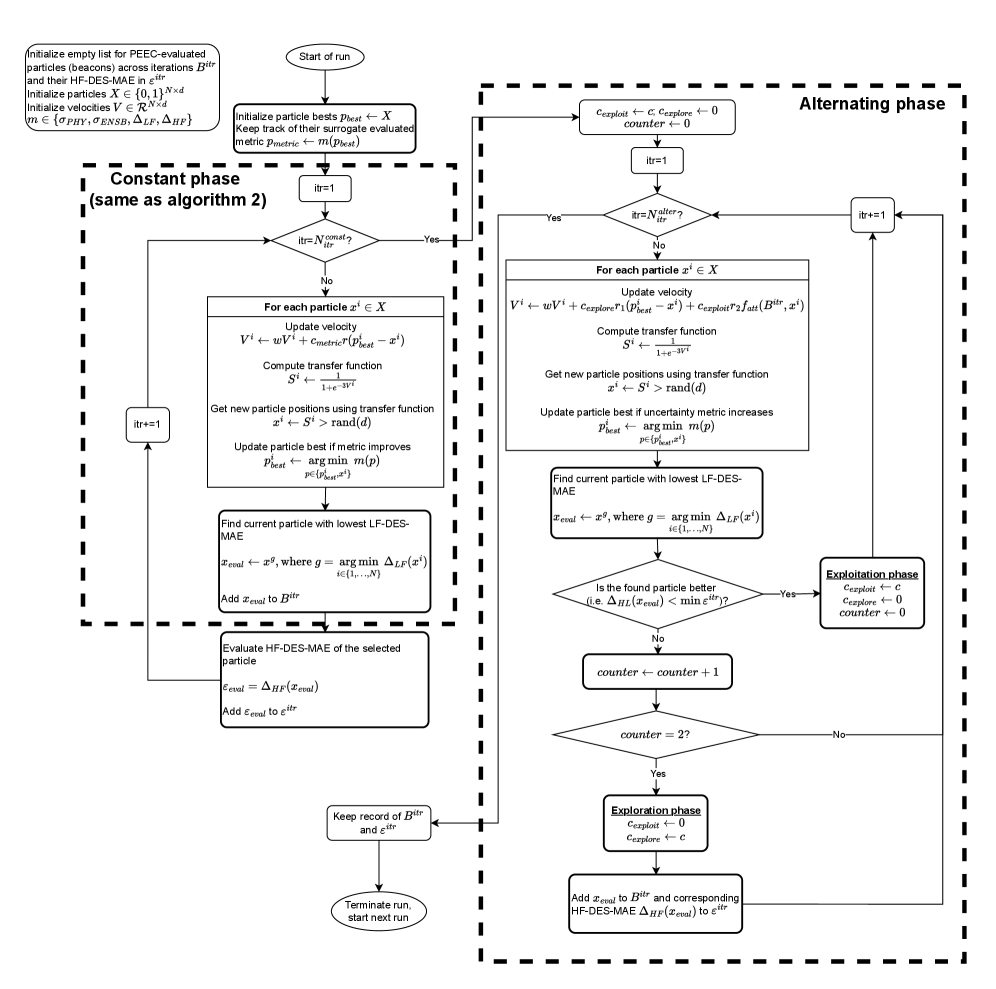
The two-stage multi-fidelity optimization algorithm alternates between a constant-fidelity phase and an alternating-fidelity phase to efficiently search the design space.
The two-stage multi-fidelity optimization algorithm alternates between a constant-fidelity phase and an alternating-fidelity phase to efficiently search the design space.

Harnessing Particle Swarms and Physics-Informed Reliability

Particle Swarm Optimization (PSO) is utilized as the core optimization algorithm due to its efficiency in traversing complex design spaces defined by varying fidelity levels. This multi-fidelity approach involves evaluating designs with different computational costs – lower fidelity models offer rapid assessment but reduced accuracy, while higher fidelity models are computationally expensive but provide precise results. PSO leverages a population of particles, each representing a potential design, and iteratively adjusts their positions based on their own best-known position and the swarm’s overall best position. This process effectively balances exploration of the design space with exploitation of promising regions, enabling efficient identification of optimal designs even with the computational constraints imposed by high-fidelity simulations. The algorithm’s inherent parallelism further accelerates the optimization process, particularly when coupled with distributed computing resources.

Physics-Informed Uncertainty estimation quantifies prediction reliability by evaluating the consistency of simulation results with established physical laws, specifically Maxwell’s Equations. This process involves analyzing the solution’s adherence to these equations; deviations indicate potential inaccuracies or instabilities in the prediction. Unlike traditional uncertainty quantification methods which rely solely on statistical sampling, this approach leverages the underlying physics to provide a more principled and efficient assessment of error. The magnitude of deviation from [latex]∇ ⋅ \mathbf{D} = \rho[/latex] and other Maxwell’s equations directly informs the uncertainty estimate, enabling robust design optimization by flagging potentially invalid or unrealistic solutions before further computation.

Traditional optimization of electromagnetic structures often relies on computationally expensive simulations or simplified models that may lack accuracy, leading to designs with unpredictable performance. This approach, integrating Physics-Informed Uncertainty, provides a more trustworthy evaluation by quantifying prediction reliability based on adherence to Maxwell’s Equations. This quantification allows the optimization algorithm to prioritize designs where the solution space is well-constrained by physical laws, effectively discounting solutions exhibiting high uncertainty due to potential violations of fundamental physics. For complex geometries and material compositions where standard methods struggle to converge or produce consistent results, this physics-informed assessment significantly improves the robustness and dependability of the optimized design.

Design optimization using a baseline BPSO algorithm, evaluated by [latex]LF-DES-MAE[/latex] for convergence and [latex]HF-DES-MAE[/latex] for performance, successfully generated both band-stop and band-pass profiles as demonstrated by the convergence curves and cumulative frequency distributions of the lowest error metrics across 100 optimization runs.
Design optimization using a baseline BPSO algorithm, evaluated by [latex]LF-DES-MAE[/latex] for convergence and [latex]HF-DES-MAE[/latex] for performance, successfully generated both band-stop and band-pass profiles as demonstrated by the convergence curves and cumulative frequency distributions of the lowest error metrics across 100 optimization runs.

Validating Accuracy and Demonstrating System Performance

To rigorously assess the accuracy of predictions generated by both low- and high-fidelity models, the research employs the metrics ‘LF-DES-MAE’ and ‘HF-DES-MAE’. These metrics, standing for Low-Fidelity Discrepancy Error – Mean Absolute Error and High-Fidelity Discrepancy Error – Mean Absolute Error respectively, quantify the average absolute difference between the model’s predictions and the true, high-fidelity results. By focusing on minimizing these error values, the study ensures that the computationally efficient, low-fidelity surrogate models effectively capture the essential behavior of the Frequency-Selective Surface, allowing for optimization without sacrificing predictive power. Essentially, these metrics serve as a critical yardstick for validating the fidelity of the approximations and the overall reliability of the multi-fidelity optimization framework.

The efficacy of surrogate models in accelerating Frequency-Selective Surface (FSS) design hinges on their ability to accurately mimic the behavior of computationally expensive, high-fidelity simulations. Minimizing the errors quantified by metrics like LF-DES-MAE and HF-DES-MAE is therefore paramount; these errors directly reflect the discrepancy between the surrogate’s predictions and the true FSS response. A low-error surrogate doesn’t simply approximate the behavior, but effectively represents it, allowing optimization algorithms to explore the design space with confidence. This ensures that improvements identified using the fast, low-fidelity model will translate reliably to performance gains when validated with the full, high-fidelity simulation, ultimately streamlining the design process and achieving optimal FSS performance.

The optimization process benefitted significantly from a multi-fidelity approach, yielding results on par with traditional, computationally expensive high-fidelity optimization methods. Specifically, the framework achieved a comparable reduction in the high-fidelity Discrete Element Smoothness – Mean Absolute Error [latex]HF-DES-MAE[/latex] while dramatically decreasing the required processing time. This represents an approximate ten-fold reduction in runtime, enabling more efficient exploration of the design space and faster convergence towards optimal Frequency-Selective Surface configurations. The ability to maintain accuracy with significantly reduced computational cost positions this multi-fidelity framework as a powerful tool for complex engineering optimization problems.

Evaluations demonstrate a notable performance difference between optimization targets; the multi-fidelity framework consistently achieved a 100% success rate in optimizing for band-pass frequency-selective surface profiles. However, optimization for band-stop profiles yielded a success rate of approximately 50%. This disparity suggests that the characteristics of band-stop designs present a greater challenge for the surrogate models and optimization algorithms employed, potentially requiring more extensive exploration of the design space or more accurate low-fidelity representations to achieve consistently high performance across all target profiles. Further investigation into the specific factors contributing to this difference is warranted to refine the multi-fidelity optimization process and enhance its robustness for diverse frequency-selective surface designs.

A surrogate model trained with increased data accurately predicts the real and imaginary components of transmission and reflection (∼20-30 GHz) as validated by comparison with a high-fidelity numerical solver.
A surrogate model trained with increased data accurately predicts the real and imaginary components of transmission and reflection (∼20-30 GHz) as validated by comparison with a high-fidelity numerical solver.

The pursuit of efficient metasurface design, as detailed in this work, necessitates a holistic understanding of the interplay between optimization algorithms and underlying physical principles. This approach echoes the sentiment of Henri Poincaré, who stated, “It is through science that we arrive at truth, but it is through art that we express it.” The framework presented doesn’t merely seek a solution; it actively quantifies the inherent uncertainties within the physics itself, allowing for designs that are not only performant but also robust. Just as one cannot replace the heart without understanding the bloodstream, this method recognizes that a localized change in design parameters inevitably impacts the entire system, demanding consideration of the broader physical context. The integration of physics-informed machine learning and uncertainty quantification creates a synergistic effect, enhancing the reliability of AI-driven design processes.

Beyond the Simulation

The pursuit of automated design, particularly for complex structures like metasurfaces, invariably encounters a fundamental trade-off. This work rightly identifies that minimizing computational cost often necessitates sacrificing fidelity – but the presented framework offers a path towards intelligently managing that loss. The true limitation, however, lies not within the optimization algorithm itself, but in the very act of defining ‘good’ design. Current metrics tend toward single-objective optimization, neglecting the inevitable cascade of secondary effects that arise when a structure interacts with a real, imperfect world. A truly robust design process must account for manufacturing tolerances, environmental variations, and the long-term degradation of materials – factors currently treated as externalities.

The integration of uncertainty quantification is a necessary step, yet it also exposes a deeper problem. Each added layer of probabilistic modeling introduces further assumptions, and these assumptions, not the physics, become the dominant source of error. The system’s complexity increases, and its behavior becomes increasingly opaque. The architecture, previously invisible when functioning, becomes glaringly apparent upon failure. Future efforts should focus not on more sophisticated models, but on simplifying the problem itself – on identifying the essential parameters and accepting a degree of inherent imperfection.

Ultimately, the cost of freedom isn’t merely computational; it’s conceptual. The ability to explore a vast design space comes with the burden of defining what constitutes a meaningful solution. This work offers a valuable tool, but it is the clarity of purpose, not the elegance of the algorithm, that will determine its ultimate impact.

Original article: https://arxiv.org/pdf/2601.18638.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-01-28 00:39