Beyond Equivariance: A New Path for Accurate Molecular Simulations

by

Author: Denis Avetisyan

Researchers are challenging conventional wisdom in machine learning for materials science with a surprisingly effective approach to interatomic potential development.

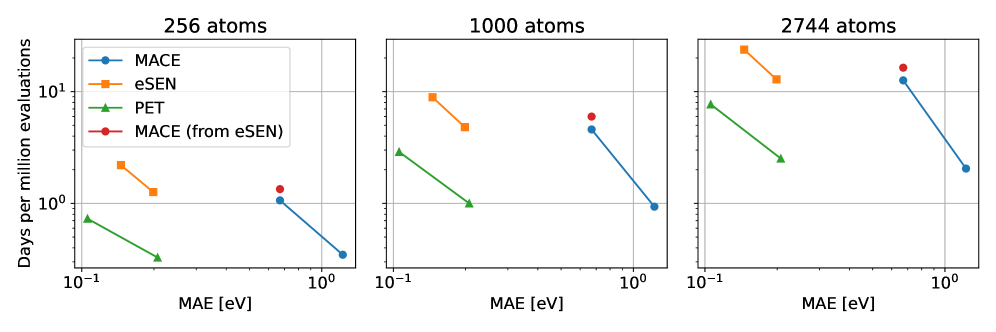
The study demonstrates an accuracy-speed Pareto front achieved by models trained on the SPICE dataset at varying atomic scales, with computational timings for MACE evaluations aligning closely with previously reported results and likely influenced by hardware configurations.
The study demonstrates an accuracy-speed Pareto front achieved by models trained on the SPICE dataset at varying atomic scales, with computational timings for MACE evaluations aligning closely with previously reported results and likely influenced by hardware configurations.

Rotationally unconstrained graph neural networks demonstrate comparable accuracy and speed to state-of-the-art equivariant models for large-scale atomistic simulations.

Replacing computationally expensive electronic-structure calculations with machine-learned interatomic potentials (MLIPs) offers a path to simulating materials at scale, yet commonly employed models enforce strict physical constraints. This work, ‘Pushing the limits of unconstrained machine-learned interatomic potentials’, investigates whether relaxing these constraints-particularly rotational equivariance-can surprisingly improve both the efficiency and accuracy of MLIPs when trained with large datasets. We demonstrate that unconstrained graph neural networks can achieve comparable or superior performance to their constrained counterparts in benchmark accuracy and practical simulations, such as geometry optimization and lattice dynamics. Could this approach unlock even more scalable and accurate atomistic simulations by circumventing the complexities of enforcing strict physical symmetries?

The Atomic Landscape: Mapping Energy Through Interatomic Potentials

Computational materials science fundamentally depends on the ability to map the energy of a material as its atoms rearrange – an ā€˜energy landscapeā€™ – and this is achieved through interatomic potentials. These potentials act as mathematical functions that approximate the complex quantum mechanical interactions between atoms, allowing researchers to predict a materialā€™s behavior without solving the computationally expensive Schrƶdinger equation directly. The accuracy of these potentials is paramount; even slight inaccuracies can lead to drastically incorrect predictions of material properties, like strength, conductivity, or thermal expansion. Consequently, significant effort is devoted to developing and refining these potentials, ranging from simple pairwise interactions to sophisticated many-body formulations, all striving to balance accuracy with computational efficiency and enabling the simulation of materials ranging from everyday plastics to the exotic compounds found in extreme environments.

The efficiency of computational materials science hinges on the principle of locality, which posits that atomic interactions diminish rapidly with distance. This short-ranged nature significantly simplifies the construction of interatomic potentials, as only neighboring atoms need to be explicitly considered in calculations. However, this simplification demands a careful formulation of the potential; while long-range forces can often be neglected, the functional form describing even short-range interactions must be accurate to capture the subtle nuances of chemical bonding and material properties. Failing to do so can introduce errors that accumulate and compromise the reliability of simulations, necessitating a balance between computational efficiency and the fidelity of the atomic description. Consequently, researchers devote considerable effort to developing potential functions that accurately represent the local energy landscape, ensuring that materials are modeled with sufficient precision.

The reliability of computational models in materials science hinges on the careful consideration of fundamental symmetries within interatomic potentials. Specifically, permutational invariance-the principle that swapping the order of atoms in a system shouldn’t alter the overall energy-is paramount. Without this symmetry, a model might predict different energies for identical configurations simply due to atom labeling, leading to physically unrealistic results and invalidating simulations. Constructing potentials that adhere to this invariance typically involves formulating the energy as a sum of contributions dependent on atom pairs, triples, or higher-order groupings, rather than individual atom indices. This ensures that the potential energy remains consistent regardless of how atoms are numbered, providing a robust and physically meaningful description of atomic interactions and enabling accurate predictions of material properties.

The proposed architecture calculates total energy by summing atomic energies [latex]E_i[/latex] for each atom and its neighbors, utilizing attention weights scaled for smoothness as detailed in Ref. [9].
The proposed architecture calculates total energy by summing atomic energies [latex]E_i[/latex] for each atom and its neighbors, utilizing attention weights scaled for smoothness as detailed in Ref. [9].

Simulating the Dance of Atoms: Core Computational Methods

Molecular Dynamics (MD) simulations model the time-dependent behavior of atoms and molecules by numerically solving Newtonā€™s equations of motion, [latex]F = ma[/latex], for each atom in the system. These calculations require a defined interatomic potential, also known as a force field, which mathematically describes the potential energy of the system as a function of atomic positions. The force on each atom is derived from the gradient of this potential energy surface. MD integrates these equations over time, typically using the Verlet algorithm or similar methods, to generate trajectories of atomic positions, velocities, and accelerations. This allows for the observation of dynamic processes, such as diffusion, phase transitions, and chemical reactions, at the atomic scale. The accuracy of an MD simulation is heavily dependent on the quality of the interatomic potential used and the chosen simulation parameters, including timestep and ensemble.

Geometry optimization is a computational method used to determine the lowest energy arrangement of atoms within a material structure. This process relies on interatomic potentials – mathematical functions describing the energy interaction between atoms – to calculate the forces acting on each atom. An iterative algorithm then adjusts the atomic positions, minimizing the overall potential energy of the system until a stable equilibrium is reached. The resulting configuration represents the structure’s minimum energy conformation and is considered a stable state, essential for predicting material properties and behavior. The accuracy of the optimization is dependent on both the chosen interatomic potential and the convergence criteria used to define the minimum energy state.

Monte Carlo simulation utilizes random sampling to investigate the potential energy landscape of a system, determined by defined interatomic potentials. This method generates a series of configurations by randomly perturbing the atomic positions, accepting or rejecting these moves based on the Metropolis algorithm to ensure configurations are sampled according to a Boltzmann distribution. By statistically analyzing the accepted configurations, properties such as free energy, enthalpy, entropy, and heat capacity can be calculated as an ensemble average. The efficiency of Monte Carlo simulations depends on the choice of move sets and the accuracy of the interatomic potential used to evaluate the energy of each proposed configuration. Unlike Molecular Dynamics, Monte Carlo does not rely on time propagation, making it suitable for exploring static thermodynamic properties and systems with high energy barriers.

Using the PET-OAM method, geometry optimization and subsequent phonon calculations reveal that both BCC and HCP titanium configurations converge to stable structures with distinct vibrational properties, as demonstrated by their phonon bands and vibrational densities of states.
Using the PET-OAM method, geometry optimization and subsequent phonon calculations reveal that both BCC and HCP titanium configurations converge to stable structures with distinct vibrational properties, as demonstrated by their phonon bands and vibrational densities of states.

Beyond the Derivative: A New Paradigm for Force Prediction

The calculation of interatomic forces using conventional methods necessitates the differentiation of interatomic potential energy functions with respect to atomic positions. This differentiation process introduces computational cost, scaling with the system size and complexity of the potential. Furthermore, numerical differentiation is susceptible to errors arising from finite difference approximations and the inherent limitations of representing continuous functions with discrete data. These errors can accumulate, impacting the accuracy and reliability of simulations, particularly when dealing with complex systems or high-precision requirements. The computational expense associated with differentiation frequently dominates the overall simulation time, hindering the exploration of larger systems or longer timescales.

Direct Force Prediction (DFP) represents a departure from traditional methods of force calculation in molecular dynamics simulations. Instead of determining forces by differentiating the interatomic potential energy function – a process susceptible to numerical instability and computational cost – DFP models are trained to directly output the interatomic force vectors. This approach eliminates the differentiation step entirely, potentially leading to significant efficiency gains, particularly for complex systems or large-scale simulations. The predicted forces are then used directly within Newtonā€™s second law to propagate atomic trajectories, offering a comparable level of accuracy to methods reliant on potential energy surfaces, such as the DPA-3.1-3M model, as demonstrated on benchmarks like matbench-discovery.

Direct force prediction diverges from traditional methods that calculate interatomic forces based on conservative forces derived from potential energy surfaces. This alternative approach allows for the incorporation of non-conservative forces into simulations when physically appropriate, thereby expanding the range of modeled phenomena. Evaluations on the matbench-discovery benchmark demonstrate that direct force prediction achieves accuracy levels comparable to those of established methods such as the DPA-3.1-3M model, validating its efficacy as a simulation technique.

Analysis of a relaxed hexagonal close-packed (HCP) titanium structure reveals a finite-difference force derivative dependent on atomic displacement, which correlates with the resulting phonon band structure along high-symmetry lines in the Brillouin zone.
Analysis of a relaxed hexagonal close-packed (HCP) titanium structure reveals a finite-difference force derivative dependent on atomic displacement, which correlates with the resulting phonon band structure along high-symmetry lines in the Brillouin zone.

The Vibrational Fingerprint: Probing Material Dynamics Through Phonons

A materialā€™s capacity to conduct heat or transmit sound is fundamentally linked to how its atoms vibrate; these vibrations arenā€™t random, but occur at specific frequencies and in defined patterns known as phonon modes. Phonon calculations are designed to map these vibrational characteristics, revealing a materialā€™s intrinsic thermal and acoustic properties. Determining these modes involves solving complex equations that describe the collective atomic movements, effectively creating a ā€˜fingerprintā€™ of how the material responds to external stimuli. Understanding these vibrations is crucial not only for predicting macroscopic behavior-like a materialā€™s melting point or its ability to dampen sound-but also for designing materials with tailored properties for specific applications, ranging from high-efficiency thermoelectric devices to advanced acoustic shielding.

Traditional phonon calculations, essential for characterizing a materialā€™s vibrational behavior and thermal properties, frequently depend on the Finite Difference Method to estimate the necessary derivatives. This approach, while conceptually straightforward, introduces a significant computational burden as it requires evaluating these derivatives multiple times across a vast range of atomic positions and momenta. The resulting demand for processing power scales rapidly with system size and the desired precision of the calculations, effectively limiting the scope of materials that can be accurately modeled with conventional methods. Consequently, researchers are continually exploring alternative strategies to circumvent these computational bottlenecks and enable the efficient investigation of complex materials with intricate vibrational landscapes.

Recent advancements in computational materials science leverage direct force prediction to significantly enhance phonon calculations – the process of determining a materialā€™s vibrational characteristics. This innovative architecture bypasses the computational bottlenecks of traditional methods, which rely on approximating derivatives using techniques like the Finite Difference Method. Evaluations using the SPICE dataset demonstrate competitive accuracy alongside a projected two to three-fold increase in calculation speed when contrasted with conservative modeling approaches. Consequently, researchers gain the capacity to explore a broader spectrum of materials and predict their thermal and acoustic behaviors with greater efficiency, ultimately accelerating the discovery of novel materials tailored for specific applications.

The pursuit of accurate and efficient interatomic potentials, as detailed in this work, echoes a fundamental design principle: elegance stemming from deep understanding. The demonstrated success of rotationally unconstrained graph neural networks – achieving comparable results to equivariant models – highlights how a seemingly simpler approach, when thoughtfully implemented, can rival complexity. This resonates with the idea that true innovation isn’t always about adding layers of sophistication, but about refining the core principles. As Werner Heisenberg observed, ā€œThe very act of observing alters that which is being observed.ā€ This applies to model building; focusing on essential features, rather than attempting to account for every nuance, can yield a more robust and universally applicable system. The research underscores that careful consideration of foundational elements-like the network’s constraints-can dramatically improve performance and broaden applicability in molecular dynamics simulations.

Where to Next?

The demonstration that rotational unconstraint does not necessarily demand a sacrifice in accuracy for machine-learned interatomic potentials feels, at first glance, almostā€¦elegant. For too long, the pursuit of equivariance has been treated as a categorical imperative, a constraint seemingly imposed by the universe itself. This work suggests that, perhaps, clever architectural choices can compensate, allowing for models that are computationally leaner without substantial performance penalties. The field now faces the subtle task of determining when such trade-offs are acceptable-and, crucially, for whom. A faster, slightly less accurate potential might be perfectly adequate for screening millions of materials, but unacceptable for detailed study of a specific, delicate phenomenon.

A pressing concern remains the transferability of these unconstrained models. While benchmarks are valuable, they often reflect a curated reality. True predictive power requires robustness against unseen chemical environments, and a systematic exploration of failure modes is vital. Consistency is empathy; a potential that fails predictably is far more useful than one that produces wildly erratic results. Furthermore, the integration of these potentials with more sophisticated simulation techniques-beyond simple molecular dynamics-presents a considerable challenge.

Ultimately, the success of this approach will not be measured in FLOPS or error metrics alone. It will be judged by its impact on scientific discovery. Beauty does not distract, it guides attention; a simpler, more understandable potential-even if marginally less accurate-can unlock insights that a black box, however powerful, conceals. The pursuit of elegance, it seems, is not merely an aesthetic preference, but a pragmatic necessity.

Original article: https://arxiv.org/pdf/2601.16195.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2026-01-25 10:09